PlatEMO 源码执行的具体过程
ALGORITHM 类
Algorithm类定义在Algorithms文件夹下。在这个目录中,算法根据分类分成了三种:
- 多目标算法:Multi-objecitve optimization
- 单目标算法:Single-objective optimization
- 工具算法:Utility functions
工具算法中包括常见一些【算子】比如遗传算法OperatorGA、做非支配排序的算法、还有计算拥挤距离的算法CrowdingDistance等等
ALGORITHM类是所有的算法的顶级父类,这个类规定和描绘了算法应有的行为。
matlab窗口的左下角可以看出当前类的属性、函数等等
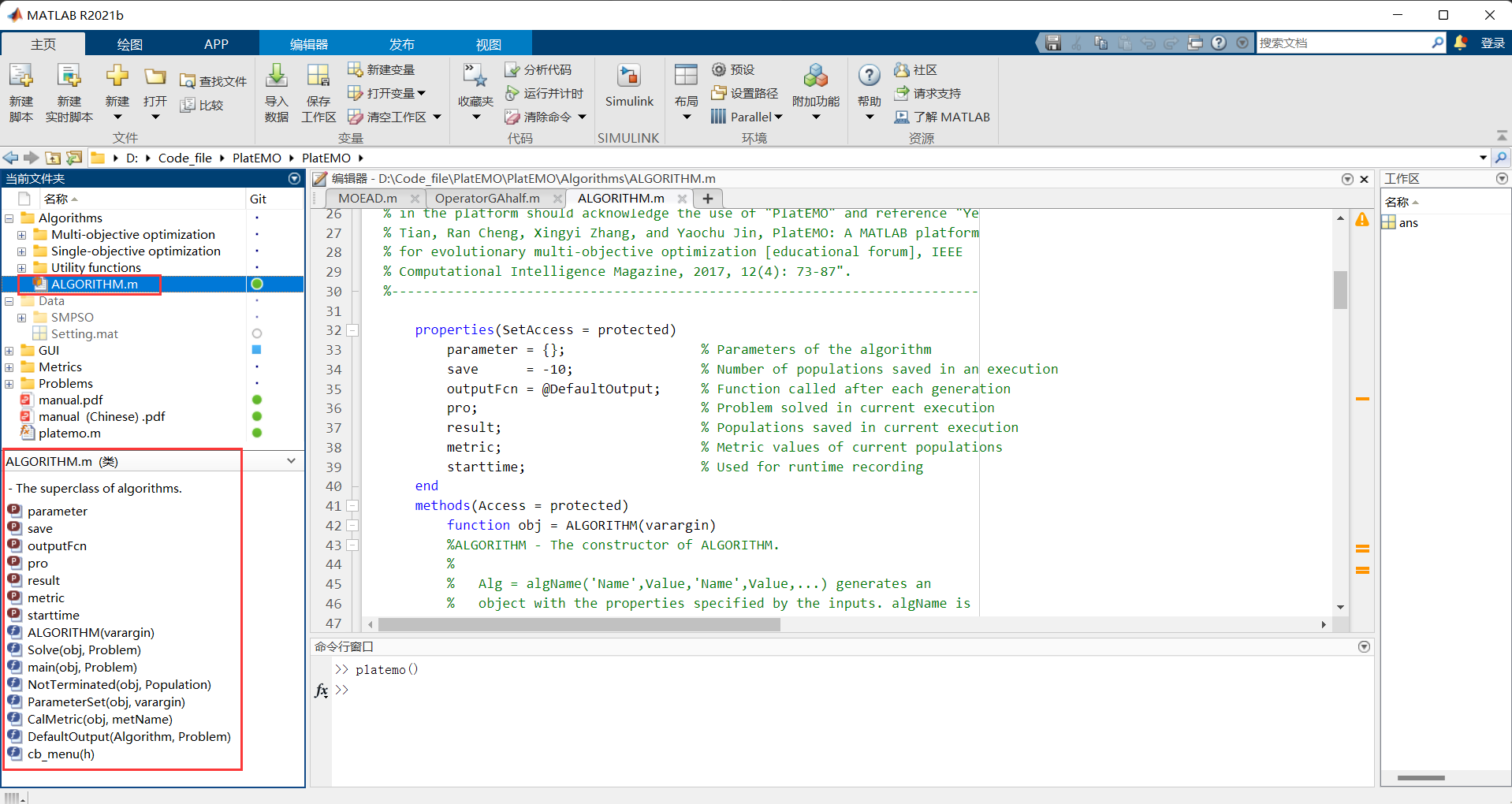
可以发现,算法Algorithm类的实例持有了测试问题Problem类和评价指标Metric类的实例

ParameterSet(obj, varargin)
function varargout = ParameterSet(obj,varargin) % varargin 可以输入任意参数
这个函数有两个输入参数:
obj:表示当前的对象(通常是某种算法对象),该对象包含了一些参数。varargin:这是一个变长参数列表,允许用户传递任意数量的参数。
varargout = varargin;
- 这一行将函数的输出参数
varargout初始化为varargin,即它将以与输入参数相同的值初始化。
specified = ~cellfun(@isempty, obj.parameter);
- 这一行创建一个逻辑数组
specified,它用于指示哪些参数已经在obj.parameter属性中被设置。cellfun函数用于对obj.parameter中的每个元胞进行检查,如果元胞不为空(即参数已设置),则对应的specified元素为true,否则为false。(cellfun(func, C)将函数 func 应用于元胞数组 C 的每个元胞的内容, A(i) = func(C{i}))
varargout(specified) = obj.parameter(specified);
- 这一行将
obj.parameter中已经设置的参数值复制到varargout中相应位置。这意味着如果参数已经在obj.parameter属性中设置,那么它们的默认值将被替换为obj.parameter中的值,否则将保留用户传递的值。 - 最后,这个函数返回
varargout,其中包含了经过处理的参数值。这允许用户在不指定参数值时使用默认值,或者在需要时指定特定的参数值。
Solve
function Solve(obj,Problem)
%Solve - Use the algorithm to solve a problem.
%
% obj.Solve(Pro) uses the algorithm to solve a problem, where Pro
% is a PROBLEM object.
%
% In terms of the default obj.outputFcn, the result will be
% displayed when obj.save = 0 and saved when obj.save > 0.
%
% Example:
% Algorithm.Solve(Problem)
try
obj.result = {};
obj.metric = struct('runtime',0);
obj.pro = Problem;
obj.pro.FE = 0;
addpath(fileparts(which(class(obj))));
addpath(fileparts(which(class(obj.pro))));
obj.starttime = tic;
obj.main(obj.pro);
catch err
if ~strcmp(err.identifier,'PlatEMO:Termination')
rethrow(err);
end
end
end
function Solve(obj,Problem)
- 该函数用于使用 PlatEMO 框架中的特定算法解决给定问题
try
try:这是一个错误处理块的开始,用于捕获可能出现的异常情况。
obj.result = {};
obj.result = {}:将 PlatEMO 算法对象的 result 属性初始化为空单元数组。
obj.metric = struct('runtime',0);
obj.metric = struct('runtime', 0):将 PlatEMO 算法对象的 metric 属性初始化为包含一个名为 runtime 的字段,其值为 0 的结构体。
obj.pro = Problem;
obj.pro.FE = 0;
obj.pro = Problem:将 PlatEMO 算法对象的 pro 属性设置为传递给函数的 Problem 参数,以表示要解决的问题。obj.pro.FE = 0:将obj.pro对象的 FE 属性(可能代表 Function Evaluations)设置为 0。
addpath(fileparts(which(class(obj))));
addpath(fileparts(which(class(obj.pro))));
addpath(fileparts(which(class(obj))):将当前对象所属类的文件所在目录添加到 MATLAB 的搜索路径,以确保能够访问与当前对象相关的类文件。addpath(fileparts(which(class(obj.pro))):将问题对象 Problem 所属类的文件所在目录添加到 MATLAB 的搜索路径。which(class(obj))获取了当前对象 obj 所属类的完整路径,这是因为 MATLAB 中的类通常存储在独立的类文件中,而该代码会返回类文件的完整路径。fileparts()函数用于获取路径的父目录,也就是去掉文件名的部分。addpath()函数将这个父目录添加到 MATLAB 的搜索路径中,以便 MATLAB 可以在运行时找到这个类的定义和相关函数。
obj.starttime = tic;
obj.main(obj.pro); % 这里的每个算法中都是对 Algorithm 中的 main 重写过得
obj.main(obj.pro):启动计时器(tic),然后调用 PlatEMO 算法对象的 main 方法,并传递 obj.pro 作为参数,以启动算法的主要求解过程。
catch err
if ~strcmp(err.identifier,'PlatEMO:Termination')
rethrow(err);
end
end
catch err:捕获异常,并将异常信息存储在 err 变量中。if ~strcmp(err.identifier,'PlatEMO:Termination'):检查异常的标识符,如果不等于 ‘PlatEMO:Termination’,则执行以下操作。rethrow(err):重新引发捕获的异常,将异常传递给调用者。
main
其他算法在继承 ALGORITHM 类时均会重写 main 方法,如下 MOEAD 算法
function main(obj,Problem)
%main - The main function of the algorithm.
%
% This function is expected to be implemented in each subclass of
% ALGORITHM, which is usually called by ALGORITHM.Solve.
end

NotTerminated
function nofinish = NotTerminated(obj,Population)
%NotTerminated - The function called after each generation of the
%execution.
%
% obj.NotTerminated(P) stores the population P as the result of
% the current execution, and returns true if the algorithm should
% be terminated, i.e., the number of function evaluations or
% runtime exceeds.
%
% obj.outputFcn is called here, whose runtime will not be counted
% in the runtime of current execution.
%
% Example:
% while Algorithm.NotTerminated(Population)
% ... ...
% end
obj.metric.runtime = obj.metric.runtime + toc(obj.starttime);
if obj.pro.maxRuntime < inf
obj.pro.maxFE = obj.pro.FE*obj.pro.maxRuntime/obj.metric.runtime;
end
num = max(1,abs(obj.save));
index = max(1,min(min(num,size(obj.result,1)+1),ceil(num*obj.pro.FE/obj.pro.maxFE)));
obj.result(index,:) = {obj.pro.FE,Population};
drawnow('limitrate');
obj.outputFcn(obj,obj.pro);
nofinish = obj.pro.FE < obj.pro.maxFE;
assert(nofinish,'PlatEMO:Termination','');
obj.starttime = tic;
end
- 第24行中,算法将Population放入了result属性中
- 第26行中,算法调用了outputFcn。实际上outputFcn这个函数在每一代结束后被调用
- 在第27行,通过比较FE和设置的最大FE,判断算法是否应该结束。如果应该结束的话通过第28行的assert抛出一个异常来强制结束,PlatEMO是非常公平的!
function nofinish = NotTerminated(obj,Population)
- 用于算法的终止条件检测和结果记录
obj.metric.runtime = obj.metric.runtime + toc;
obj.metric.runtime = obj.metric.runtime + toc;:用于记录算法的运行时间。toc 函数返回自上一次调用 tic 函数以来经过的时间,这样就可以累积算法的总运行时间。运行时间记录在obj.metric.runtime属性中。
if obj.pro.maxRuntime < inf
obj.pro.maxFE = obj.pro.FE*obj.pro.maxRuntime/obj.metric.runtime;
end
-
if obj.pro.maxRuntime < inf:这是一个条件语句,它检查是否设置了算法的最大运行时间。如果obj.pro.maxRuntime小于正无穷(inf),表示设置了最大运行时间,即算法运行时间受到限制。 -
obj.pro.maxFE = obj.pro.FE * obj.pro.maxRuntime / obj.metric.runtime:这行代码计算了在规定的最大运行时间内允许的函数评估次数(FE)。它根据已经执行的函数评估次数(obj.pro.FE)、设置的最大运行时间(obj.pro.maxRuntime)以及当前的累积运行时间(obj.metric.runtime)来确定。
num = max(1,abs(obj.save));
num = max(1, abs(obj.save)):这行代码计算了要保存的种群数量。obj.save 表示设置的保存种群的数量,但如果它小于1,则至少保存一个种群。
index = max(1,min(min(num,size(obj.result,1)+1),ceil(num*obj.pro.FE/obj.pro.maxFE)));
- 代码用于确定要保存种群的位置(索引)。它考虑了要保存的种群数量(
num)、已经保存的种群数目(size(obj.result, 1))、以及函数评估次数和允许的函数评估次数的比例。
obj.result(index,:) = {obj.pro.FE,Population};
obj.result(index, :) = {obj.pro.FE, Population}:这行代码将当前种群(Population)和对应的函数评估次数(obj.pro.FE)存储在obj.result中的特定位置(由index确定)。
drawnow('limitrate');
drawnow('limitrate');:这是一个MATLAB函数,用于更新图形界面,以确保结果的及时显示。
obj.outputFcn(obj,obj.pro);
- 代码调用
obj.outputFcn函数,(默认调用的是 DefaultOutput,因为 outputFcn = @DefaultOutput)该函数在每一代后调用,通常用于显示结果或记录数据。函数的参数包括obj(算法对象)和obj.pro(当前执行的问题对象)。
nofinish = obj.pro.FE < obj.pro.maxFE;
- 代码检查算法是否应该终止。它比较已经执行的函数评估次数(obj.pro.FE)和允许的最大函数评估次数(obj.pro.maxFE)。如果已经执行的次数小于最大次数,nofinish 被设置为true,表示算法不应终止,否则被设置为false,表示算法应该终止。
assert(nofinish,'PlatEMO:Termination','');
- 断言语句,用于检查nofinish是否为true。如果nofinish不为true,则触发一个异常,异常的标识是 ‘PlatEMO:Termination’,并且异常消息为空字符串。这意味着如果算法应该终止(nofinish为false),则会引发一个异常,可能会中止算法的执行。
tic;
- 最后,代码重新启动计时器,以准备下一代的运行时间记录。
outputFcn/DefaultOutput
function DefaultOutput(Algorithm,Problem)
% The default output function of ALGORITHM
clc; fprintf('%s on %d-objective %d-variable %s (%6.2f%%), %.2fs passed...\n',class(Algorithm),Problem.M,Problem.D,class(Problem),Problem.FE/Problem.maxFE*100,Algorithm.metric.runtime);
if Problem.FE >= Problem.maxFE
if Algorithm.save < 0
if Problem.M > 1
Population = Algorithm.result{end};
if length(Population) >= size(Problem.optimum,1); name = 'HV'; else; name = 'IGD'; end
value = Algorithm.CalMetric(name);
figure('NumberTitle','off','Name',sprintf('%s : %.4e Runtime : %.2fs',name,value(end),Algorithm.CalMetric('runtime')));
title(sprintf('%s on %s',class(Algorithm),class(Problem)),'Interpreter','none');
top = uimenu(gcf,'Label','Data source');
g = uimenu(top,'Label','Population (obj.)','CallBack',{@(h,~,Pro,P)eval('Draw(gca);Pro.DrawObj(P);cb_menu(h);'),Problem,Population});
uimenu(top,'Label','Population (dec.)','CallBack',{@(h,~,Pro,P)eval('Draw(gca);Pro.DrawDec(P);cb_menu(h);'),Problem,Population});
uimenu(top,'Label','True Pareto front','CallBack',{@(h,~,P)eval('Draw(gca);Draw(P,{''\it f\rm_1'',''\it f\rm_2'',''\it f\rm_3''});cb_menu(h);'),Problem.optimum});
cellfun(@(s)uimenu(top,'Label',s,'CallBack',{@(h,~,A)eval('Draw(gca);Draw(A.CalMetric(h.Label),''-k.'',''LineWidth'',1.5,''MarkerSize'',10,{''Number of function evaluations'',strrep(h.Label,''_'','' ''),[]});cb_menu(h);'),Algorithm}),{'IGD','HV','GD','Feasible_rate'});
set(top.Children(4),'Separator','on');
g.Callback{1}(g,[],Problem,Population);
else
best = Algorithm.CalMetric('Min_value');
if isempty(best); best = nan; end
figure('NumberTitle','off','Name',sprintf('Min value : %.4e Runtime : %.2fs',best(end),Algorithm.CalMetric('runtime')));
title(sprintf('%s on %s',class(Algorithm),class(Problem)),'Interpreter','none');
top = uimenu(gcf,'Label','Data source');
uimenu(top,'Label','Population (dec.)','CallBack',{@(h,~,Pro,P)eval('Draw(gca);Pro.DrawDec(P);cb_menu(h);'),Problem,Algorithm.result{end}});
cellfun(@(s)uimenu(top,'Label',s,'CallBack',{@(h,~,A)eval('Draw(gca);Draw(A.CalMetric(h.Label),''-k.'',''LineWidth'',1.5,''MarkerSize'',10,{''Number of function evaluations'',strrep(h.Label,''_'','' ''),[]});cb_menu(h);'),Algorithm}),{'Min_value','Feasible_rate'});
set(top.Children(2),'Separator','on');
top.Children(2).Callback{1}(top.Children(2),[],Algorithm);
end
elseif Algorithm.save > 0
folder = fullfile('Data',class(Algorithm));
[~,~] = mkdir(folder);
file = fullfile(folder,sprintf('%s_%s_M%d_D%d_',class(Algorithm),class(Problem),Problem.M,Problem.D));
runNo = 1;
while exist([file,num2str(runNo),'.mat'],'file') == 2
runNo = runNo + 1;
end
result = Algorithm.result;
metric = Algorithm.metric;
save([file,num2str(runNo),'.mat'],'result','metric');
end
end
end
function DefaultOutput(Algorithm,Problem)
在 PlatEMO 中,调用 obj.outputFcn(obj, obj.pro) 实际上是调用默认的输出函数 DefaultOutput。这是因为在默认情况下,outputFcn 属性被设置为 @DefaultOutput,它是一个函数句柄,指向默认的输出函数。
所以,当 obj.outputFcn(obj, obj.pro) 被调用时,它实际上是在执行 DefaultOutput(obj, obj.pro),这会触发默认输出函数的操作。默认输出函数通常用于在每一代或特定时间点生成一些基本的输出,如显示进度信息、记录基本结果等。
- 显示算法进度信息:输出算法的名称、目标数、变量数、问题的名称、已经执行的函数评估次数、算法运行时间等信息。这些信息可帮助用户了解算法的执行情况。
- 检查算法是否达到最大函数评估次数(Problem.FE >= Problem.maxFE):如果算法已经执行了足够的函数评估次数,就会执行以下操作:
- 检查是否需要保存种群数据(Algorithm.save < 0):如果需要保存种群数据,就会执行以下操作:
- 如果问题具有多个目标,将生成图表显示种群的指标值(如 Hypervolume 和 Inverted Generational Distance)随着函数评估次数的变化情况。如果已经保存了足够多的种群(数量达到问题 Pareto 前沿的大小),则使用 Hypervolume,否则使用 Inverted Generational Distance。
- 生成图表以显示种群的目标值、决策变量值以及问题的真实 Pareto 前沿(如果可用)。
- 如果问题只有一个目标,将生成图表显示最小值和可行性比例随着函数评估次数的变化情况。
- 如果需要保存种群数据(Algorithm.save > 0):将种群数据和性能指标保存到文件中。文件名包括算法名称、问题名称、目标数和变量数,以及一个唯一的运行编号。
- 检查是否需要保存种群数据(Algorithm.save < 0):如果需要保存种群数据,就会执行以下操作:
举例说明
在ALGORITHM类中,这个类并没有被实现,需要在子类中实现。以SMPSO算法为例。算法主要有这样的几个部分:
- 需要继承ALGORITHM类
- 需要通过打标签的形式声明当前的算法属于的类型,比如SMPSO属于多目标的、约束类型,支持的编码方式有实数、二进制、排列等
- 在子类中实现main函数
- 在while循环中通过NotTerminated进行控制循环
classdef MOEAD < ALGORITHM
% <multi/many> <real/integer/label/binary/permutation>
%------------------------------- Reference --------------------------------
% Q. Zhang and H. Li, MOEA/D: A multiobjective evolutionary algorithm based
% on decomposition, IEEE Transactions on Evolutionary Computation, 2007,
% 11(6): 712-731.
%--------------------------------------------------------------------------
methods
function main(Algorithm,Problem)
%% ..... 省略逻辑
%% Optimization
while Algorithm.NotTerminated(Population)
%% ..... 省略逻辑
end
end
end
end
PROBLEM 类
Initialization
一个算法需要在该测试问题指定的决策变量空间中初始化,想当然地,初始化种群的任务应该交给Problem类实现:
如果测试问题没有重写Initialization方法,会自动走初始化实数型,大小为100的种群的逻辑。种群初始化会保证在上下界范围之内。
function Population = Initialization(obj,N)
%Initialization - Generate multiple initial solutions.
%
% P = obj.Initialization() randomly generates the decision
% variables of obj.N solutions and returns the SOLUTION objects.
%
% P = obj.Initialization(N) generates N solutions.
%
% This function is usually called at the beginning of algorithms.
%
% Example:
% Population = Problem.Initialization()
if nargin < 2
N = obj.N;
end
PopDec = zeros(N,obj.D);
Type = arrayfun(@(i)find(obj.encoding==i),1:5,'UniformOutput',false);
if ~isempty(Type{1}) % Real variables
PopDec(:,Type{1}) = unifrnd(repmat(obj.lower(Type{1}),N,1),repmat(obj.upper(Type{1}),N,1));
end
if ~isempty(Type{2}) % Integer variables
PopDec(:,Type{2}) = round(unifrnd(repmat(obj.lower(Type{2}),N,1),repmat(obj.upper(Type{2}),N,1)));
end
if ~isempty(Type{3}) % Label variables
PopDec(:,Type{3}) = round(unifrnd(repmat(obj.lower(Type{3}),N,1),repmat(obj.upper(Type{3}),N,1)));
end
if ~isempty(Type{4}) % Binary variables
PopDec(:,Type{4}) = logical(randi([0,1],N,length(Type{4})));
end
if ~isempty(Type{5}) % Permutation variables
[~,PopDec(:,Type{5})] = sort(rand(N,length(Type{5})),2);
end
Population = obj.Evaluation(PopDec);
end
function Population = Initialization(obj,N)
- 用于初始种群,其中
obj是当前算法对象,N是要生成的初始解的数量。
if nargin < 2
N = obj.N;
end
- 首先,检查函数输入参数的数量,如果用户没有指定生成解的数量N,则使用默认值obj.N,obj.N通常是算法对象中的一个属性,表示默认生成解的数量。
PopDec = zeros(N,obj.D);
- 创建一个大小为
N行obj.D列的零矩阵PopDec,其中N表示生成的解的数量,obj.D表示决策变量的维度。这个矩阵用于存储生成的解的决策变量。
Type = arrayfun(@(i)find(obj.encoding==i),1:5,'UniformOutput',false);
-
根据
obj.encoding属性中的信息,根据不同的编码类型(Real、Integer、Label、Binary、Permutation),对PopDec中的相应列进行初始化。这是根据不同类型的变量生成初始值的步骤。 -
arrayfun是MATLAB中的一个函数,用于将给定函数应用于数组的每个元素,并返回结果。 -
@(i)find(obj.encoding==i)是一个匿名函数,它接受一个参数i,然后在obj.encoding中查找等于i的元素的索引。这将返回一个包含这些索引的数组。 -
1:5创建一个包含1到5的整数数组,表示要查找的值。(1(实数)、2(整数)、3(标签)、4(二进制数)或 5(序列编号)) -
'UniformOutput', false是arrayfun函数的选项,指示函数的输出是否应该具有一致的大小。在这里,false表示输出数组的大小可以不一致。 -
因此,这行代码的作用是创建一个名为
Type的数组,其中包含了obj.encoding中1到5这些值的索引。每个索引将分别对应于1到5这些值在obj.encoding中的位置。Type数组的长度可能因为在obj.encoding中找到的不同值而不同。这种操作通常用于构建一个索引数组,以便在后续的操作中可以根据Type中的索引值访问obj.encoding中的对应元素。 -
最后,调用
obj.Evaluation方法,将生成的PopDec矩阵传递给该方法,以获得相应的目标值和约束值,从而构建完整的种群对象。生成的种群对象Population包含了初始解的决策变量和相应的目标值。
if ~isempty(Type{1}) % Real variables
PopDec(:,Type{1}) = unifrnd(repmat(obj.lower(Type{1}),N,1),repmat(obj.upper(Type{1}),N,1));
end
-
实数变量(Real variables):
- 首先,检查Type{1}是否为空。Type{1}包含了实数变量的索引或标识。
- 如果不为空,表示存在实数变量,那么执行以下操作:
- 使用
repmat函数创建大小为N行1列的矩阵,其中每行都包含了obj.lower(Type{1})和obj.upper(Type{1})中相应的下界和上界值。 - 使用
unifrnd函数生成一个大小为N行1列的随机矩阵,其中的随机数在对应的下界和上界范围内。 - 将生成的随机数赋值给
PopDec矩阵的列,这些列对应于实数变量的索引。
- 使用
if ~isempty(Type{2}) % Integer variables
PopDec(:,Type{2}) = round(unifrnd(repmat(obj.lower(Type{2}),N,1),repmat(obj.upper(Type{2}),N,1)));
end
- 整数变量(Integer variables):
- 同样,检查
Type{2}是否为空,其中包含了整数变量的索引或标识。 - 如果不为空,表示存在整数变量,那么执行以下操作:
- 使用repmat函数创建大小为N行 * 1列的矩阵,其中每行都包含了obj.lower(Type{2})和obj.upper(Type{2})中相应的下界和上界值。
- 使用unifrnd函数生成一个大小为N行 1列的随机矩阵,其中的随机数在对应的下界和上界范围内。
- 使用round函数对生成的随机数取整,以确保它们是整数。
- 将生成的整数值赋值给PopDec矩阵的列,这些列对应于整数变量的索引。
- 同样,检查
if ~isempty(Type{3}) % Label variables
PopDec(:,Type{3}) = round(unifrnd(repmat(obj.lower(Type{3}),N,1),repmat(obj.upper(Type{3}),N,1)));
end
-
标签变量(Label variables):
- 同样,检查Type{3}是否为空,其中包含了标签变量的索引或标识。
- 如果不为空,表示存在标签变量,那么执行以下操作:
- 使用repmat函数创建大小为N行 * 1列的矩阵,其中每行都包含了obj.lower(Type{3})和obj.upper(Type{3})中相应的下界和上界值。
- 使用unifrnd函数生成一个大小为N行 * 1列的随机矩阵,其中的随机数在对应的下界和上界范围内。
- 使用round函数对生成的随机数取整,以确保它们是整数。
- 将生成的整数值赋值给PopDec矩阵的列,这些列对应于标签变量的索引。
if ~isempty(Type{4}) % Binary variables
PopDec(:,Type{4}) = logical(randi([0,1],N,length(Type{4})));
end
-
二进制变量(Binary variables):
- 同样,检查Type{4}是否为空,其中包含了二进制变量的索引或标识。
- 如果不为空,表示存在二进制变量,那么执行以下操作:
- 使用
randi函数生成一个大小为N行length(Type{4})列的逻辑矩阵,其中每个元素是0或1,表示二进制值。 - 将生成的二进制值矩阵赋值给PopDec矩阵的列,这些列对应于二进制变量的索引。
- 使用
if ~isempty(Type{5}) % Permutation variables
[~,PopDec(:,Type{5})] = sort(rand(N,length(Type{5})),2);
end
- 排列变量(Permutation variables):
- 最后,检查Type{5}是否为空,其中包含了排列变量的索引或标识。
- 如果不为空,表示存在排列变量,那么执行以下操作:
- 使用rand函数生成一个大小为N行 length(Type{5})列的随机矩阵,其中的随机数在0到1之间。
- 使用sort函数对每行的随机数进行排序,生成排列的索引。
- 将生成的排列索引矩阵赋值给PopDec矩阵的列,这些列对应于排列变量的索引。
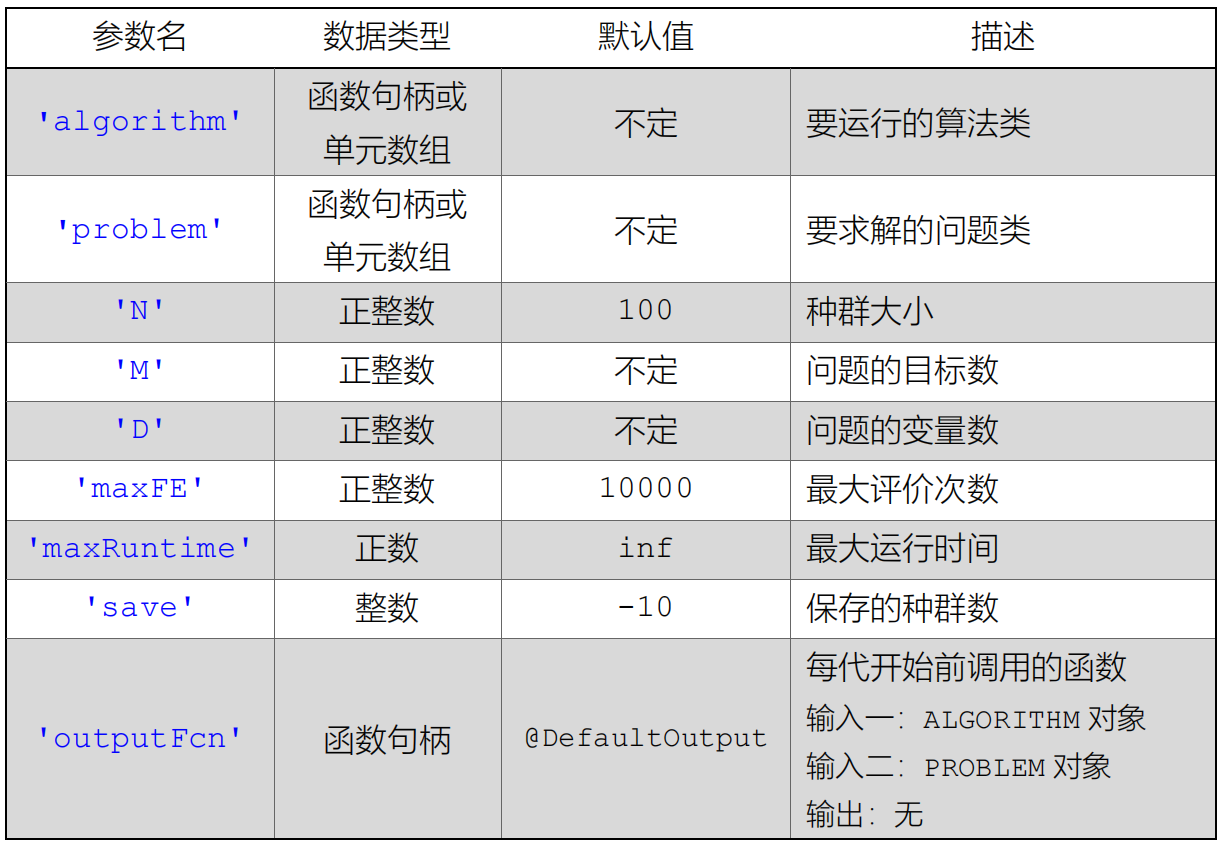
默认的Initialization方法根据当前的编码方式和种群大小进行初始化。Problem类中默认的信息如下:
properties
N = 100; % Population size
maxFE = 10000; % Maximum number of function evaluations
FE = 0; % Number of consumed function evaluations
end
properties(SetAccess = protected)
M; % Number of objectives
D; % Number of decision variables
maxRuntime = inf; % maximum runtime (in second)
encoding = 1; % Encoding scheme of each decision variable (1.real 2.integer 3.label 4.binary 5.permutation)
lower = 0; % Lower bound of each decision variable
upper = 1; % Upper bound of each decision variable
optimum; % Optimal values of the problem
PF; % Image of Pareto front
parameter = {}; % Other parameters of the problem
end
Setting
Setting在父类中没有被重写,需要各个测试问题进行覆写。
function Setting(obj)
%Setting - Default settings of the problem.
%
% This function is expected to be implemented in each subclass of
% PROBLEM, which is usually called by the constructor.
end
Evaluation
function Population = Evaluation(obj,varargin)
%Evaluation - Evaluate multiple solutions.
%
% P = obj.Evaluation(Dec) returns the SOLUTION objects based on
% the decision variables Dec. The objective values and constraint
% violations of the solutions are calculated automatically, and
% obj.FE is increased accordingly.
%
% P = obj.Evaluation(Dec,Add) also sets the additional properties
% (e.g., velocity) of solutions.
%
% This function is usually called after generating new solutions.
%
% Example:
% Population = Problem.Evaluation(PopDec)
% Population = Problem.Evaluation(PopDec,PopVel)
PopDec = obj.CalDec(varargin{1});
PopObj = obj.CalObj(PopDec);
PopCon = obj.CalCon(PopDec);
Population = SOLUTION(PopDec,PopObj,PopCon,varargin{2:end});
obj.FE = obj.FE + length(Population);
end
function Population = Evaluation(obj,varargin)
PopDec = obj.CalDec(varargin{1}); % 处理异常处理(包括超出上下界的数据)
PopObj = obj.CalObj(PopDec); % 计算决策变量的目标值
PopCon = obj.CalCon(PopDec); % 获取约束违反值
Population = SOLUTION(PopDec,PopObj,PopCon,varargin{2:end}); % 将每个解转为 SOLUTION 对象
obj.FE = obj.FE + length(Population); % 记录评估次数
这个函数的主要目的是评估给定的决策变量,并计算每个解的目标值(objective values)和约束违反情况(constraint violations)。以下是函数的主要操作步骤:
首先,从输入参数varargin中提取决策变量PopDec,通过调用CalDec方法来将其提取出来。CalDec方法的作用是根据输入的决策变量计算问题相关的决策变量。
使用提取出的PopDec,调用CalObj方法来计算每个解的目标值PopObj。CalObj方法的作用是根据决策变量计算问题相关的目标值。
同样使用PopDec,调用CalCon方法来计算每个解的约束违反情况PopCon。CalCon方法的作用是根据决策变量计算问题相关的约束情况。
创建SOLUTION对象,将决策变量PopDec、目标值PopObj、约束情况PopCon以及可能的其他属性(如果在输入中提供了)传递给SOLUTION构造函数。SOLUTION对象通常用于表示一个解,包含了解的决策变量、目标值、约束情况等信息。
最后,更新问题对象obj中的FE属性,表示已经评估了多少个解。通常,每次评估一个解,FE属性就会增加一个。
这个函数通常在生成新的解后被调用,以计算这些解的目标值和约束情况。评估后的结果以SOLUTION对象的形式返回,以便进行后续的处理和优化。
CalDec
function PopDec = CalDec(obj,PopDec)
%CalDec - Repair multiple invalid solutions.
%
% Dec = obj.CalDec(Dec) repairs the invalid (not infeasible)
% decision variables in Dec.
%
% An invalid solution indicates that it is out of the decision
% space, while an infeasible solution indicates that it does not
% satisfy all the constraints.
%
% This function is usually called by PROBLEM.Evaluation.
%
% Example:
% PopDec = Problem.CalDec(PopDec)
Type = arrayfun(@(i)find(obj.encoding==i),1:5,'UniformOutput',false);
index = [Type{1:3}];
if ~isempty(index)
PopDec(:,index) = max(min(PopDec(:,index),repmat(obj.upper(index),size(PopDec,1),1)),repmat(obj.lower(index),size(PopDec,1),1));
end
index = [Type{2:5}];
if ~isempty(index)
PopDec(:,index) = round(PopDec(:,index));
end
end
function PopDec = CalDec(obj,PopDec)
- 用于修复多个无效的解(invalid solutions)中的决策变量(一个无效解表示它的决策变量超出了合法决策空间的范围)。其中obj表示当前问题对象,PopDec是包含多个解的决策变量矩阵。
Type = arrayfun(@(i)find(obj.encoding==i),1:5,'UniformOutput',false);
- 首先,从问题对象obj中获取包含不同类型决策变量的索引,这些索引存储在Type单元格数组中。这些类型可以包括实数变量、整数变量、标签变量等。
index = [Type{1:3}];
- 这行代码创建一个包含实数变量、整数变量和标签变量的索引的数组
index。这些索引是从Type单元格数组中提取的。
if ~isempty(index)
PopDec(:,index) = max(min(PopDec(:,index),repmat(obj.upper(index),size(PopDec,1),1)),repmat(obj.lower(index),size(PopDec,1),1));
end
if ~isempty(index)这行代码检查index数组是否不为空。如果不为空,表示存在需要处理的实数变量、整数变量和标签变量。PopDec(:,index)选择PopDec矩阵中的所有行和index中指定的列。这表示要处理PopDec中与index列对应的决策变量。repmat(obj.upper(index), size(PopDec, 1), 1)创建一个大小与PopDec相同的矩阵,其中每行都包含了obj.upper(index)中对应的上界值。同样,repmat(obj.lower(index), size(PopDec, 1), 1)创建一个包含下界值的矩阵。min(PopDec(:, index), ...)将PopDec中的决策变量值与上界值进行比较,返回每个元素中的最小值。这将确保决策变量值不会超过上界。max(..., repmat(obj.lower(index), size(PopDec, 1), 1))再次将上一步得到的结果与下界值进行比较,返回每个元素中的最大值。这将确保决策变量值不会低于下界。
index = [Type{2:5}];
index = [Type{2:5}];这行代码创建一个包含整数变量、标签变量、二进制变量和排列变量的索引的数组index。这些索引是从Type单元格数组中提取的。
if ~isempty(index)
PopDec(:,index) = round(PopDec(:,index));
end
- 确保整数变量、标签变量、二进制变量和排列变量的值都是整数,利用
round来实现四舍五入
CalObj
function PopObj = CalObj(obj,PopDec)
%CalObj - Calculate the objective values of multiple solutions.
%
% Obj = obj.CalObj(Dec) returns the objective values of Dec.
%
% This function is usually called by PROBLEM.Evaluation.
%
% Example:
% PopObj = Problem.CalObj(PopDec)
PopObj = zeros(size(PopDec,1),1);
end
function PopObj = CalObj(obj,PopDec)
PopDec 为决策变量矩阵,通过 CalObj 方法中的计算方法,得到目标值,存储在 PopObj 中
CalCon
function PopCon = CalCon(obj,PopDec)
%CalCon - Calculate the constraint violations of multiple solutions.
%
% Con = obj.CalCon(Dec) returns the constraint violations of Dec.
%
% This function is usually called by PROBLEM.Evaluation.
%
% Example:
% PopCon = Problem.CalCon(PopDec)
PopCon = zeros(size(PopDec,1),1);
end
function PopCon = CalCon(obj,PopDec)
根据给定的决策变量矩阵PopDec计算每个解的约束违反值,并将这些值存储在PopCon中。
在代码中的实际计算部分,只是简单地创建了一个大小与解的数量相同的列向量PopCon,并将其所有元素初始化为零。这意味着在这个特定问题中,所有的解都是满足约束的,没有任何约束违反。
DrawObj
function DrawObj(obj,Population)
%DrawObj - Display a population in the objective space.
%
% obj.DrawObj(P) displays the objective values of population P.
%
% This function is usually called by the GUI.
%
% Example:
% Problem.DrawObj(Population)
ax = Draw(Population.objs,{'\it f\rm_1','\it f\rm_2','\it f\rm_3'});
if ~isempty(obj.PF)
if ~iscell(obj.PF)
if obj.M == 2
plot(ax,obj.PF(:,1),obj.PF(:,2),'-k','LineWidth',1);
elseif obj.M == 3
plot3(ax,obj.PF(:,1),obj.PF(:,2),obj.PF(:,3),'-k','LineWidth',1);
end
else
if obj.M == 2
surf(ax,obj.PF{1},obj.PF{2},obj.PF{3},'EdgeColor','none','FaceColor',[.85 .85 .85]);
elseif obj.M == 3
surf(ax,obj.PF{1},obj.PF{2},obj.PF{3},'EdgeColor',[.8 .8 .8],'FaceColor','none');
end
set(ax,'Children',ax.Children(flip(1:end)));
end
elseif size(obj.optimum,1) > 1 && obj.M < 4
if obj.M == 2
plot(ax,obj.optimum(:,1),obj.optimum(:,2),'.k');
elseif obj.M == 3
plot3(ax,obj.optimum(:,1),obj.optimum(:,2),obj.optimum(:,3),'.k');
end
end
end
end
这部分逻辑概括起来就是需要根据当前种群,绘制在目标空间中的位置。
当种群不为空时,交给Draw进行绘制。Draw在GUI文件夹中,专门处理绘制的函数。有兴趣的大家可以去看看,逻辑稍微有点复杂,大家可以通过debug的形式去分析。
Draw在这里传入两个参数,第一个参数是种群的目标函数值,第二个是坐标轴的字符串元胞数组。
if ~isempty(Population)
ax = Draw(Population.objs,{'\it f\rm_1','\it f\rm_2','\it f\rm_3'});
else
在代码的第13行,判断PF是否为空。PF是什么呢?PF在PlatEMO中通俗理解就是可行域,而不是帕累托前沿。
首先PF这个属性在测试问题的构造函数中已经被初始化了:
function obj = PROBLEM(varargin)
isStr = find(cellfun(@ischar,varargin(1:end-1))&~cellfun(@isempty,varargin(2:end)));
for i = isStr(ismember(varargin(isStr),{'N','M','D','maxFE','parameter'}))
obj.(varargin{i}) = varargin{i+1};
end
obj.Setting();
obj.optimum = obj.GetOptimum(10000);
obj.PF = obj.GetPF();
end
GetPF方法需要在子类中实现,我们以MW11问题为例:

MW11有四个约束函数,当四个约束函数都满足时,才是可行域。对比一下左边的定义和右边的实现,你就知道为什么我说GetPF相当于是获取函数在目标空间中的可行域了。
在获取目标空间的可行域之后,DrawObj就会根据目标的数量进行绘制。
所以DrawObj的逻辑主要分成两个方面:
- 通过Draw在目标空间中绘制Population.obj
- 首先通过GetPF获取可行域,然后通过plot绘制可行域
SOLUTION类
一般认为算法使用一个测试问题进行一次函数评估之后就需要+1次函数评估次数(FE),以 MW11 为例,我们并不能看到有任何类似于+1的实现:
function PopObj = CalObj(obj,X)
g = 1 + sum(2*(X(:,obj.M:end) + (X(:,obj.M-1:end-1) - 0.5).^2 - 1).^2,2);
PopObj(:,1) = g.*X(:,1)*sqrt(1.9999);
PopObj(:,2) = g.*sqrt(2 - (PopObj(:,1)./g).^2);
end
在 PlatEMO 中,对应的实现藏在 Solution 类中。
Solution 在 PlatEMO 中表示单个个体,而 Population 就是 Solution 的矩阵。比如具有 100 个个体的种群就是 100 ? 1 ? S o l u t i o n 100 * 1 ~ Solution 100?1?Solution。

Solution中没有重要的函数,其函数都是用于获取属性的。比如我们通过Population.objs
function value = objs(obj)
%objs - Get the matrix of objective values of a population.
%
% Obj = obj.objs returns the matrix of objective values of
% multiple solutions obj.
value = cat(1,obj.obj);
end
下面具体看下如何实现的
构造函数:function obj = SOLUTION(PopDec,PopObj,PopCon,PopAdd)
obj(1,size(PopDec,1)) = SOLUTION;
产生大小为 1 × size(PopDec,1) 的 SOLUTION 类
for i = 1 : length(obj)
obj(i).dec = PopDec(i,:);
obj(i).obj = PopObj(i,:);
obj(i).con = PopCon(i,:);
end
if nargin > 3
for i = 1 : length(obj)
obj(i).add = PopAdd(i,:);
end
end
为每个类赋值,即可完成。
References
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!