scikit-learn实现线性回归

要学习scikit-learn,我们必须要到scikit-clearn的官网中去查看公式和原理
scikit-learn 官网
scikit-learn 中文社区
进入官网一以后我们找到回归，然后再有监督学习中找到线性模型

scikit-learn实现简单的线性回归

公式：

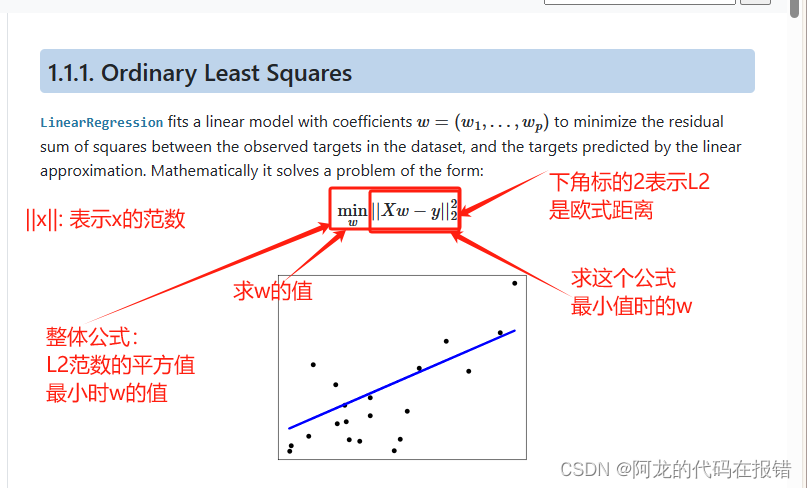
L2范数是指向量中每个元素的平方和的平方根。在数学中，L2范数也称为欧几里得范数，通常用 $||x|{|}_2$ 表示，其中x是一个向量。L2范数可用于衡量向量的大小或长度。

L2范数在机器学习和数据科学中经常用于正则化和优化问题中，例如岭回归和支持向量机等算法。在这些情况下，通过对损失函数添加L2正则化项，可以避免过拟合并提高模型的泛化能力。同时，L2范数也被用来作为相似性度量的度量标准，如余弦相似性。

L2范数公式：
$||x|{|}_2=\sqrt{(\sum |x_i{|}^2)}$

代码实现 ：

import numpy as np 
import matplotlib.pyplot as plt 

模拟数据

X = np.linspace(0, 10, num=30).reshape(-1, 1)
# 斜率和截距，随机生成
w = np.random.randint(1, 5, size=1)
b = np.random.randint(1, 10, size=1)
# 根据一元一次方程计算目标值y并加上‘噪声’，数据有上下波动
y = X * w + b +np.random.randn(30,1)  # 注意要添加噪声避免出现过拟合
plt.scatter(X,y)  # 将图形展现出来

计算斜率和截距

from sklearn.linear_model import LinearRegression
# 创建对象 
model = LinearRegression(fit_intercept=True) # fit_intercept ：是否计算裁距
model.fit(X,y)
print("算法求得的系数,斜率",model.coef_)
print('算法求得的截距',model.intercept_)

和算法求得的斜率和截距进行对比验证

print("这是真实的斜率和截距是",w,b)

获取拟合后的图形

plt.scatter(X,y,color='red')
plt.plot(X,model.coef_*X +model.intercept_,color='green')

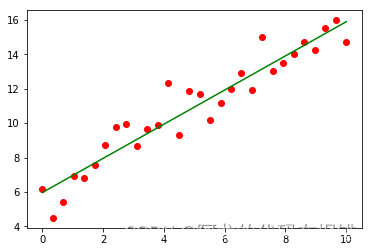
这个时候我们要哦特别注意的是：
model = LinearRegression(fit_intercept=False) # fit_intercept
在使用 LinearRegression创建对象的时候，fit_intercept参数开启则计算裁距
如果不计算裁距情况，如何获得集合的图形

from sklearn.linear_model import LinearRegression
# 创建对象 
model = LinearRegression(fit_intercept=False) # fit_intercept ：是否计算裁距
X_ = np.concatenate([X,np.full(shape=(30,1),fill_value=1)],axis=1)
model.fit(X_,y)
print("算法求得的系数,斜率",model.coef_)
print('算法求得的截距',model.intercept_)

plt.scatter(X,y,color='red')
plt.plot(X,model.coef_[0,0]* X +model.coef_[0,1],color='green')

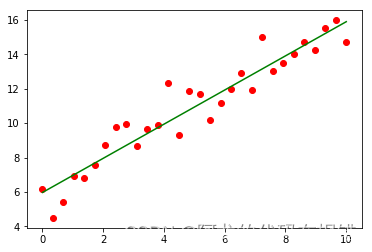
获取系数

np.linalg.inv(X_.T.dot(X_)).dot(X_.T).dot(y)

scikit-learn实现多元的线性回归

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D  # 绘制三维图像

模拟数据

# 转化为矩阵
x1 = np.random.randint(-150, 150, size=(300, 1))
x2 = np.random.randint(0, 300, size=(300, 1))
# 斜率和截距，都是随机生成的
w = np.random.randint(1, 5, size=2)
b = np.random.randint(1, 10, size=1)
# 根据二元一次方程计算目标值y 并且加上“噪声”，让数据上下波动
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300, 1)

创建对象

from sklearn.linear_model import LinearRegression
model = LinearRegression()
X = np.concatenate([x1,x2],axis = 1)
model.fit(X,y)
print(model.coef_,model.intercept_)

输出真实的斜率和系数用于与算法得出的数值进行对比

print(w,b)

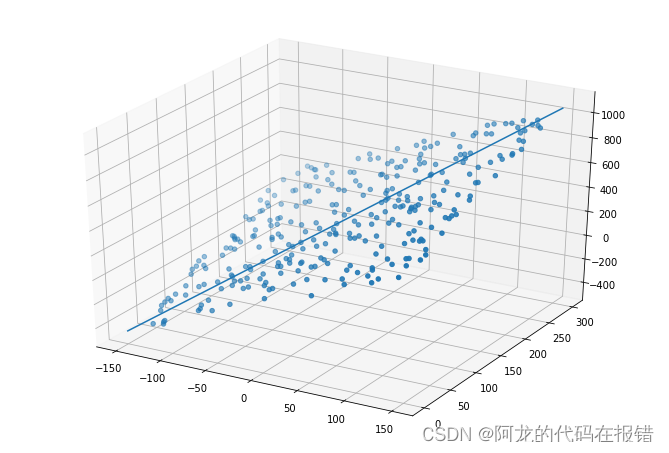
生成拟合图形

# 特征1：x1
x_axis = np.linspace(-150,150,num=500)
# 特征2 ：x2 
y_axis = np.linspace(0,300,num=500)
# 方程 斜率，截距
Z_axis = x_axis * model.coef_[0,0] +y_axis * model.coef_[0,1]+ model.intercept_
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y) #三维散点图
ax.plot(x_axis,y_axis,Z_axis)

坚持学习，整理复盘