回溯算法套路 ①子集型回溯 + 图解 + 笔记

17. 电话号码的字母组合 - 力扣（LeetCode）?

• 17. 电话号码的字母组合 - 力扣（LeetCode）给定一个仅包含数字?2-9?的字符串，返回所有它能表示的字母组合
• 答案可以按?任意顺序?返回
• 给出数字到字母的映射如下（与电话按键相同）
• 注意 1 不对应任何字母

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
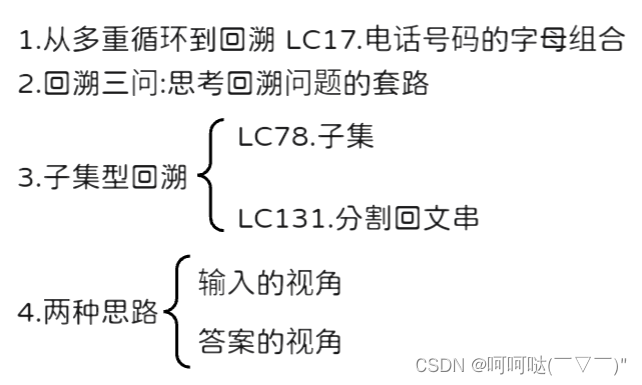
输出：["a","b","c"]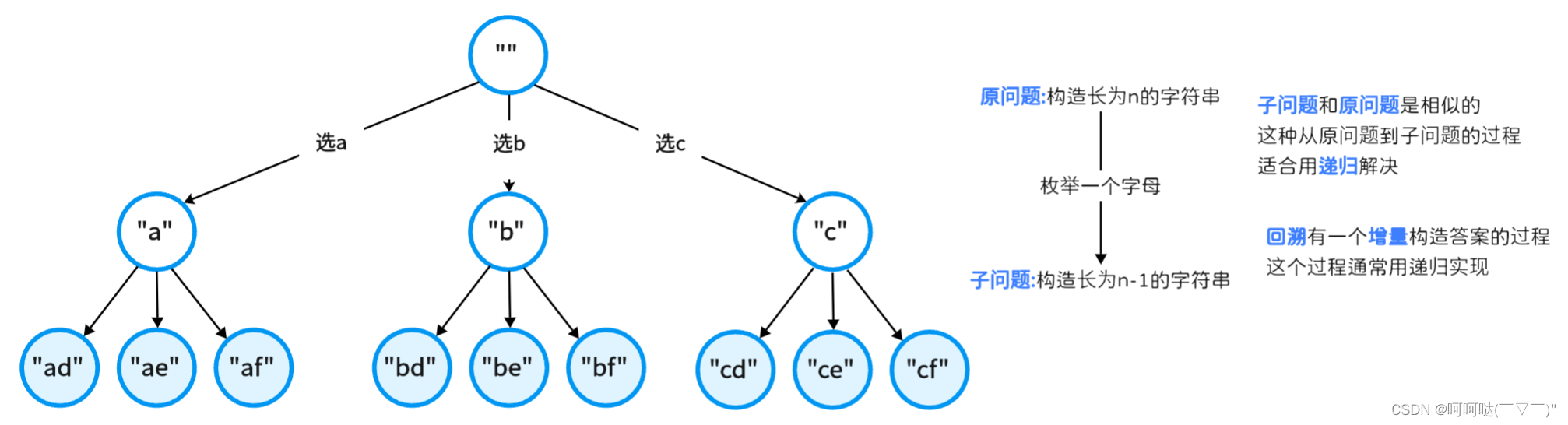

for x in "abc":
    for y in "def":
        ...

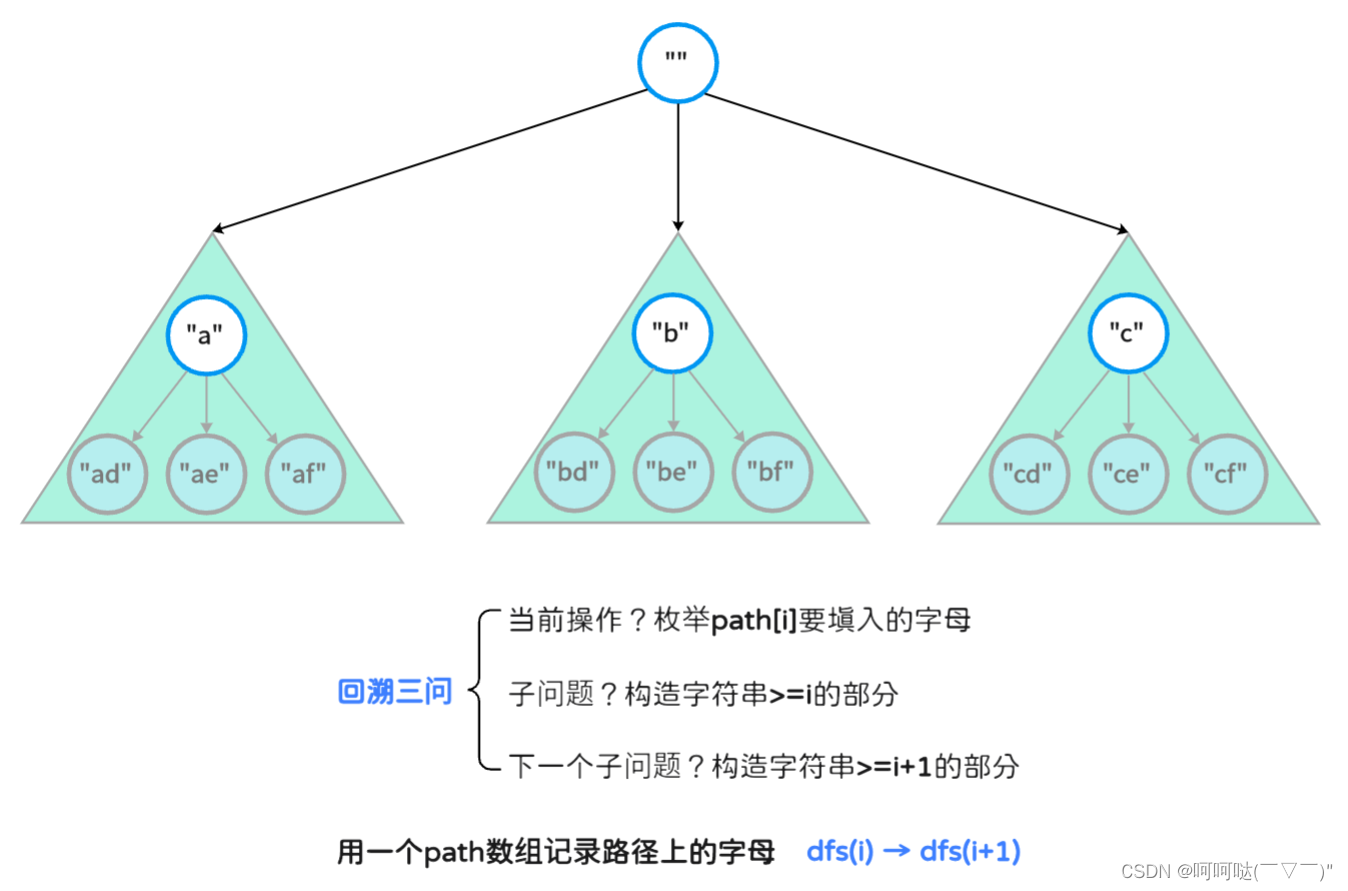
1.构造长为2的字符串，可以写一个二重循环

2.但如果要构造长为3、4的，甚至长度是不确定的，要怎么写呢？

3.单纯的循环嵌套，表达能力是有局限的

C++代码：

class Solution{
    string MAPPING[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
    vector<string> letterCombinations(string digits) {
        int n = digits.length();
        if(n==0) return {};
        vector<string> ans;
        string path;
        function<void(int)> dfs = [&](int i) {
            if(i==n) {
                ans.emplace_back(path);
                return;
            }
            for(char c:MAPPING[digits[i]-'0']) {
                path.push_back(c);
                dfs(i+1);
                path.pop_back();
            }
        };
        dfs(0);
        return ans;
    }
};

class Solution{
    string MAPPING[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
    vector<string> letterCombinations(string digits) {
        int n = digits.length();
        if(n==0) return {};
        vector<string> ans;
        string path(n,0);
        function<void(int)> dfs = [&](int i) {
            if(i==n) {
                ans.emplace_back(path);
                return;
            }
            for(char c:MAPPING[digits[i]-'0']) {
                path[i] = c;
                dfs(i+1);
            }
        };
        dfs(0);
        return ans;
    }
};

• 时间复杂度：
• 空间复杂度：

Python代码:

# Java/C++/Go 等语言的实现，见视频简介
MAPPING = ["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"]
class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        n = len(digits)
        if n==0:
            return []

        # O(n*4^n)
        ans = []
        path = ['']*n
        def dfs(i):
            if i==n:
                ans.append(''.join(path))
                return
            for c in MAPPING[int(digits[i])]:
                path[i]=c
                dfs(i+1)

        dfs(0)
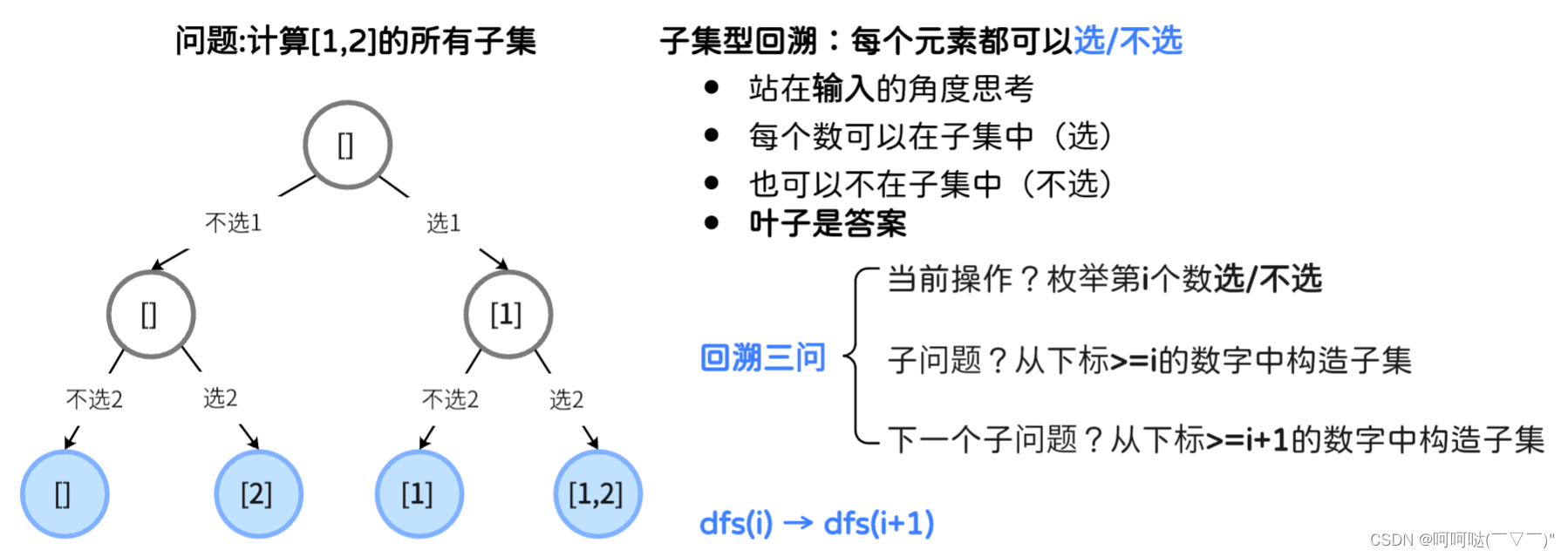
        return ans

78. 子集 - 力扣（LeetCode）?

• 给你一个整数数组?nums?，数组中的元素?互不相同?。返回该数组所有可能的子集（幂集）
• 解集?不能?包含重复的子集。你可以按?任意顺序?返回解集

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

?1.输入的视角（选或不选）

class Solution {
public:
    vector<vector<int>> subsets(vector<int> &nums) {
        vector<vector<int>> ans;
        vector<int> path;
        int n = nums.size();
        function<void(int)> dfs = [&](int i) {
            if(i == n) {
                ans.emplace_back(path);
                return;
            }
            // 不选 nums[i]
            dfs(i+1);
            // 选 nums[i]
            path.push_back(nums[i]);
            dfs(i+1);
            path.pop_back();// 恢复现场
        };
        dfs(0);
        return ans;
    }
};

• ?时间复杂度：
• ?空间复杂度：

?2.答案的视角（选哪个数）?

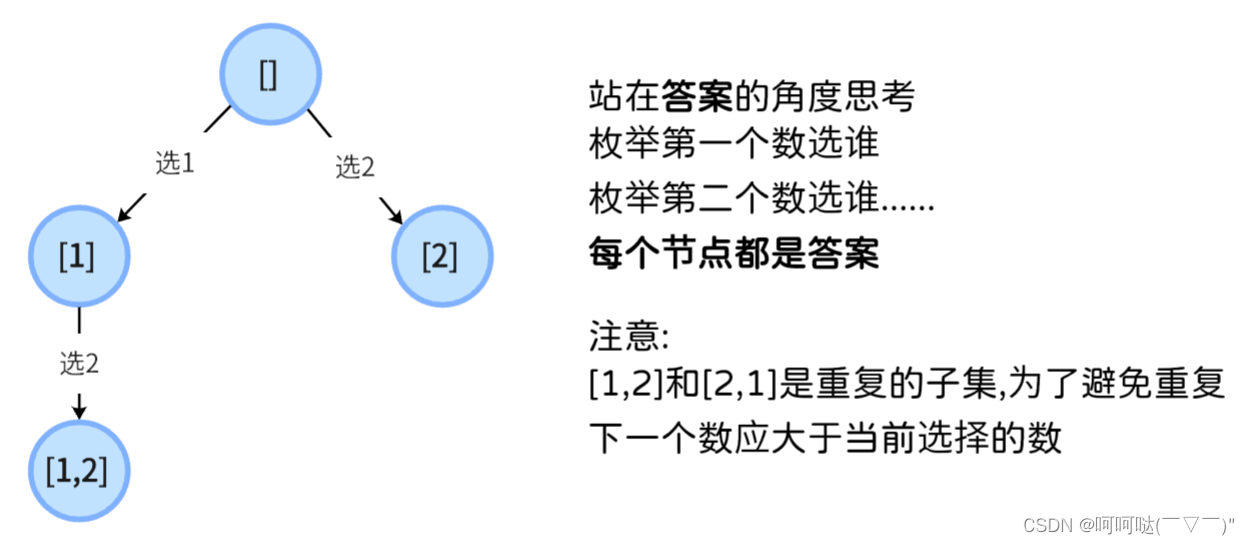
class Solution {
public:
    vector<vector<int>> subsets(vector<int> &nums) {
        vector<vector<int>> ans;
        vector<int> path;
        int n = nums.size();
        function<void(int)> dfs = [&](int i) {
            ans.emplace_back(path);
            if(i == n) {
                return;
            }
            for(int j=i;j<n;j++) { // 枚举选择的数字
                path.push_back(nums[j]);
                dfs(j+1);
                path.pop_back();// 恢复现场
            }
        };
        dfs(0);
        return ans;
    }
};

• ?时间复杂度：
• ?空间复杂度：

131. 分割回文串 - 力扣（LeetCode）

给你一个字符串?s，请你将?s?分割成一些子串，使每个子串都是?回文串?。返回?s?所有可能的分割方案。回文串?是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]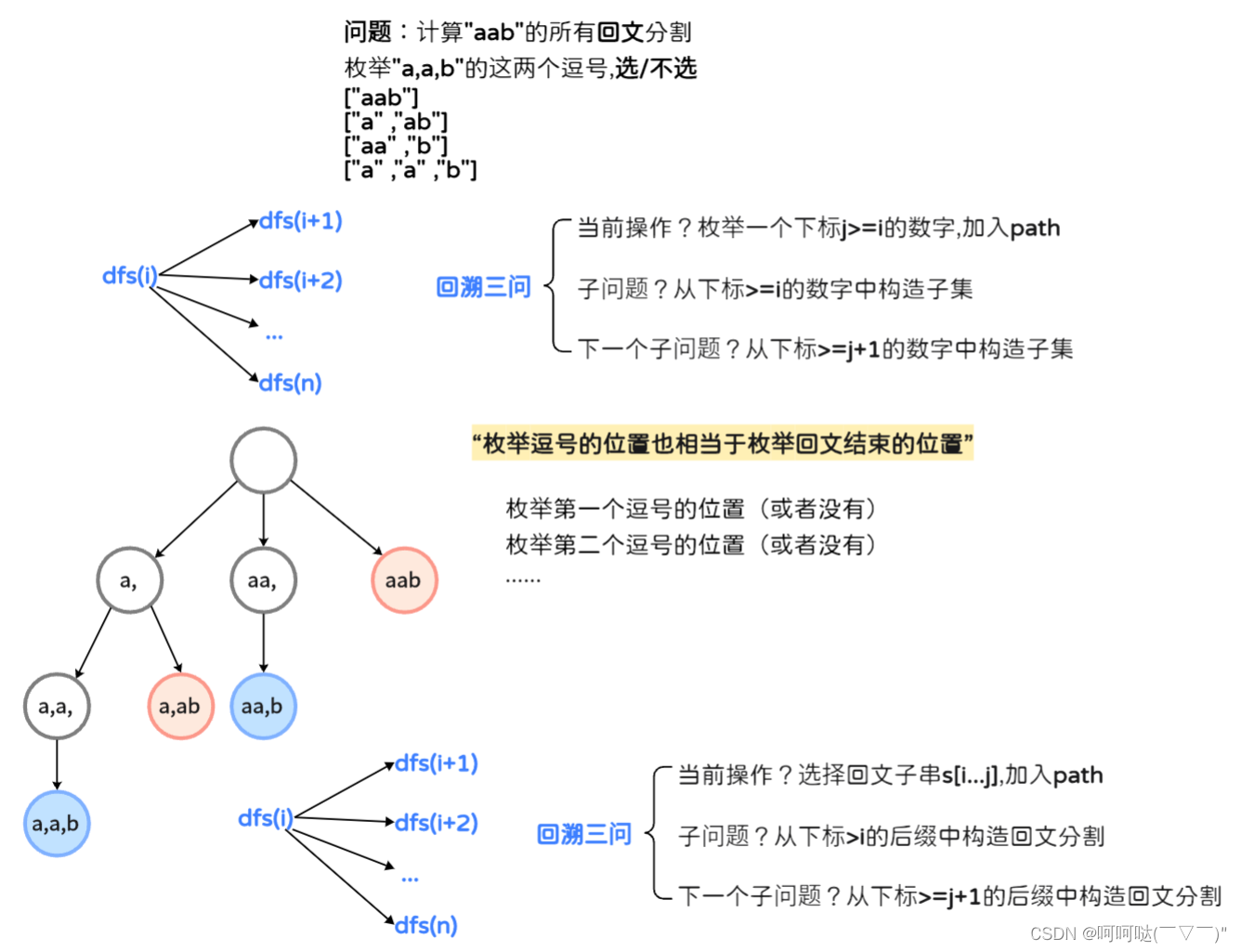

• 方法一：输入的视角（逗号选或不选）

C++代码：

class Solution {
public:
     bool isPalindrome(string &s, int left, int right) {
        while (left < right)
            if (s[left++] != s[right--])
                return false;
        return true;
    }
    /*
        方法一：输入的视角（逗号选或不选）
        假设每对相邻字符之间有个逗号，那么就看每个逗号是选还是不选
        也可以理解成：是否要把s[i]当成分割出的子串的最后一个字符
    */
    vector<vector<string>> partition(string s) {
        vector<vector<string>> ans;
        vector<string> path; // 放已经回文的子串
        int n = s.length();

        // start 表示当前这段回文子串的开始位置
        function<void(int,int)> dfs = [&](int i,int start) {
            if(i == n) {
                ans.emplace_back(path);
                return;
            }

            // 不选 i 和 i+1 之间的逗号（i = n-1 时一定要选）
            if(i < n-1) dfs(i+1,start);

            // 选 i 和 i+1 之间的逗号（把 s[i] 作为子串的最后一个字符）
            if(isPalindrome(s,start,i)) {
                path.push_back(s.substr(start,i-start+1));
                dfs(i+1,i+1);// 下一个子串从 i+1 开始
                path.pop_back();// 恢复现场
            }
        };
        dfs(0,0);
        return ans;
    }
};

• 方法二：答案的视角（枚举子串结束位置）

C++代码：

// 方法二：答案的视角（枚举子串结束位置）
class Solution {
    bool isPalindrome(string &s,int left,int right) {
        while(left < right) {
            if(s[left++] != s[right--]) return false;
        }
        return true;
    }
public:
    vector<vector<string>> partition(string s) {
        vector<vector<string>> ans;
        vector<string> path;
        int n = s.length();
        function<void(int)> dfs = [&](int i) {
            if(i==n) {
                ans.emplace_back(path);
                return;
            }
            for(int j=i;j<n;j++) { // 枚举子串的结束位置
               if(isPalindrome(s,i,j)) {
                    path.push_back(s.substr(i,j-i+1));
                    dfs(j+1);
                    path.pop_back();//恢复现场
               }
            }
        };
        dfs(0);
        return ans;
    }
};

• ?时间复杂度：
• ?空间复杂度：

参考文章和推荐视频：

回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1mG4y1A7Gu/?spm_id_from=333.788&vd_source=a934d7fc6f47698a29dac90a922ba5a3
电话号码的字母组合https://leetcode.cn/problems/letter-combinations-of-a-phone-number/solutions/2059416/hui-su-bu-hui-xie-tao-lu-zai-ci-pythonja-3orv/

78.子集https://leetcode.cn/problems/subsets/solutions/2059409/hui-su-bu-hui-xie-tao-lu-zai-ci-pythonja-8tkl/

131.分割回文串https://leetcode.cn/problems/palindrome-partitioning/solutions/2059414/hui-su-bu-hui-xie-tao-lu-zai-ci-pythonja-fues/?