数模学习day03-层次分析法代码
2023-12-28 18:43:52
这篇文章也是来到了第一讲层次分析法的最后一节，准备浅浅的撒花花吧~~~
进入正题
1.判断矩阵计算权重
计算判断矩阵的时候，要先填好这个矩阵是吧，但是要求是让专家填，但是由于咱学生一般是请不到专家来的，所以说就咱自己填就可以了，也别说是谁填的了。
填完之后，记住要进行一致性检验，通过之后使用第一篇文章介绍了三种方法计算权重。
一致性检验的步骤
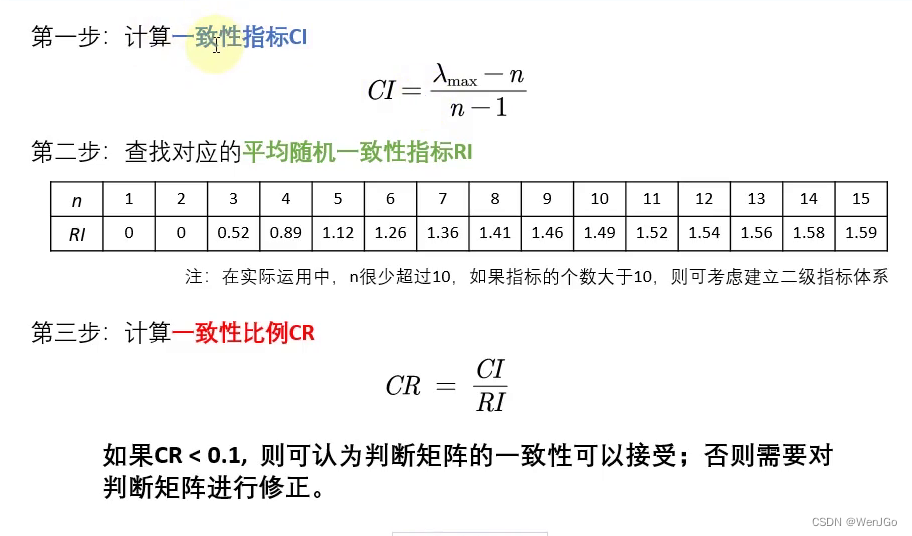
但是由于一致性检验的时候需要使用特征值，所以你可以先把特征值求权重算出来，再一致性检验啥的，比较快。
2.代码实现
注意
????????注意：在论文写作中，应该先对判断矩阵进行一致性检验，然后再计算权重，因为只有判断矩阵通过了一致性检验，其权重才是有意义的。
????????在下面的代码中，我们先计算了权重，然后再进行了一致性检验，这是为了顺应计算过程，事实上在逻辑上是说不过去的。
????????因此大家自己写论文中如果用到了层次分析法，一定要先对判断矩阵进行一致性检验。
????????要说明的是，只有非一致矩阵的判断矩阵才需要进行一致性检验。
????????如果你的判断矩阵本身就是一个一致矩阵，那么就没有必要进行一致性检验。
代码
（1）首先先输入判断矩阵
记住，判断矩阵里面的元素只能是1·9，或者它们的倒数
clear;clc
disp('请输入判断矩阵A： ')
% A = input('判断矩阵A=')? 使用这一行代码是一样的效果
A =[1 1 4 1/3 3;
?1 1 4 1/3 3;
?1/4 1/4 1 1/3 1/2;
?3 3 3 1 3;
?1/3 1/3 2 1/3 1]
% matlab矩阵有两种写法，也可以直接写到一行:
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 也可以写成多行:
% [1 1 4 1/3 3;
% ?1 1 4 1/3 3;
% ?1/4 1/4 1 1/3 1/2;
% ?3 3 3 1 3;
% ?1/3 1/3 2 1/3 1]
% 两行之间以分号结尾（最后一行的分号可加可不加），同行元素之间以空格（或者逗号）分开。（2）使用算术平均法求权重
% 第一步：将判断矩阵按照列归一化（每一个元素除以其所在列的和）
% 所以在这里先计算一下所在列的和
Sum_A = sum(A)
% 也可以写成n = size(A,1)
% 因为这里A判断矩阵是一个方阵，所以行列数量相同，就都使用n了
[n,n] = size(A)
% 将这个Sum_A也重复为方阵,以达到后面的每一个元素 点除 达到第一步的目的
SUM_A = repmat(Sum_A,n,1)
% 另外一种替代的方法（循环）如下：
SUM_A = [];
for i = 1:n %循环哦，这一行后面不能加冒号（和Python不同），这里表示循环n次
% 这个操作就是往SUM_A中每次加一行Sum_A五次之后就是五行了
SUM_A = [SUM_A; Sum_A]
end
clc;A
SUM_A
% 这里我们直接将两个矩阵对应的元素相除即可
Stand_A = A ./ SUM_A
% 第二步：将归一化的各列相加(按行求和)
sum(Stand_A,2)
% 第三步：将相加后得到的向量中每个元素除以n即可得到权重向量
disp('算术平均法求权重的结果为：');
% 首先对标准化后的矩阵按照行求和，得到一个列向量
% 然后再将这个列向量的每个元素同时除以n即可（注意这里也可以用 / 因为只有一列，所以效果是一样的）
disp(sum(Stand_A,2) ./ n)
结果如下：
>> disp(sum(Stand_A,2) ./ n)
? ? 0.2145
? ? 0.2145
? ? 0.0703
? ? 0.4006
? ? 0.1001
?
（3）使用几何平均法求权重
代码示例：
% 第一步：将A的元素按照行相乘得到一个新的列向量
clc;A
% prod函数和sum函数类似，一个用于乘，一个用于加 dim = 2 维度是行
% prod也就是把每一行的元素乘去来起来
Prduct_A = prod(A,2)
% 第二步：将新的向量的每个分量开n次方
% 这里对每个元素进行乘方操作，因此要加.号。 ^符号表示乘方 这里是开n次方，所以我们等价求1/n次方
Prduct_n_A = Prduct_A .^ (1/n)
% 第三步：对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个 向量的和 即可
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))
答案如下：?
几何平均法求权重的结果为：
? ? 0.2184
? ? 0.2184
? ? 0.0664
? ? 0.3985
? ? 0.0983
（4）特征值法求权重
代码示例：?
% 第一步：求出矩阵A的最大特征值以及其对应的特征向量
clc
%V是特征向量, D是由特征值构成的对角矩阵（除了对角线元素外，其余位置元素全为0）
[V,D] = eig(A)
%也可以写成max(D(:))
% 这里max函数就可以找到最大的特征值，即使有虚数也无所谓，他可以根据模长找
% max找的是每一列的最大，因此使用两次就可以知道矩阵中的最大值是多少了
Max_eig = max(max(D))
% 那么怎么找到最大特征值所在的位置？ 这里就需要使用到find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 那么问题来了，我们要得到最大特征值的位置，就需要将包含所有特征值的这个对角矩阵D中，不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置，记录它的行和列。
% 第二步：对求出的特征向量进行归一化即可得到我们的权重
% V(:,c) 取出对应的特征向量
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量，然后再进行标准化。
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )
答案为：
特征值法求权重的结果为：
? ? 0.2121
? ? 0.2121
? ? 0.0679
? ? 0.4114
? ? 0.0965
（5）一致性检验
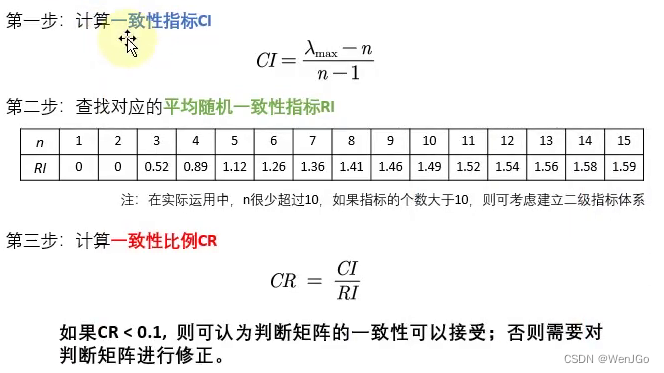
代码示例：
clc
CI = (Max_eig - n) / (n-1);
% 注意，这里的RI最多支持 n = 15
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
% disp(['一致性指标CI=', num2str(CI)]);这样写和下面是一个样子的
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR < 0.10，所以该判断矩阵A的一致性可以接受!');
else
disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end结果如下：
一致性指标CI=
? ? 0.0731一致性比例CR=
? ? 0.0653因为CR < 0.10，所以该判断矩阵A的一致性可以接受!
3.隐藏BUG
1.如果这个输入的矩阵是一个二阶的判断阵，会有什么问题？如何改正？
如果这个矩阵是一个 A = [1,1 ; 1,1]的矩阵会发生什么
这时候你再计算一致性比例会发生什么呢？
为什么呢？
因为这里的最大特征值是
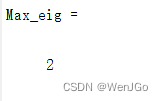
然后n也是
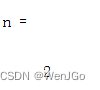
RI在n取2的时候是0
那么最后就是 0/0得到
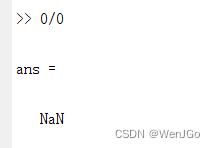
因为这里的判断阵是一个正互反矩阵，然后又只是二阶的，所以它一定是一个一致性矩阵，这里就不需要进行一致性检验了。
但是为了防止报错也可以通过将RI的第二个零设置为0.001
2.如何判断你输入的是否有错误
disp('请输入判断矩阵A');
A=input('A=');
% 这里输入的就是我们的判断矩阵，其为n阶方阵（行数和列数相同）
% [1 3 1/3 1/3 1 1/3;1/3 1 1/4 1/5 1 1/5;3 4 1 1 2 3;3 5 1 1 2 1;1 1 1/2 1/2 1 1;3 5 1/3 1 1 1]
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 在开始下面正式的步骤之前，我们有必要检验下A是否因为粗心而输入有误
ERROR = 0; % 默认输入是没有错误的
%(1)检查矩阵A的维数是否不大于1或不是方阵
[r,c]=size(A);
% 注意!!1不等号是 ~= (~是键盘Tab上面那个键，要和Shift键同时按才会出来)，别和java等语言里面的!=搞混了
% ||表示逻辑运算符‘或’ 逻辑运算符且是 && （&读and，连接符号，是and的缩写。 ）这里和其他编程语言是一样的
% Matlab的判断语句，if所在的行不需要冒号，语句的最后一定要以end结尾 ；中间的语句要注意缩进。
if r ~= c || r <= 1
ERROR = 1;
end
%(2)检验是否为正互反矩阵 a_ij > 0 且 a_ij * a_ji = 1
if ERROR == 0
[n,n] = size(A);
% 因为我们的判断矩阵A是一个非零方阵，所以这里的r和c相同，我们可以就用同一个字母n表示
% 判断是否有元素小于0
% for i = 1:n
% for j = 1:n
% if A(i,j)<=0
% ERROR = 2;
% end
% end
% end
if sum(sum(A <= 0)) > 0
ERROR = 2;
end
end
% 检验n是否超过了15，因为RI向量为15维
if ERROR == 0
if n > 15
ERROR = 3;
end
end
if ERROR == 0
% 判断 a_ij * a_ji = 1 是否成立
if sum(sum(A' .* A ~= ones(n))) > 0
ERROR = 4;
end
% A' 表示求出 A 的转置矩阵，即将a_ij和a_ji互换位置,'是一个单引号
% ones(n)函数生成一个n*n的全为1的方阵, zeros(n)函数生成一个n*n的全为0的方阵
% ones(m,n)函数生成一个m*n的全为1的矩阵
% MATLAB在矩阵的运算中，“/”号和“*”号代表矩阵之间的乘法与除法，对应元素之间的乘除法需要使用“./”和“.*”
% 如果a_ij * a_ji = 1 满足， 那么A和A'对应元素相乘应该为1
end
if ERROR == 0
% % % % % % % % % % % % %方法1： 算术平均法求权重% % % % % % % % % % % % %
% 第一步：将判断矩阵按照列归一化（每一个元素除以其所在列的和）
% 第二步：将归一化的各列相加
% 第三步：将相加后的向量除以n即可得到权重向量
Sum_A = sum(A);
% matlab中的sum函数的用法
% a=sum(x);%按列求和
% a=sum(x,2);%按行求和
% a=sum(x(:));%对整个矩阵求和
% % 基础：matlab中如何提取矩阵中指定位置的元素？
% % （1）取指定行和列的一个元素（输出的是一个值）
% % A(2,1) A(3,2)
% % （2）取指定的某一行的全部元素（输出的是一个行向量）
% % A(2,:) A(5,:)
% % （3）取指定的某一列的全部元素（输出的是一个列向量）
% % A(:,1) A(:,3)
% % （4）取指定的某些行的全部元素（输出的是一个矩阵）
% % A([2,5],:) 只取第二行和第五行（一共2行）
% % A(2:5,:) 取第二行到第五行（一共4行）
% % （5）取全部元素(按列拼接的，最终输出的是一个列向量)
% % A(:)
SUM_A = repmat(Sum_A,n,1);
% B = repmat(A,m,n):将矩阵A复制m×n块，即把A作为B的元素，B由m×n个A平铺而成。
% 另外一种替代的方法如下：
% SUM_A = [];
% for i = 1:n %循环哦，不需要加冒号，这里表示循环n次
% SUM_A = [SUM_A;Sum_A];
% end
Stand_A = A ./ SUM_A;
% MATLAB在矩阵的运算中，“*”号和“/”号代表矩阵之间的乘法与除法，对应元素之间的乘除法需要使用“./”和“.*”
% 这里我们直接将两个矩阵对应的元素相除即可
disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2) / n)
% 首先对标准化后的矩阵按照行求和，得到一个列向量，然后再将这个列向量的每个元素同时除以n即可（注意这里也可以用./哦）
% % % % % % % % % % % % %方法2： 几何平均法求权重% % % % % % % % % % % % %
% 第一步：将A的元素按照行相乘得到一个新的列向量
Prduct_A = prod(A,2);
% prod函数和sum函数类似，一个用于乘，一个用于加
% 第二步：将新的向量的每个分量开n次方
Prduct_n_A = Prduct_A .^ (1/n);
% 这里对元素操作，因此要加.号哦。 ^符号表示乘方哦 这里是开n次方，所以我们等价求1/n次方
% 第三步：对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))
% % % % % % % % % % % % %方法3： 特征值法求权重% % % % % % % % % % % % %
% 计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法：
% （1）E=eig(A)：求矩阵A的全部特征值，构成向量E。
% （2）[V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。（V的每一列都是D中与之相同列的特征值的特征向量）
[V,D] = eig(A); %V是特征向量, D是由特征值构成的对角矩阵（除了对角线元素外，其余位置元素全为0）
Max_eig = max(max(D)); %也可以写成max(D(:))哦~
% 那么怎么找到最大特征值所在的位置了？ 需要用到find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 下面例子来自博客：https://www.cnblogs.com/anzhiwu815/p/5907033.html
% 关于find函数的更加深入的用法可参考原文
% >> X = [1 0 4 -3 0 0 0 8 6];
% >> ind = find(X)
% ind =
% 1 3 4 8 9
% 其有多种用法，比如返回前2个不为0的元素的位置：
% >> ind = find(X,2)
% >> ind =
% 1 3
%若X是一个矩阵，索引该如何返回呢？
% >> X = [1 -3 0;0 0 8;4 0 6]
% X =
% 1 -3 0
% 0 0 8
% 4 0 6
% >> ind = find(X)
% ind =
% 1
% 3
% 4
% 8
% 9
% 这是因为在Matlab在存储矩阵时，是一列一列存储的，我们可以做一下验证：
% >> X(4)
% ans =
% -3
% 假如你需要按照行列的信息输出该怎么办呢？
% [r,c] = find(X)
% r =
% 1
% 3
% 1
% 2
% 3
% c =
% 1
% 1
% 2
% 3
% 3
% [r,c] = find(X,1) %只找第一个非0元素
% r =
% 1
% c =
% 1
% 那么问题来了，我们要得到最大特征值的位置，就需要将包含所有特征值的这个对角矩阵D中，不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算，共有三种运算符：大于> ;小于< ;等于 == （一个等号表示赋值；两个等号表示判断）
% 例如：A > 2 会生成一个和A相同大小的矩阵，矩阵元素要么为0，要么为1（A中每个元素和2比较，如果大于2则为1，否则为0）
[r,c]=find(D == Max_eig , 1);
% 找到D中第一个与最大特征值相等的元素的位置，记录它的行和列。
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量，然后再进行标准化。
% % % % % % % % % % % % %下面是计算一致性比例CR的环节% % % % % % % % % % % % %
% 当CR<0.10时，我们认为判断矩阵的一致性可以接受；否则应对其进行修正。
CI = (Max_eig - n) / (n-1);
RI=[0 0.00001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦，这里的RI最多支持 n = 15
% 这里n=2时，一定是一致矩阵，所以CI = 0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
else
disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end
elseif ERROR == 1
disp('请检查矩阵A的维数是否不大于1或不是方阵')
elseif ERROR == 2
disp('请检查矩阵A中有元素小于等于0')
elseif ERROR == 3
disp('A的维数n超过了15，请减少准则层的数量')
elseif ERROR == 4
disp('请检查矩阵A中存在i、j不满足A_ij * A_ji = 1')
end该代码起到了一个交互的作用，用于检验A是否满足规定
总结
没有总结，赶进度呢，ヾ(￣▽￣)Bye~Bye~
文章来源:https://blog.csdn.net/DDDDWJDDDD/article/details/135266931
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！