LeetCode-周赛-思维训练-中等难度

第一题

1798. 你能构造出连续值的最大数目

解题思路

我们先抛开原题不看，可以先完成一道简单的题目，假设现在就给你一个目标值X，问你能够构造出从【1~X】的连续整数，最小需要几个数？

贪心假设

期望：我们要尽量用最少的数目，构造出最长的连续数字。

使用数组` x = [1]`，那么能构造出来的连续整数的范围就是`【1】` 
使用数组 `x = [1,2]`，那么能构造出来的连续整数的范围就是`【1~3】` 
使用数组 `x = [1,2,4]`，那么能构造出来的连续整数的范围就是`【1~7】` 
	使用数组`x = [1,2,3]`，那么只能构造出`【1~6】`。
	而同样是`3`个数，`x = [1,2,4]`，却能构造出`【1~7】`。
	所以在尽量少的数目前提下，选择：`[1,2,4]` 
使用数组 `x = [1,2,4,8]`，那么能构造出来的连续整数的范围就是`【1~15】`

结论：如果有一些已经从小到大排序好的数`【a1,a2,a3...an】`，能够连续构造出来的整数范围是`【1~N】`，那么下一个能够造成的最大范围则为`【1~ (N + N +1)】`

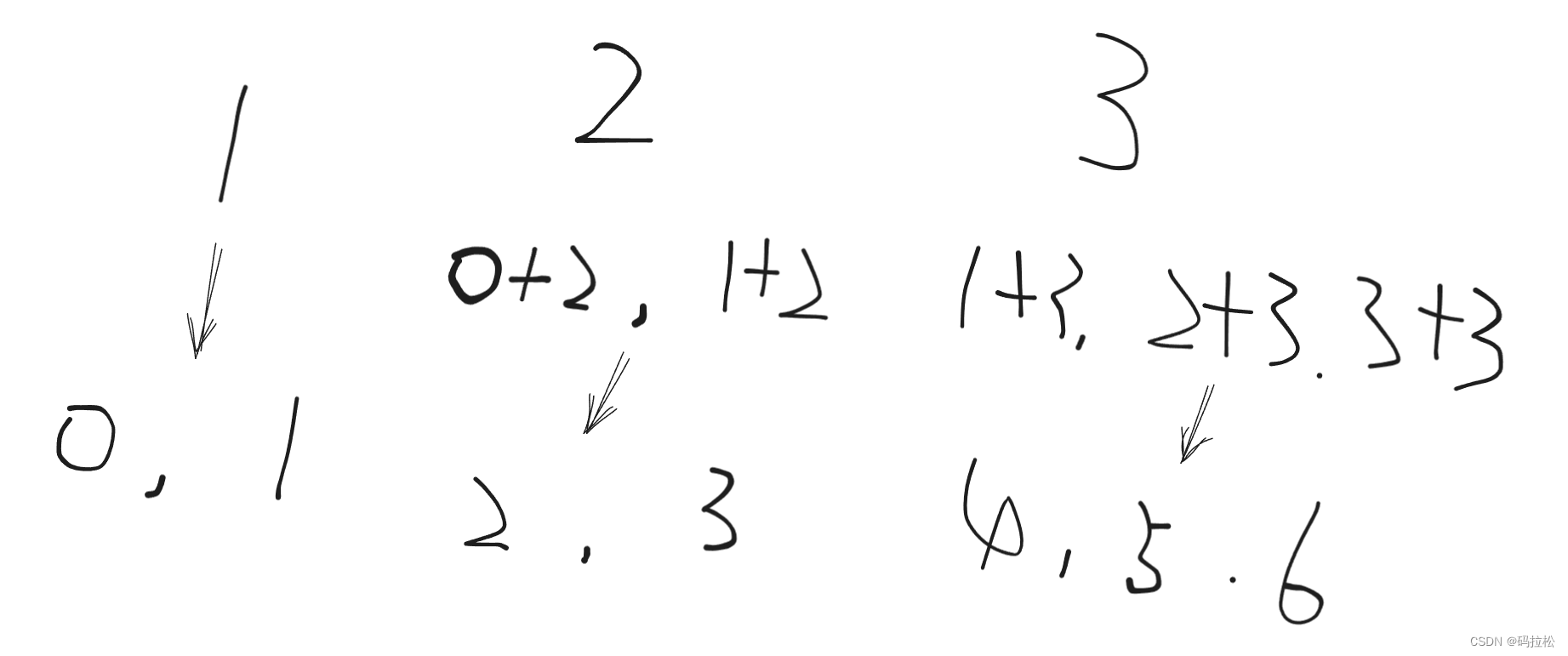
根据结论，我们很容易给出代码实现

public int simple_minimumAdded(int target) {
    int ans = 0;
    int n = 0;
    while (n < target) {
      n = n + n + 1;
      ans++;
    }
    return ans;
}

现在，让我们回到原题中，虽然题目中给出的coins数组所包含的元素并不是按照最佳期望给的，但这并不影响整体的解题方式。

比如，题目中的示例2：`coins = [1,1,1,4]`，我们还是将数组分解拆开讨论

当 `coins = [1]` 时，范围 `【1】`
当 `coins = [1,1]` 时，范围 `【1~2】`
当 `coins = [1,1,1] `时，范围 `【1~3】`
当 `coins = [1,1,1,4] `时，范围 `【1~7】`

结论：如果有一些已经从小到大排序好的数`【a1,a2,a3...an】`，能够连续构造出来的整数范围是`【1~N】`，那么下一个能够造成的最大范围则为`【1 ~ (an + N)】`。

但是这里还有一个前提，`an`如果大于`N+1`，则就无法构造连续整数了，且缺失的连续整数为`【N + 1 ~ an - 1】`

把4换成6，连续范围只能是【1~3】和【6~9】缺4和5两个数字。

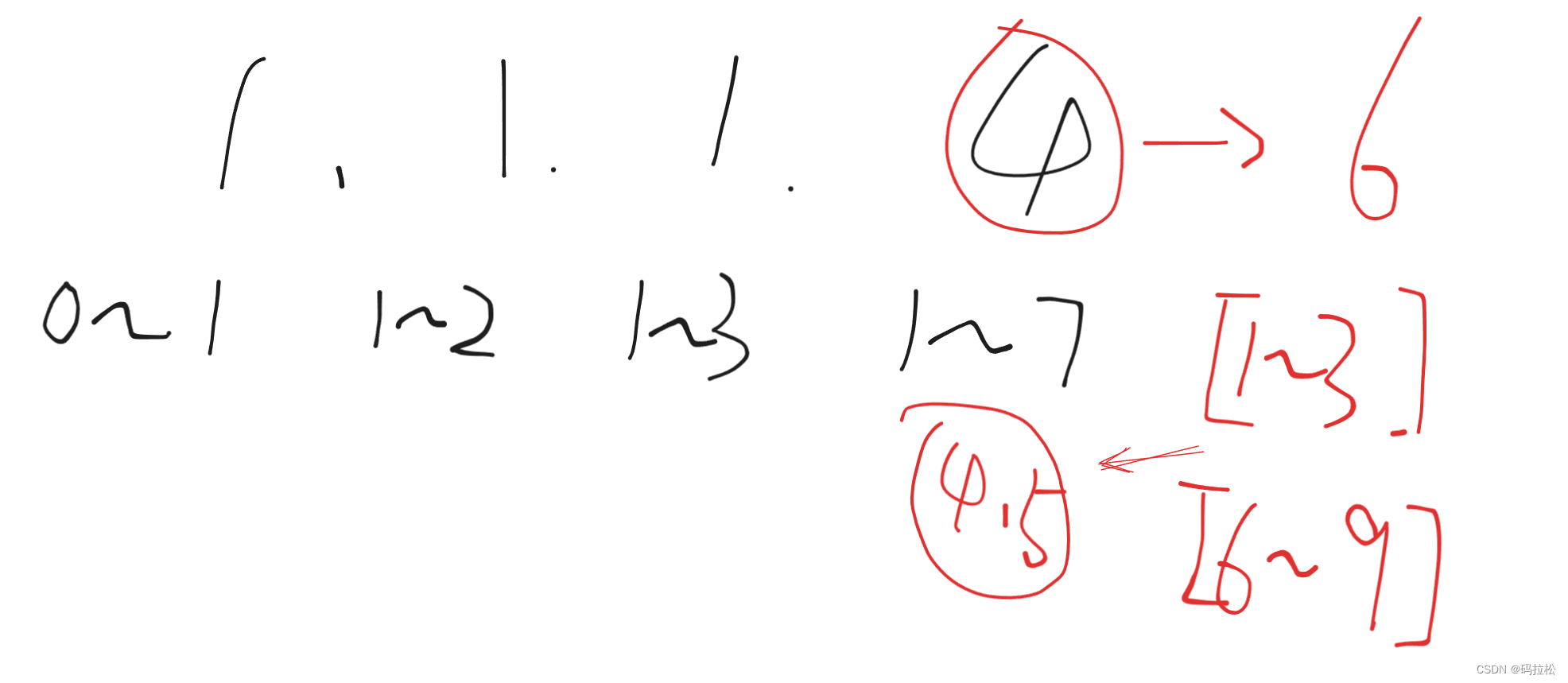
代码实现

根据这个结论，本题的代码实现如下：

class Solution {
    public int getMaximumConsecutive(int[] coins) {
        Arrays.sort(coins);
        int n = 0;
        for(int c : coins){
            if(c > n + 1){
                break;
            }
            n += c;
        }
        // 由于题目中0也算一个数，所以最后答案为: n + 1
        return n + 1;
    }
}

第二题

2952. 需要添加的硬币的最小数量

在有了前一题的基础上，再来做这一题，就简单了许多，本题可以看作当数组无法构造连续整数，且又未达到target时，你可以通过添加一些数字，使其满足要求，问你最少需要添加几次。

代码实现

class Solution {
    public int minimumAddedCoins(int[] coins, int target) {
        Arrays.sort(coins);
        long max = 0;
        int idx = 0;
        int ans = 0;
        while (max < target) {
            if (idx < coins.length && coins[idx] <= max + 1) {
                max += coins[idx];
                idx++;
            } else {
                max = max + max + 1;
                ans++;
            }
        }
        return ans;
    }
}

整个实现逻辑，实际上就是分别考虑了两种情况，一种是数组中的元素本身可以维持连续性，一种是数组中的元素本身无法维持连续性，需要补齐。而面对这两种情况下的处理方式实际上就是前一题中的解法。