Python绘制多分类ROC曲线
2023-12-13 12:29:45
目录
1 数据集介绍
1.1 数据集简介
分类数据集为某公司手机上网满意度数据集,数据如图所示,共7020条样本,关于手机满意度分类的特征有网络覆盖与信号强度、手机上网速度、手机上网稳定性等75个特征。
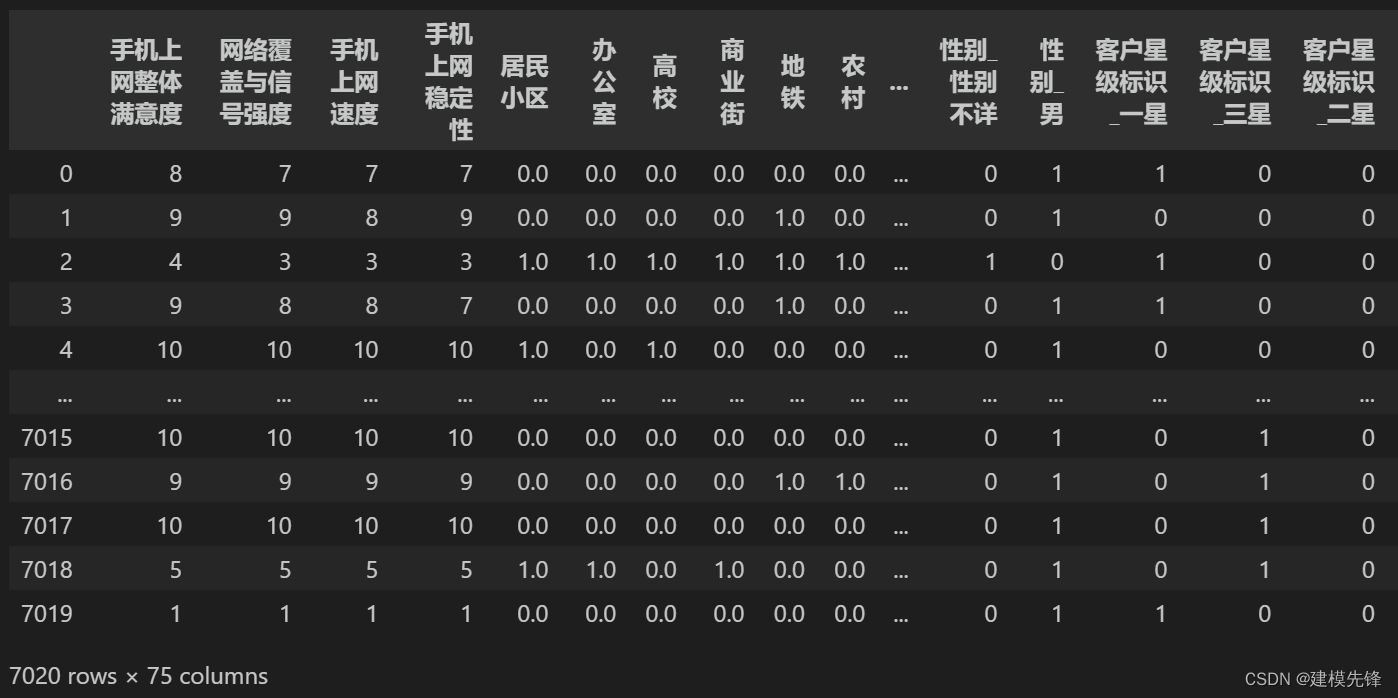
1.2 数据预处理
常规数据处理流程,详细内容见上期随机森林处理流程:
xxx 链接
-
缺失值处理
-
异常值处理
-
数据归一化
-
分类特征编码
处理完后的数据保存为?手机上网满意度.csv文件(放置文末)
?2随机森林分类
2.1 数据加载
第一步,导入包
import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestClassifier# 随机森林回归
from sklearn.model_selection import train_test_split,GridSearchCV,cross_val_score
from sklearn.metrics import accuracy_score # 引入准确度评分函数
from sklearn.metrics import mean_squared_error
from sklearn import preprocessing
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')第二步,加载数据
net_data = pd.read_csv('手机上网满意度.csv')
Y = net_data.iloc[:,3]
X= net_data.iloc[:, 4:]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=200) # 随机数种子
print(net_data.shape)
net_data.describe()
2.2 参数寻优
第一步,对最重要的超参数n_estimators即决策树数量进行调试,通过不同数目的树情况下,在训练集和测试集上的均方根误差来判断
## 分析随着树数目的变化,在测试集和训练集上的预测效果
rfr1 = RandomForestClassifier(random_state=1)
n_estimators = np.arange(50,500,50) # 420,440,2
train_mse = []
test_mse = []
for n in n_estimators:
rfr1.set_params(n_estimators = n) # 设置参数
rfr1.fit(X_train,Y_train) # 训练模型
rfr1_lab = rfr1.predict(X_train)
rfr1_pre = rfr1.predict(X_test)
train_mse.append(mean_squared_error(Y_train,rfr1_lab))
test_mse.append(mean_squared_error(Y_test,rfr1_pre))
## 可视化不同数目的树情况下,在训练集和测试集上的均方根误差
plt.figure(figsize=(12,9))
plt.subplot(2,1,1)
plt.plot(n_estimators,train_mse,'r-o',label='trained MSE',color='darkgreen')
plt.xlabel('Number of trees')
plt.ylabel('MSE')
plt.grid()
plt.legend()
plt.subplot(2,1,2)
plt.plot(n_estimators,test_mse,'r-o',label='test MSE',color='darkgreen')
index = np.argmin(test_mse)
plt.annotate('MSE:'+str(round(test_mse[index],4)),
xy=(n_estimators[index],test_mse[index]),
xytext=(n_estimators[index]+2,test_mse[index]+0.000002),
arrowprops=dict(facecolor='red',shrink=0.02))
plt.xlabel('Number of trees')
plt.ylabel('MSE')
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()
以及最优参数和最高得分进行分析,如下所示
###调n_estimators参数
ScoreAll = []
for i in range(50,500,50):
DT = RandomForestClassifier(n_estimators = i,random_state = 1) #,criterion = 'entropy'
score = cross_val_score(DT,X_train,Y_train,cv=6).mean()
ScoreAll.append([i,score])
ScoreAll = np.array(ScoreAll)
max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] ##这句话看似很长的,其实就是找出最高得分对应的索引
print("最优参数以及最高得分:",ScoreAll[max_score])
plt.figure(figsize=[20,5])
plt.plot(ScoreAll[:,0],ScoreAll[:,1],'r-o',label='最高得分',color='orange')
plt.xlabel('n_estimators参数')
plt.ylabel('分数')
plt.grid()
plt.legend()
plt.show()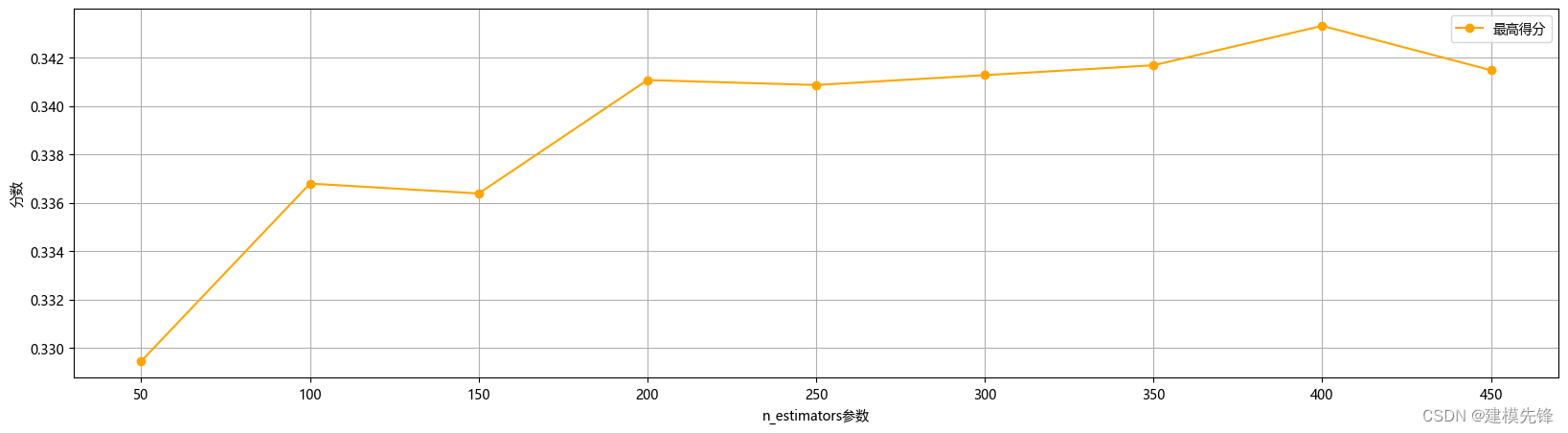 很明显,决策树个数设置在400的时候回归森林预测模型的测试集均方根误差最小,得分最高,效果最显著。因此,我们通过网格搜索进行小范围搜索,构建随机森林预测模型时选取的决策树个数为400。
很明显,决策树个数设置在400的时候回归森林预测模型的测试集均方根误差最小,得分最高,效果最显著。因此,我们通过网格搜索进行小范围搜索,构建随机森林预测模型时选取的决策树个数为400。
第二步,在确定决策树数量大概范围后,搜索决策树的最大深度的最高得分,如下所示
# 探索max_depth的最佳参数
ScoreAll = []
for i in range(4,14,2):
DT = RandomForestClassifier(n_estimators = 400,random_state = 1,max_depth =i ) #,criterion = 'entropy'
score = cross_val_score(DT,X_train,Y_train,cv=6).mean()
ScoreAll.append([i,score])
ScoreAll = np.array(ScoreAll)
max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0]
print("最优参数以及最高得分:",ScoreAll[max_score])
plt.figure(figsize=[20,5])
plt.plot(ScoreAll[:,0],ScoreAll[:,1])
plt.xlabel('max_depth最佳参数')
plt.ylabel('分数')
plt.grid()
plt.legend()
plt.show() 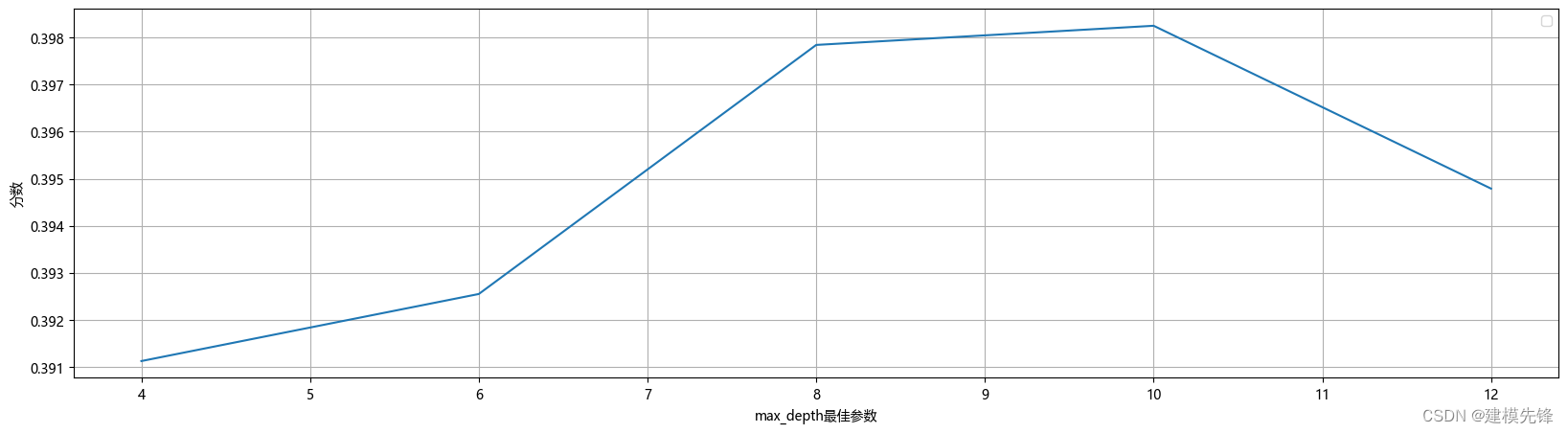
决策树的深度最终设置为10。
2.3 模型训练与评估
# 随机森林 分类模型
model = RandomForestClassifier(n_estimators=400,max_depth=10,random_state=1) # min_samples_leaf=11
# 模型训练
model.fit(X_train, Y_train)
# 模型预测
y_pred = model.predict(X_test)
print('训练集模型分数:', model.score(X_train,Y_train))
print('测试集模型分数:', model.score(X_test,Y_test))
print("训练集准确率: %.3f" % accuracy_score(Y_train, model.predict(X_train)))
print("测试集准确率: %.3f" % accuracy_score(Y_test, y_pred))
绘制混淆矩阵:
# 混淆矩阵
from sklearn.metrics import confusion_matrix
import matplotlib.ticker as ticker
cm = confusion_matrix(Y_test, y_pred,labels=[1,2,3,4,5,6,7,8,9,10]) # ,
print('混淆矩阵:\n', cm)
labels=['1','2','3','4','5','6','7','8','9','10']
from sklearn.metrics import ConfusionMatrixDisplay
cm_display = ConfusionMatrixDisplay(cm,display_labels=labels).plot()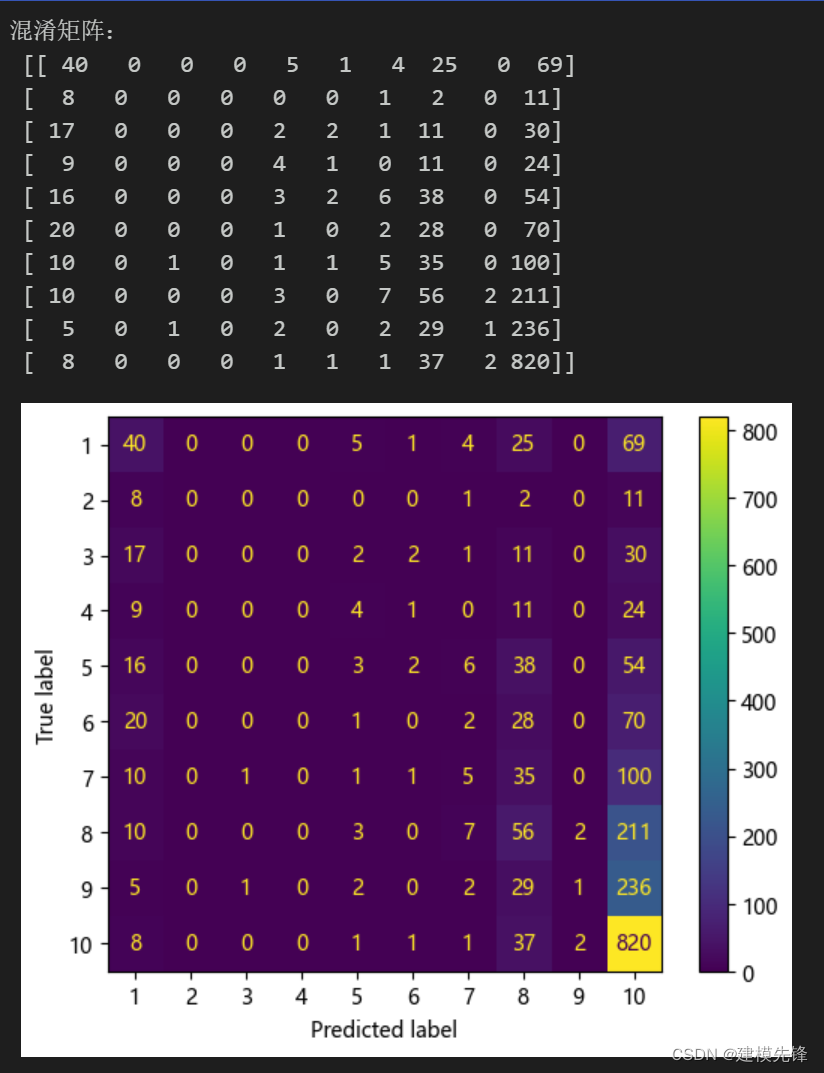
3 绘制十分类ROC曲线
第一步,计算每个分类的预测结果概率
from sklearn.metrics import roc_curve,auc
df = pd.DataFrame()
pre_score = model.predict_proba(X_test)
df['y_test'] = Y_test.to_list()
df['pre_score1'] = pre_score[:,0]
df['pre_score2'] = pre_score[:,1]
df['pre_score3'] = pre_score[:,2]
df['pre_score4'] = pre_score[:,3]
df['pre_score5'] = pre_score[:,4]
df['pre_score6'] = pre_score[:,5]
df['pre_score7'] = pre_score[:,6]
df['pre_score8'] = pre_score[:,7]
df['pre_score9'] = pre_score[:,8]
df['pre_score10'] = pre_score[:,9]
pre1 = df['pre_score1']
pre1 = np.array(pre1)
pre2 = df['pre_score2']
pre2 = np.array(pre2)
pre3 = df['pre_score3']
pre3 = np.array(pre3)
pre4 = df['pre_score4']
pre4 = np.array(pre4)
pre5 = df['pre_score5']
pre5 = np.array(pre5)
pre6 = df['pre_score6']
pre6 = np.array(pre6)
pre7 = df['pre_score7']
pre7 = np.array(pre7)
pre8 = df['pre_score8']
pre8 = np.array(pre8)
pre9 = df['pre_score9']
pre9 = np.array(pre9)
pre10 = df['pre_score10']
pre10 = np.array(pre10)第二步,画图数据准备
y_list = df['y_test'].to_list()
pre_list=[pre1,pre2,pre3,pre4,pre5,pre6,pre7,pre8,pre9,pre10]
lable_names=['1','2','3','4','5','6','7','8','9','10']
colors1 = ["r","b","g",'gold','pink','y','c','m','orange','chocolate']
colors2 = "skyblue"# "mistyrose","skyblue","palegreen"
my_list = []
linestyles =["-", "--", ":","-", "--", ":","-", "--", ":","-"]第三步,绘制十分类ROC曲线
plt.figure(figsize=(12,5),facecolor='w')
for i in range(10):
roc_auc = 0
#添加文本信息
if i==0:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=1)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.3, 0.01, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==1:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=2)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.3, 0.11, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==2:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=3)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.3, 0.21, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==3:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=4)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.3, 0.31, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==4:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=5)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.3, 0.41, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==5:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=6)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.6, 0.01, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==6:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=7)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.6, 0.11, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==7:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=8)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.6, 0.21, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==8:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=9)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.6, 0.31, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
elif i==9:
fpr, tpr, threshold = roc_curve(y_list,pre_list[i],pos_label=10)
# 计算AUC的值
roc_auc = auc(fpr, tpr)
plt.text(0.6, 0.41, "class "+lable_names[i]+' :ROC curve (area = %0.2f)' % roc_auc)
my_list.append(roc_auc)
# 添加ROC曲线的轮廓
plt.plot(fpr, tpr, color = colors1[i],linestyle = linestyles[i],linewidth = 3,
label = "class:"+lable_names[i]) # lw = 1,
#绘制面积图
plt.stackplot(fpr, tpr, colors=colors2, alpha = 0.5,edgecolor = colors1[i]) # alpha = 0.5,
# 添加对角线
plt.plot([0, 1], [0, 1], color = 'black', linestyle = '--',linewidth = 3)
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
plt.grid()
plt.legend()
plt.title("手机上网稳定性ROC曲线和AUC数值")
plt.show()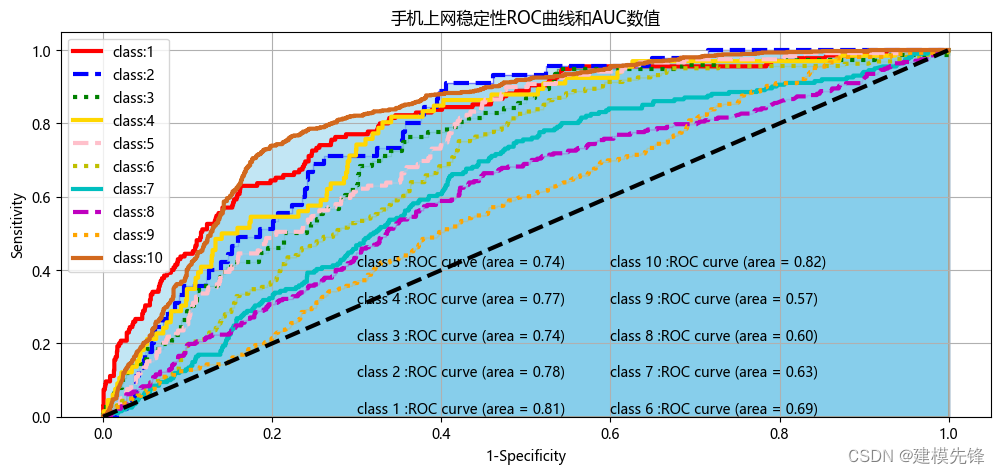
文章来源:https://blog.csdn.net/qq_40949048/article/details/134696419
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
