数据结构--图

? 树具有灵活性，并且存在许多不同的树的应用，但是就树本身而言有一定的局限性，树只能表示层次关系，比如父子关系。而其他的比如兄弟关系只能够间接表示。

推广---? 图

图形结构中，数据元素之间的关系是任意的。

一、图的基本概念

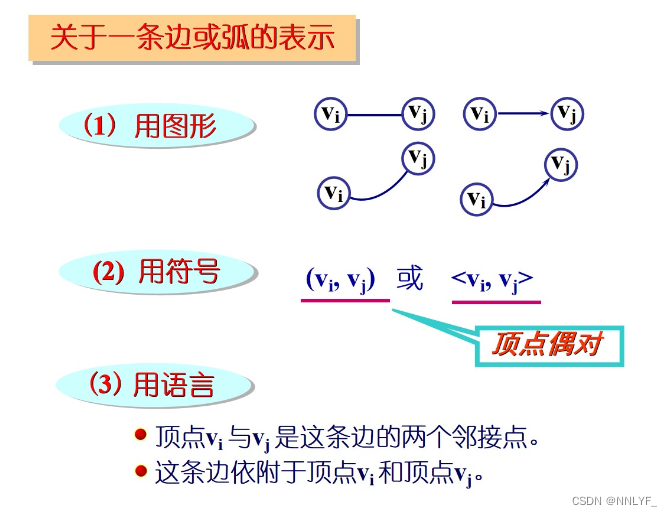
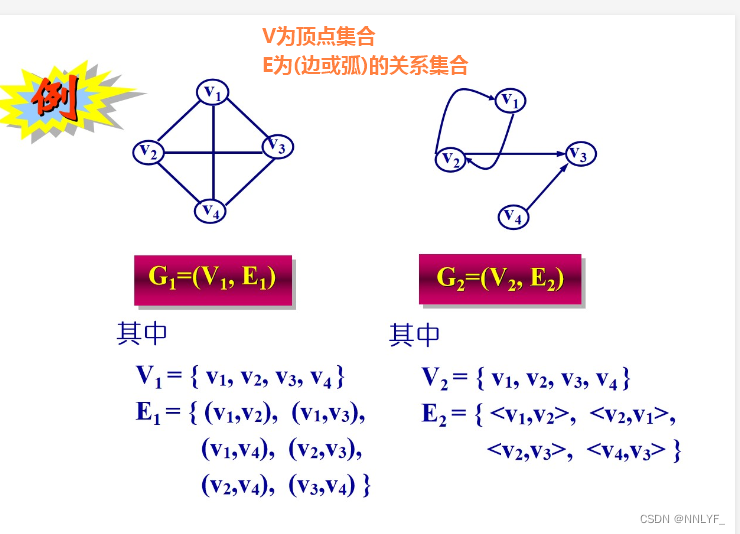
二、图的分类

三、图的相关术语

1、顶点的度

无向图：n个顶点找两条，没有方向，

2、路径和路径长度

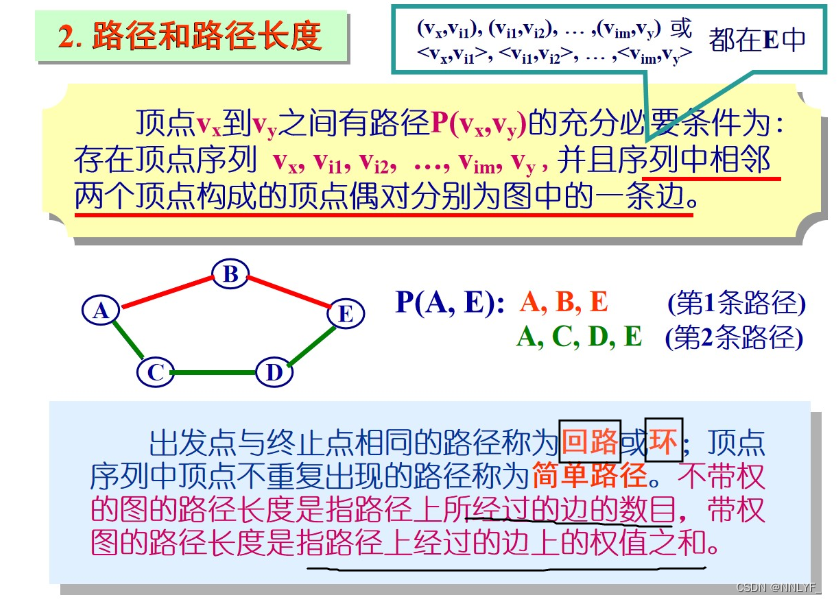
3.子图

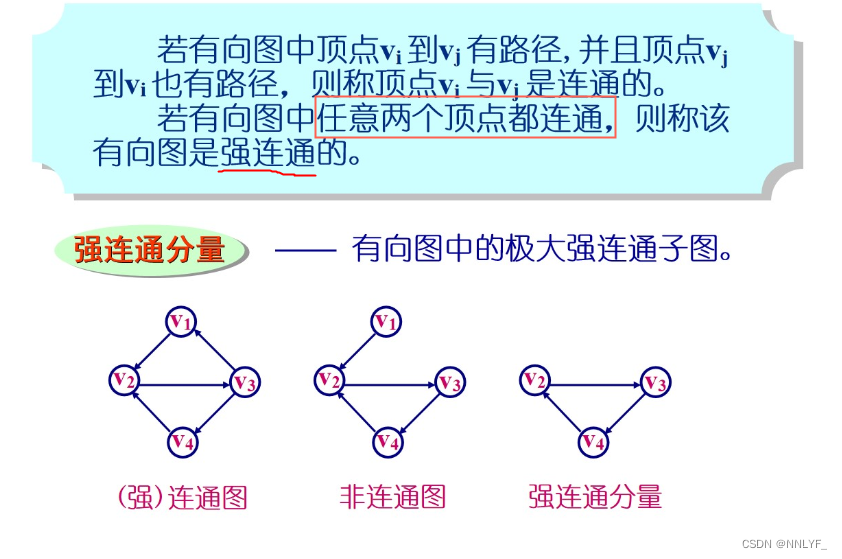
4.图的连通

1）无向图的连通

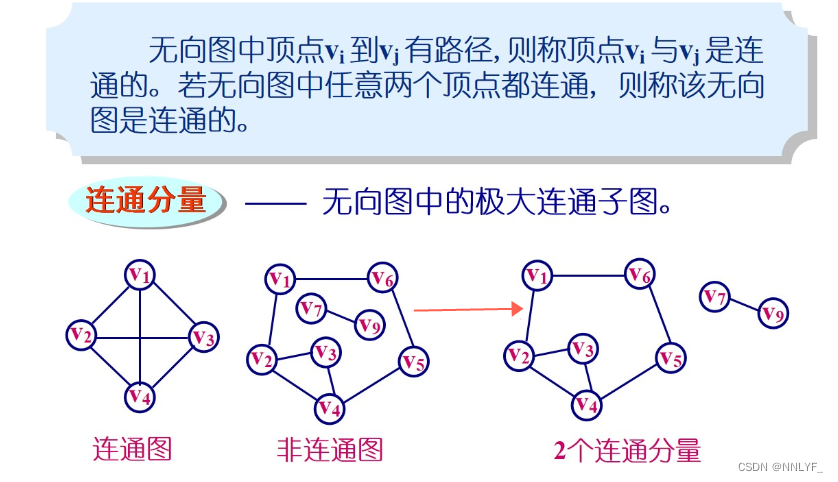
2）有向图的连通

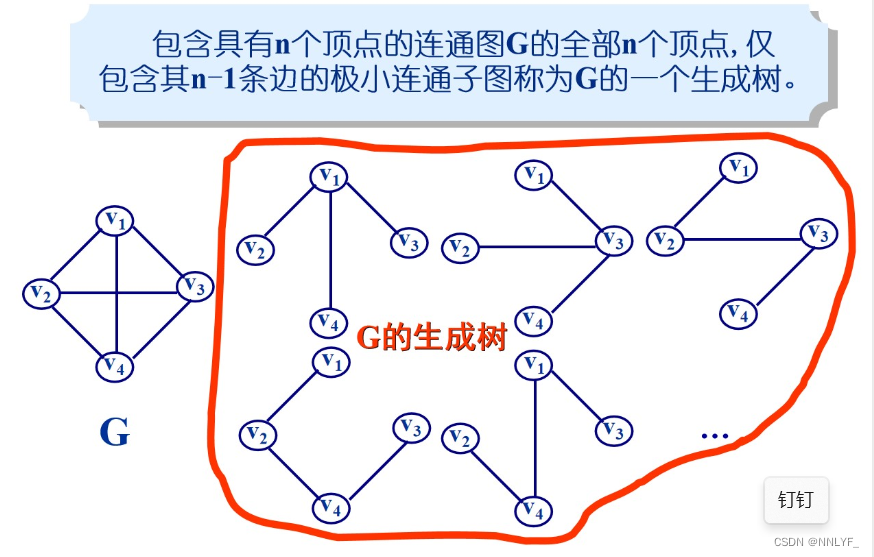
5.生成树

#不讨论的图：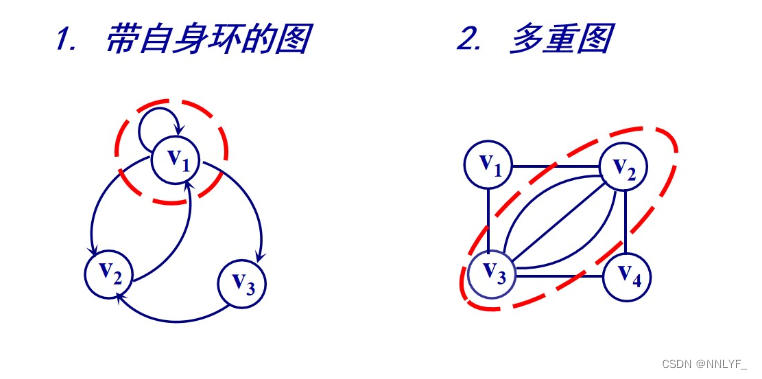

四、图的存储方法

1、邻接矩阵存储方法

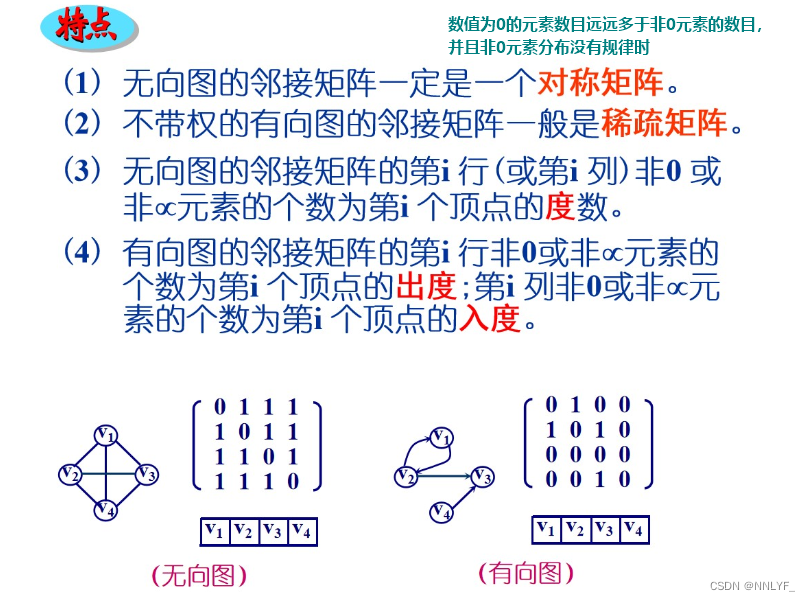
对称矩阵：

一个对称矩阵是指矩阵的主对角线两侧的元素相等。在这个矩阵中，通过观察可以发现对称性质：矩阵的第i行第j列的元素等于第j行第i列的元素。

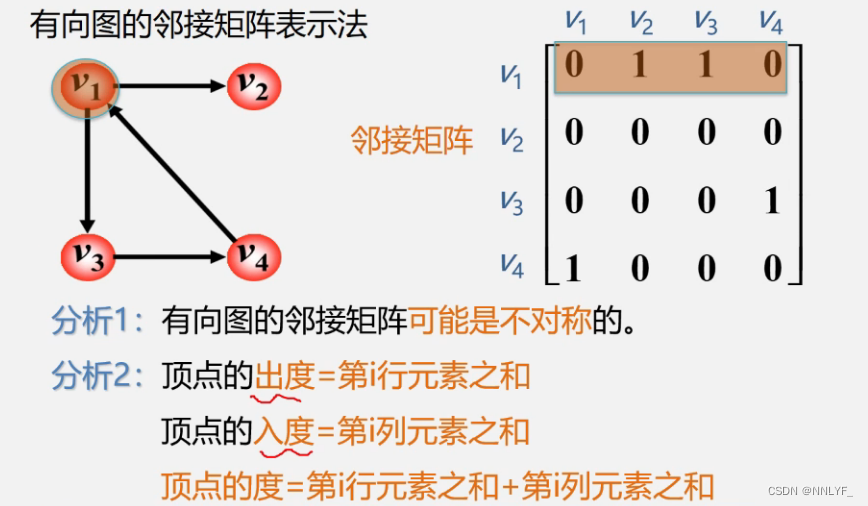
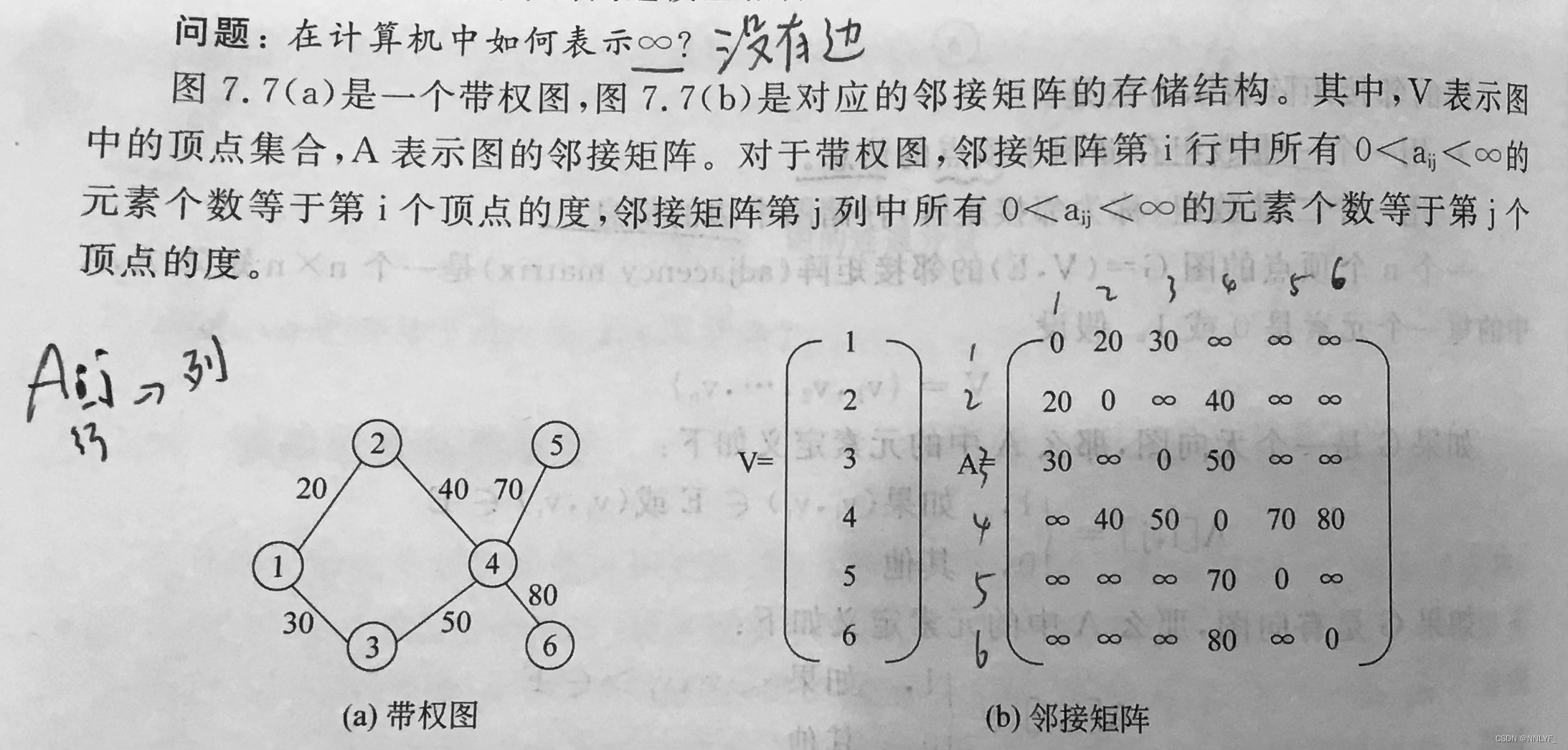
**无向图的邻接矩阵建图和度数输出（完整代码）

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <string.h>
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量

typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型

typedef struct {
    int n, m; //n个顶点，m条边
    VexType vex[N];//一维数组存放所有顶点的数据信息
    EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;

//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息（顶点、邻接矩阵）
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);

int main()
{
    //1.建图
    adjGraph g = createGraph();
    //2.输出图的信息
    print(g);
    printDegree(g);
    return 0;
}

adjGraph createGraph()//建图
{
    adjGraph g;
    memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中，所有元素初始化为0
    // g.edge 邻接矩阵
    //sizeof(g.edge) 数组占用的总字节数
    scanf("%d%d", &g.n, &g.m);//输入顶点数和边数
    getchar();//吸收换行符
    //1.输入n个顶点
    for (int i = 0; i < g.n; i++) {
        scanf("%c ", &g.vex[i]);
    }
    //2.输入m条边，按照邻接矩阵存图
    for (int i = 0; i < g.m; i++) {
        char v1, v2;
        scanf("\n%c %c", &v1, &v2);//读入当前边的2个顶点
        int n1 = v1 - 'A', n2 = v2 - 'A';
         //将顶点字符转换为对应的数组索引。
        // 假设顶点标签是大写字母'A'、'B'、'C'等，通过将其减去字符'A'的ASCII码值
        // 可以得到对应的数组索引（0、1、2等）。   
        g.edge[n1][n2] = g.edge[n2][n1] = 1;
        //无向图，邻接矩阵对应的n1行n2列和n2n1列都赋值为1(邻接矩阵的对称性）
        //将对应的邻接矩阵元素设置为1，表示图中对应的顶点之间存在一条边。
    }

    return g;
}

void print(adjGraph g)
{
    printf("图有%d个顶点，%d条边\n", g.n, g.m);
    printf("图的顶点是：");
    for (int i = 0; i < g.n; i++) {
        printf("%c ", g.vex[i]);
    }
    printf("\n图的邻接矩阵是：\n");
    for (int i = 0; i < g.n; i++) {
        for (int j = 0; j < g.n; j++) {
            printf("%4d", g.edge[i][j]);
        }
        printf("\n");
    }
}

void printDegree(adjGraph g)
{
    printf("图中每个顶点的度数是：");
    for (int i = 0; i < g.n; i++) {
        int degree = 0;
        for (int j = 0; j < g.n; j++) {
            if (g.edge[i][j] == 1) {
                degree++;
            }
        }
        printf("%c: %d ", g.vex[i], degree);
    }
    printf("\n");
}

输入样例：

**有向图邻接矩阵建图和度数输出（附完整代码）

修改的部分：

• 将g.edge[n1][n2] = g.edge[n2][n1] = 1; 修改为 g.edge[n1][n2] = 1; 表示从顶点n1指向顶点n2的有向边。
• 把无向图中的度数输出改成入度和出度输出

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <string.h>
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量

typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型

typedef struct {
    int n, m; //n个顶点，m条边
    VexType vex[N];//一维数组存放所有顶点的数据信息
    EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;

//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息（顶点、邻接矩阵）
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);

int main()
{
    //1.建图
    adjGraph g = createGraph();
    //2.输出图的信息
    print(g);
    printDegree(g);
    return 0;
}

adjGraph createGraph()//建图
{
    adjGraph g;
    memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中，所有元素初始化为0
    // g.edge 邻接矩阵
    //sizeof(g.edge) 数组占用的总字节数
    scanf("%d%d", &g.n, &g.m);//输入顶点数和边数
    getchar();//吸收换行符
    //1.输入n个顶点
    for (int i = 0; i < g.n; i++) {
        scanf("%c ", &g.vex[i]);
    }
    //2.输入m条边，按照邻接矩阵存图
    for (int i = 0; i < g.m; i++) {
        char v1, v2;
        scanf("\n%c %c", &v1, &v2);//读入当前边的2个顶点
        int n1 = v1 - 'A', n2 = v2 - 'A';
        //将顶点字符转换为对应的数组索引。
       // 假设顶点标签是大写字母'A'、'B'、'C'等，通过将其减去字符'A'的ASCII码值
       // 可以得到对应的数组索引（0、1、2等）。   
        g.edge[n1][n2] = 1;
        //有向图，邻接矩阵对应的n1行n2列赋值为1
        //将对应的邻接矩阵元素设置为1，表示图中对应的顶点之间存在一条边。
    }

    return g;
}

void print(adjGraph g)
{
    printf("图有%d个顶点，%d条边\n", g.n, g.m);
    printf("图的顶点是：");
    for (int i = 0; i < g.n; i++) {
        printf("%c ", g.vex[i]);
    }
    printf("\n图的邻接矩阵是：\n");
    for (int i = 0; i < g.n; i++) {
        for (int j = 0; j < g.n; j++) {
            printf("%4d", g.edge[i][j]);
        }
        printf("\n");
    }
}

void printDegree(adjGraph g)
{
    printf("图中每个顶点的入度是：\n");
    for (int i = 0; i < g.n; i++) {
        int indegree = 0;
            for (int j = 0; j < g.n; j++) {
                if (g.edge[j][i] == 1) {
                    indegree++;
                 }
            }
            printf("%c: %d \n", g.vex[i], indegree);
       }
       
  


    printf("图中每个顶点的出度是：\n");
    for (int i = 0; i < g.n; i++) {
        int outdegree = 0;
        for (int j = 0; j < g.n; j++) {
            if (g.edge[i][j] == 1) {
                outdegree++;
            }
        }
        printf("%c: %d \n", g.vex[i], outdegree);
        
    }

}

测试样例：

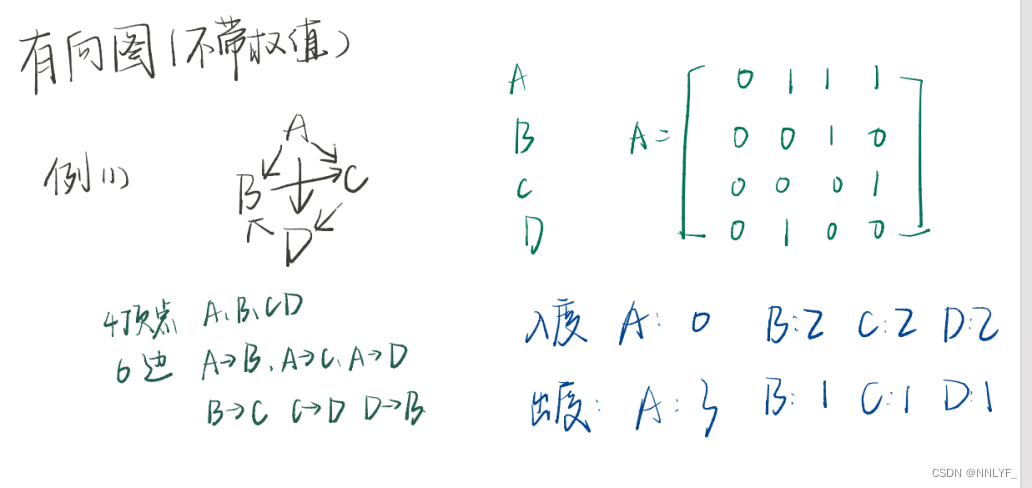
**有向带权图邻接矩阵建图和度数输出（含完整代码）

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <string.h>
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量

typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型

typedef struct {
    int n, m; //n个顶点，m条边
    VexType vex[N];//一维数组存放所有顶点的数据信息
    EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;

//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息（顶点、邻接矩阵）
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);

int main()
{
    //1.建图
    adjGraph g = createGraph();
    //2.输出图的信息
    print(g);
    printDegree(g);
    return 0;
}


adjGraph createGraph()//建图
{
    adjGraph g;
    memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中，所有元素初始化为0
    // g.edge 邻接矩阵
    //sizeof(g.edge) 数组占用的总字节数
    scanf("%d%d", &g.n, &g.m);//输入顶点数和边数
    getchar();//吸收换行符
    //1.输入n个顶点
    for (int i = 0; i < g.n; i++) {
        scanf("%c ", &g.vex[i]);
    }
    //2.输入m条边，按照邻接矩阵存图 
    // 将邻接矩阵初始化为INF
    for (int i = 0; i < g.m; i++) {
        for (int j = 0; j < g.m; j++) {
            g.edge[i][j] = INF;
        }
    }
    for (int i = 0; i < g.m; i++) {
        char v1, v2;
        int weight;
        scanf("\n%c %d %c", &v1, &weight, &v2);//读入当前边的2个顶点
        int n1 = v1 - 'A', n2 = v2 - 'A';
        //将顶点字符转换为对应的数组索引。
        // 假设顶点标签是大写字母'A'、'B'、'C'等，通过将其减去字符'A'的ASCII码值
        // 可以得到对应的数组索引（0、1、2等）。
       
        if (n1 == n2) {
            g.edge[n1][n2] = 0;
        }
        else {
            g.edge[n1][n2] = weight;
            g.edge[n2][n1] = INF; // 反方向的边权值设置为INF
        }
    }


    return g;
}

void print(adjGraph g)
{
    printf("图有%d个顶点，%d条边\n", g.n, g.m);
    printf("图的顶点是：");
    for (int i = 0; i < g.n; i++) {
        printf("%c ", g.vex[i]);
    }
    printf("\n图的邻接矩阵是：\n");
    for (int i = 0; i < g.n; i++) {
        for (int j = 0; j < g.n; j++) {
            if (i == j) printf("0 ");
            else if (g.edge[i][j] == INF)
            {
                printf("INF ");
           }
            else  {
                   printf("%-4d", g.edge[i][j]);
            }
                  
        
            
        }
        printf("\n");
    }
}

void printDegree(adjGraph g)
{
    printf("图中每个顶点的入度是：\n");
    for (int i = 0; i < g.n; i++) {
        int indegree = 0;
        for (int j = 0; j < g.n; j++) {
     
                  if (g.edge[j][i] != 0 && g.edge[j][i] != INF) {
                     indegree++;
                 }
    
            
        }
        printf("%c: %d \n", g.vex[i], indegree);
    }




    printf("图中每个顶点的出度是：\n");
    for (int i = 0; i < g.n; i++) {
        int outdegree = 0;
        for (int j = 0; j < g.n; j++) {
                if (g.edge[i][j] != 0&& g.edge[i][j] != INF) {
                    outdegree++;
                }
            }

        
        printf("%c: %d \n", g.vex[i], outdegree);

    }

}

样例：

2、邻接表存储方法

? 对每一个顶点建立一个单链表，将同一个顶点发出的边链接在一个称为边链表的单链表中。

头插法：

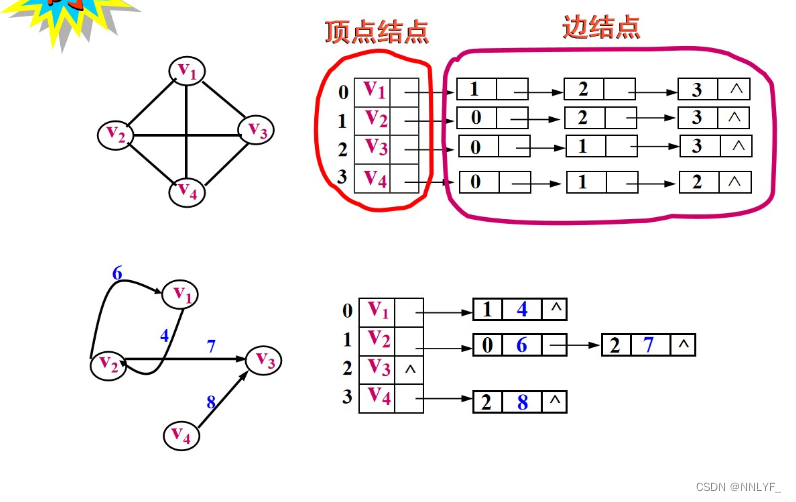
五、图的遍历

六、最小生成树

? ? ??

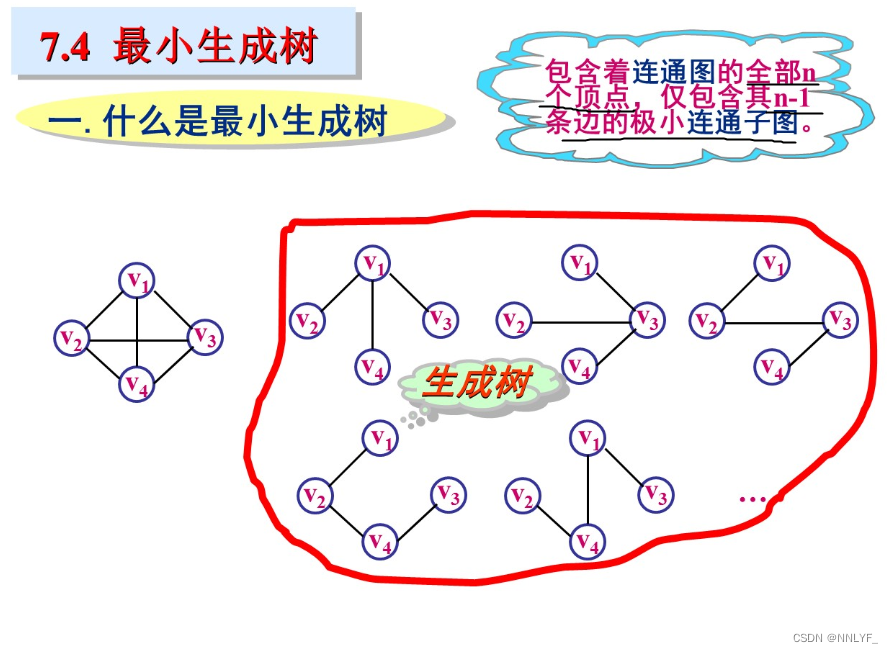
七、最短路径问题

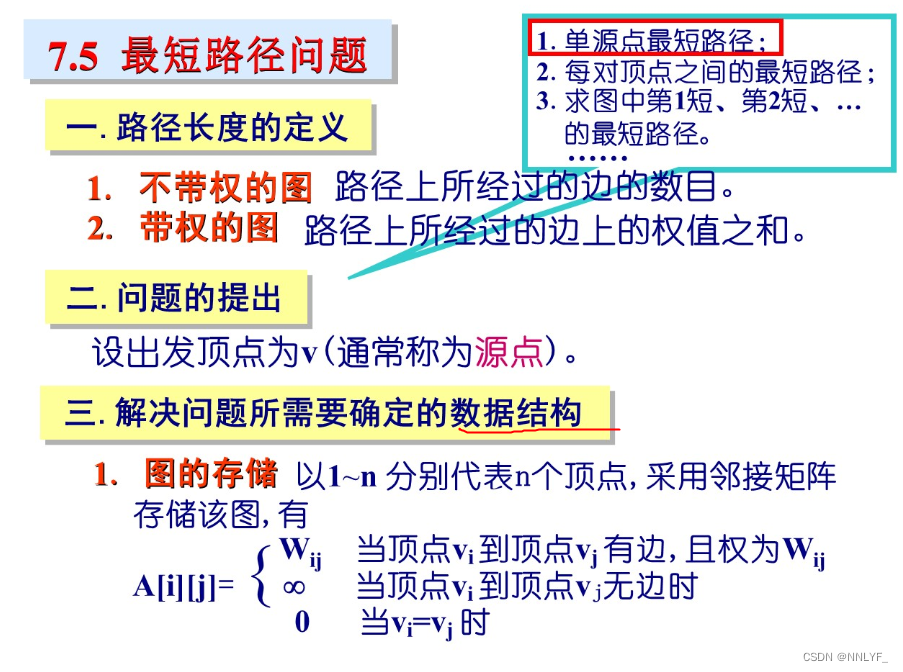
八、AOV网与拓扑排序

九、AOE网与关键路径