Linear Regression多重共线性
2023-12-19 20:56:55
目录
介绍:
多重共线性是指在线性回归模型中,自变量之间存在强相关性或线性关系,从而导致模型的稳定性和可解释性受到影响。
在线性回归中,我们希望自变量与因变量之间有一定的线性关系,且自变量之间尽可能不相关,这样可以更好地解释因变量的变化。然而,当自变量之间存在强相关性时,模型很难区分各自变量对因变量的独立贡献,导致估计结果不准确。
多重共线性会对线性回归模型产生以下影响:
1. 估计值不稳定:由于自变量之间存在强相关性,小的变动可能导致估计值发生较大变化,使得模型不稳定。
2. 估计值偏离:多重共线性会导致估计值偏离真实值,造成参数估计的失准。
3. 可解释性下降:由于自变量之间存在强相关性,我们无法准确判断每个自变量对因变量的独立贡献,从而降低了模型的可解释性。为了解决多重共线性问题,可以采取以下方法:
1. 使用岭回归或Lasso回归:这些方法通过对系数加上惩罚项,可以减小系数估计值的方差,从而减轻多重共线性带来的影响。
2. 特征选择:通过选择具有较高解释性和较低相关性的自变量,可以降低多重共线性的影响。
3. 增加样本量:增加样本量可以减小参数估计的方差,从而降低多重共线性的影响。总之,多重共线性是线性回归模型中常见的问题,会影响模型的稳定性和可解释性。通过合适的方法处理多重共线性,可以改善模型的效果并得到准确的估计结果。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns#多元共线性是指多元回归模型中两个或多个变量高度线性相关的情况,当回归模型中的自变量相互关联时,就会出现多重共线性,因为自变量应该是独立的,如果变量之间的相关程度足够高,那么在拟合模型和解释结果时就会出现问题
df=pd.read_csv('50_Startups.csv')
df.head()
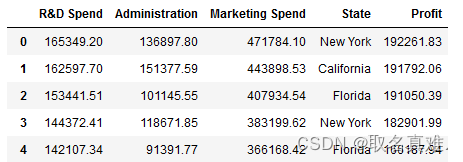 ?
?
一、?corr
df.corr()#相关性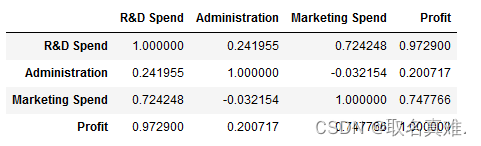
X=X1=df.iloc[:,:-2]#取前三行为自变量
X.head()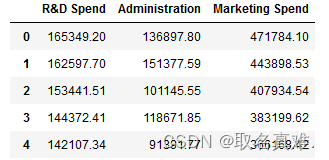 ?二、pairplot?
?二、pairplot?
sns.pairplot(X)#两两对比,可以看到R&D Spend和Marketing Spend相关性高 ?
?
三、VIF
3.1自带vif
from statsmodels.stats.outliers_influence import variance_inflation_factor
variance_inflation_factor(X.values,0)#第一项的共线性
#结果:8.384570754559961
variance_inflation_factor(X.values,1)#第二项的共线性
#结果:4.0264055178945535
variance_inflation_factor(X.values,2)#第三项的共线性
#结果:7.593983592680924
?3.2自定义函数vif
def vif(X):
vif=pd.DataFrame()
vif["variables"]=X.columns
vif["VIF"]=[variance_inflation_factor(X.values,i) for i in range(X.shape[1])]
return(vif)
vif(X)#共线性分析
X=X.drop('R&D Spend',axis=1)#去掉R&D Spend
vif(X)#共线性降低

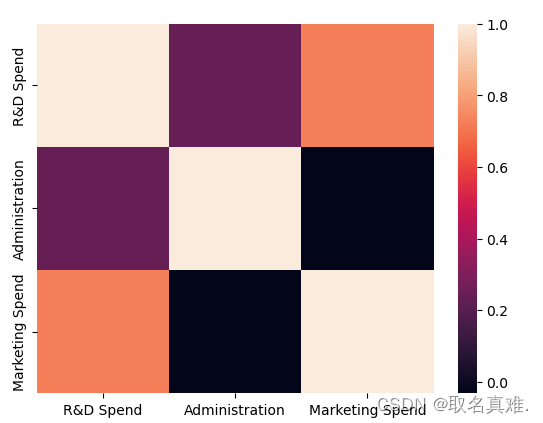
四、heatmp(直观感受)
X1.corr()
sns.heatmap(X1.corr())#热图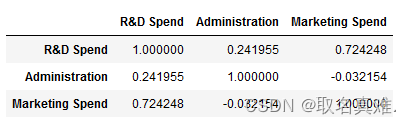
文章来源:https://blog.csdn.net/qq_74156152/article/details/135089883
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!