李沐机器学习系列4---全连接层到卷积
1 从全连接到卷积

1.1 平移不变性

从概率分布的角度来看卷积的定义,
f
(
τ
)
f(\tau)
f(τ)是概率密度,
g
(
t
?
τ
)
g(t-\tau)
g(t?τ)是在这个分布下的均值
(
f
?
g
)
(
t
)
=
∫
?
∞
∞
f
(
τ
)
g
(
t
?
τ
)
d
τ
(f*g)(t)=\int_{-\infin}^{\infin}f(\tau)g(t-\tau)d\tau
(f?g)(t)=∫?∞∞?f(τ)g(t?τ)dτ

2 图像卷积
2.1 互相关运算
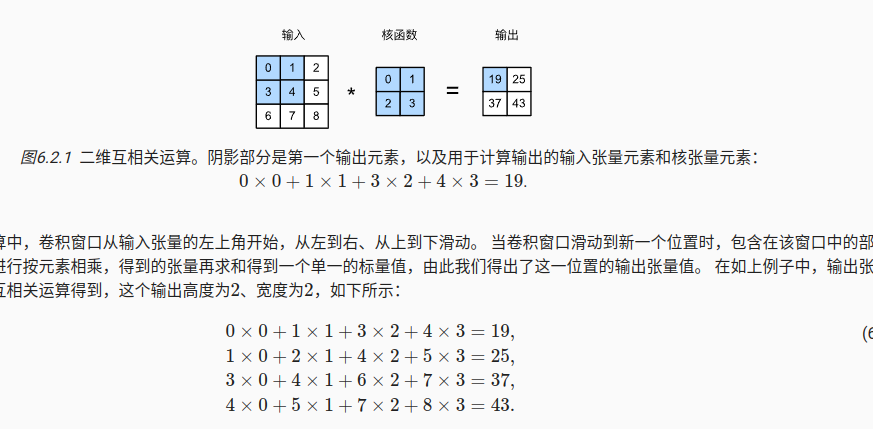
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): #@save
"""计算二维互相关运算"""
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Y
2.2 特征影射和感受野
特征映射(feature map),因为它可以被视为一个输入映射到下一层的空间维度的转换器。 在卷积神经网络中,对于某一层的任意元素,其感受野(receptive field)是指在前向传播期间可能影响计算的所有元素(来自所有先前层)。
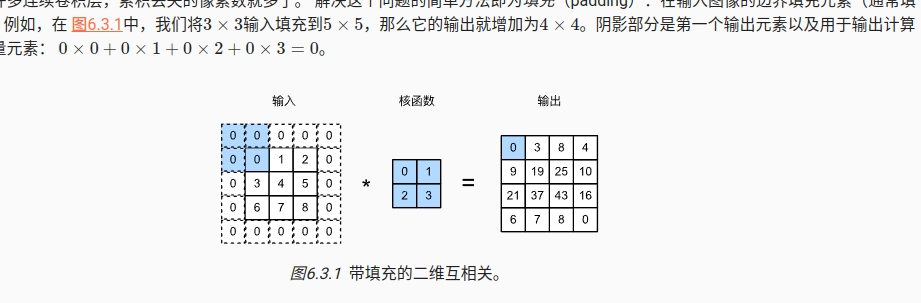
3 填充
边界进行0填充,主要是autograd如何解决,前向比较容易实现
import torch
from torch import nn
# 为了方便起见,我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重,并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
# 这里的(1,1)表示批量大小和通道数都是1
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
# 省略前两个维度:批量大小和通道
return Y.reshape(Y.shape[2:])
# 请注意,这里每边都填充了1行或1列,因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape
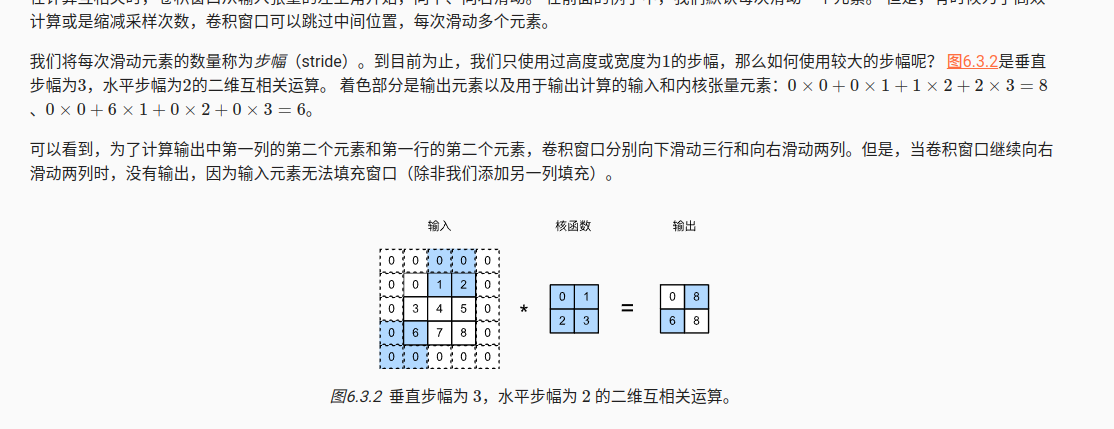
4 多输入多输出通道
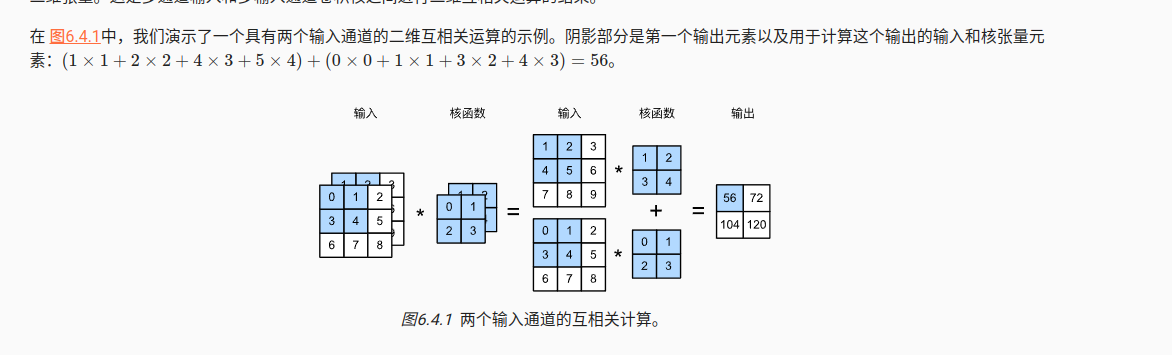
4.1 多输入通道
输入通道数量c_i对应核的维度
4.2 多输出通道

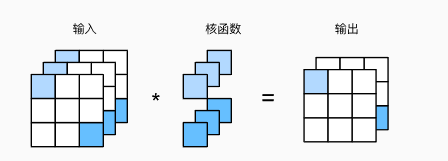
4.3 1*1卷积层
改变输入的通道数量,但是保持相同的高度和宽度
5 汇聚层
最后一层的神经元应该对整个输入的全局敏感。通过逐渐聚合信息,生成越来越粗糙的映射,最终实现学习全局表示的目标,同时将卷积图层的所有优势保留在中间层
汇聚层的两个作用:
- 降低卷积层对位置的敏感性
- 降低对空间降采样表示的敏感性
5.1 最大汇聚层和平均汇聚层

5.2 多个通道
多个通道对每个通道进行单独计算,不会进行汇总。
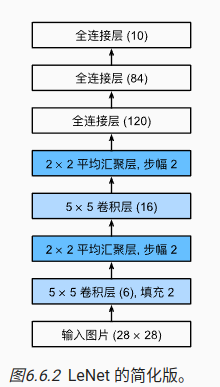
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))
6 AlexNet
6.1 早期的图像发展历程

通过神经网络学习特征

突破的关键要素:
1)数据
2)硬件
AlexNet
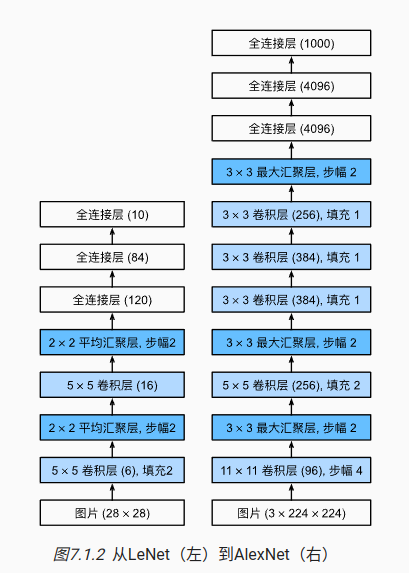
改进方法:
1)网络维度更大,参数接近1G
2)激活函数,更换成Relu
3) 容量控制和预处理
使用图像增强,翻转,裁切,和变色
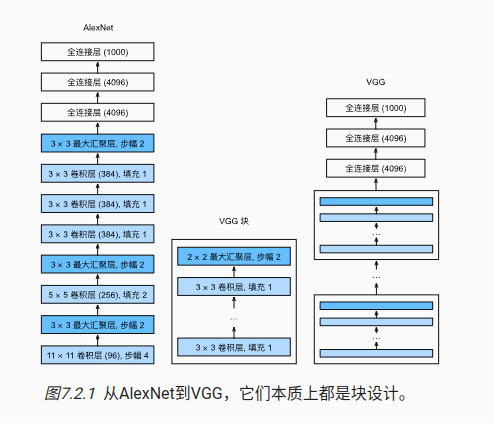
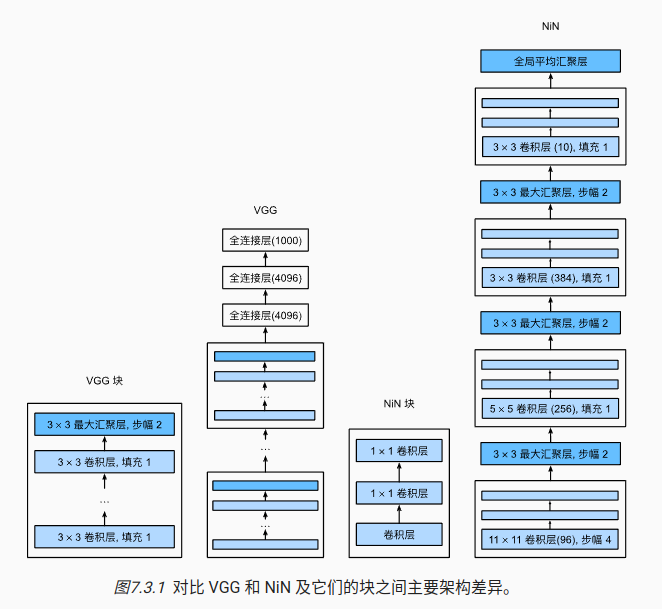
8 VGG
出现了代码块,将一些可以复用的网络结构进行封装
import torch
from torch import nn
from d2l import torch as d2l
def vgg_block(num_convs, in_channels, out_channels):
layers = []
for _ in range(num_convs):
layers.append(nn.Conv2d(in_channels, out_channels,
kernel_size=3, padding=1))
layers.append(nn.ReLU())
in_channels = out_channels
layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
return nn.Sequential(*layers)
也可以使用pytorch的自定义块功能
import torch
from torch import nn
class VGGBlock(nn.Module):
def __init__(self, num_convs, in_channels, out_channels):
super(VGGBlock, self).__init__()
layers = []
for _ in range(num_convs):
layers.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
layers.append(nn.ReLU())
in_channels = out_channels
layers.append(nn.MaxPool2d(kernel_size=2, stride=2))
self.vgg_block = nn.Sequential(*layers)
def forward(self, x):
return self.vgg_block(x)
9 NiN块
核心的思想:
1)取消了全连接层,最后用一个全局平均汇聚层,生成对数几率
2)使用串联网络
import torch
from torch import nn
from d2l import torch as d2l
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())
net = nn.Sequential(
nin_block(1, 96, kernel_size=11, strides=4, padding=0),
nn.MaxPool2d(3, stride=2),
nin_block(96, 256, kernel_size=5, strides=1, padding=2),
nn.MaxPool2d(3, stride=2),
nin_block(256, 384, kernel_size=3, strides=1, padding=1),
nn.MaxPool2d(3, stride=2),
nn.Dropout(0.5),
# 标签类别数是10
nin_block(384, 10, kernel_size=3, strides=1, padding=1),
nn.AdaptiveAvgPool2d((1, 1)),
# 将四维的输出转成二维的输出,其形状为(批量大小,10)
nn.Flatten())
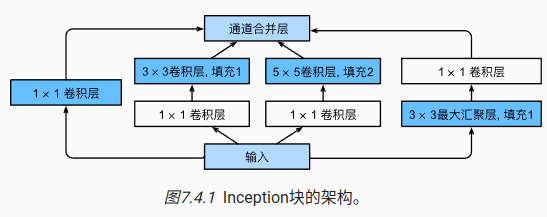
10 GoogleNet
核心思想:
1)使用不同大小的卷积核组合是有利的
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Inception(nn.Module):
# c1--c4是每条路径的输出通道数
def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
super(Inception, self).__init__(**kwargs)
# 线路1,单1x1卷积层
self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
# 线路2,1x1卷积层后接3x3卷积层
self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
# 线路3,1x1卷积层后接5x5卷积层
self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
# 线路4,3x3最大汇聚层后接1x1卷积层
self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)
def forward(self, x):
p1 = F.relu(self.p1_1(x))
p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
p4 = F.relu(self.p4_2(self.p4_1(x)))
# 在通道维度上连结输出
return torch.cat((p1, p2, p3, p4), dim=1)
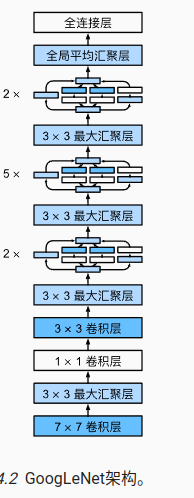
11 批量规范化
训练网络的一些关键挑战:
1)标准化输入特征
2)中间变量,这些变量分布中的这种偏移可能会阻碍网络的收敛,
3)更深层的网络很复杂,容易过拟合。 这意味着正则化变得更加重要

11.1 批量规范化应用在全连接层

import torch
from torch import nn
from d2l import torch as d2l
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。
# 这里我们需要保持X的形状以便后面可以做广播运算
mean = X.mean(dim=(0, 2, 3), keepdim=True)
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
# 训练模式下,用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 缩放和移位
return Y, moving_mean.data, moving_var.data
定义一个BatchNOorm, 因为batchNorm中的gamma和beta这两个参数是需要再训练中进行更新的,
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
nn.Linear(84, 10))
标准的batchNorm的实现
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
nn.Linear(84, 10))
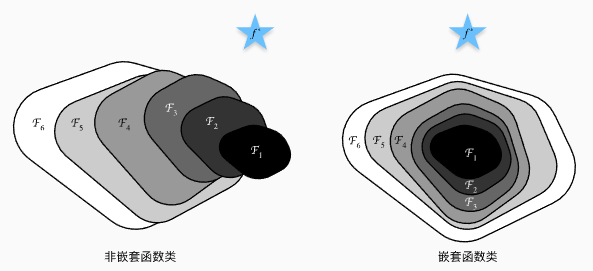
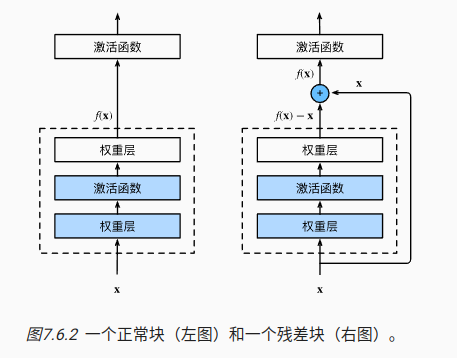
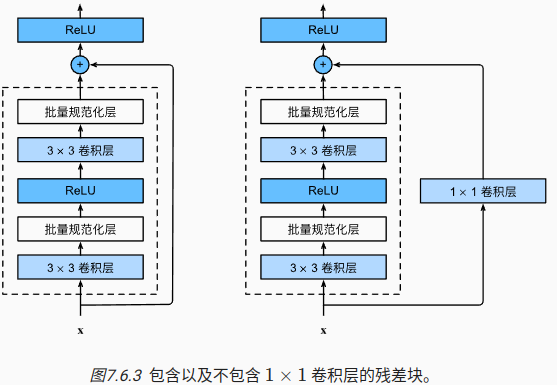
12 Resnet
使用嵌套函数来理解Resnet的作用,每个附加层都应该更容易地包含原始函数作为其元素之一
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Residual(nn.Module): #@save
def __init__(self, input_channels, num_channels,
use_1x1conv=False, strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels,
kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels,
kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return F.relu(Y)
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
def resnet_block(input_channels, num_channels, num_residuals,
first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(Residual(input_channels, num_channels,
use_1x1conv=True, strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))
net = nn.Sequential(b1, b2, b3, b4, b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(), nn.Linear(512, 10))
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape:\t', X.shape)
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
12 DenseNet
思路来源于函数的泰勒展开,


import torch
from torch import nn
from d2l import torch as d2l
def conv_block(input_channels, num_channels):
return nn.Sequential(
nn.BatchNorm2d(input_channels), nn.ReLU(),
nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))
class DenseBlock(nn.Module):
def __init__(self, num_convs, input_channels, num_channels):
super(DenseBlock, self).__init__()
layer = []
for i in range(num_convs):
layer.append(conv_block(
num_channels * i + input_channels, num_channels))
self.net = nn.Sequential(*layer)
def forward(self, X):
for blk in self.net:
Y = blk(X)
# 连接通道维度上每个块的输入和输出
X = torch.cat((X, Y), dim=1)
return X
blk = DenseBlock(2, 3, 10)
X = torch.randn(4, 3, 8, 8)
Y = blk(X)
Y.shape
def transition_block(input_channels, num_channels):
return nn.Sequential(
nn.BatchNorm2d(input_channels), nn.ReLU(),
nn.Conv2d(input_channels, num_channels, kernel_size=1),
nn.AvgPool2d(kernel_size=2, stride=2))
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!