MIT18.06线性代数 笔记3
对称矩阵及正定性
- 特征值是实数
- 特征向量垂直=>标准正交
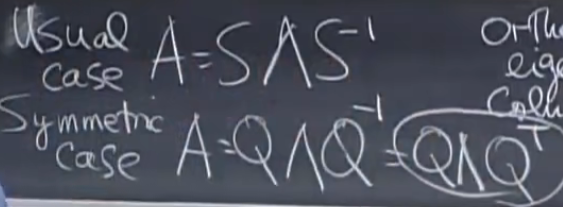
谱定理,主轴定理
为什么对称矩阵的特征值是实数:
对特征值和特征向量取共轭(A是实数矩阵,共轭后不变)
A
x
=
λ
x
x
 ̄
T
A
x
=
λ
x
 ̄
T
x
?
取共轭
A
x
 ̄
=
λ
 ̄
x
 ̄
?
转置
x
 ̄
T
A
=
x
 ̄
T
λ
 ̄
x
 ̄
T
A
x
=
x
 ̄
T
λ
 ̄
x
可知
λ
x
 ̄
T
x
=
x
 ̄
T
λ
 ̄
x
,即
λ
=
λ
 ̄
\begin{aligned} \begin{aligned} Ax &= \lambda x \\ \overline{x}^TAx &= \lambda\overline{x}^Tx \end{aligned} \Rightarrow^{取共轭} A\overline{x}=\overline{\lambda}\overline{x} \Rightarrow^{转置} \begin{aligned} \overline{x}^TA &= \overline{x}^T\overline{\lambda} \\ \overline{x}^TAx &= \overline{x}^T\overline{\lambda}x \end{aligned}\\ 可知\lambda\overline{x}^Tx=\overline{x}^T\overline{\lambda}x,即\lambda=\overline{\lambda} \end{aligned}
AxxTAx?=λx=λxTx??取共轭Ax=λx?转置xTAxTAx?=xTλ=xTλx?可知λxTx=xTλx,即λ=λ?
如果一个向量为复向量,那么 x  ̄ T x 就是其长度的平方 如果一个向量为复向量,那么\overline{x}^Tx就是其长度的平方 如果一个向量为复向量,那么xTx就是其长度的平方

q
1
q
1
T
类似于
P
=
a
a
T
a
T
a
,是投影矩阵
q_1q_1^T类似于P=\frac{aa^T}{a^Ta},是投影矩阵
q1?q1T?类似于P=aTaaaT?,是投影矩阵
所以,每个对称矩阵都是一些相互垂直的投影矩阵的组合
对对称矩阵来说,正主元的个数=正特征值的个数,通过这个结论,可以缩小特征值的范围:将矩阵平移7倍的单位矩阵,即将特征值平移7,计算矩阵主元,从而直到原矩阵多少特征值大于7多少小于7
对称矩阵主元的乘积=对称矩阵的行列式=特征值的乘积
正定矩阵:
- 所有特征值为正
- 所有主元为正
- 所有的子行列式(左上到右下)为正
复数矩阵和快速傅里叶变换
复向量模长度:
z
 ̄
T
z
=
z
H
z
=
[
z
1
 ̄
z
2
 ̄
…
z
n
 ̄
]
[
z
1
z
2
…
z
n
]
=
∣
z
1
∣
2
+
∣
z
2
∣
2
+
∣
z
3
∣
2
+
?
+
∣
z
n
∣
2
=
向量模长平方
\overline{z}^Tz= z^Hz= \begin{bmatrix} \overline{z_1} & \overline{z_2} & \dots & \overline{z_n} \end{bmatrix} \begin{bmatrix} z_1\\ z_2\\ \dots\\ z_n \end{bmatrix}=|z_1|^2+|z_2|^2+|z_3|^2+\dots+|z_n|^2=向量模长平方
zTz=zHz=[z1???z2???…?zn???]
?z1?z2?…zn??
?=∣z1?∣2+∣z2?∣2+∣z3?∣2+?+∣zn?∣2=向量模长平方
复向量内积:
y
 ̄
T
x
=
y
H
x
\overline{y}^Tx=y^Hx
y?Tx=yHx
复对称矩阵(埃尔米特矩阵):
A
 ̄
T
=
A
H
=
A
\overline{A}^T=A^H=A
AT=AH=A
这些矩阵的特征值是实数,特征向量相互垂直,即内积为:
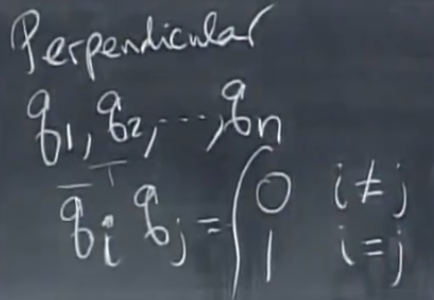
Q
 ̄
T
Q
=
Q
H
Q
=
I
\overline{Q}^TQ=Q^HQ=I
Q?TQ=QHQ=I
Q的逆是QH,这样的正交矩阵称为酉矩阵
傅里叶矩阵:
右边的列元素等于左边的列元素乘第二列对应行的元素
在复平面中,w在单位圆上,每次乘w在图像上都是旋转固定角度由此可根据欧拉公式
e
π
j
=
cos
?
π
+
sin
?
π
j
=
?
1
e^{\pi j}=\cos \pi + \sin \pi j=-1
eπj=cosπ+sinπj=?1
得到具体值
得到的F(n)各列正交,内积(取共轭)为0,
(
w
64
)
2
=
(
e
i
2
π
64
)
2
=
w
32
(w_{64})^2=(e^{i\frac{2\pi}{64}})^2=w_{32}
(w64?)2=(ei642π?)2=w32?
快速傅里叶变换:

计算步骤从642变成2(32)2+32,因为两个F32需要2(32)2,而两个D需要2 * 16。之后继续分解两个F32为四个F16,计算步骤变成2[2(16)2+16]+32,以此类推,最终变成6 * 64,即log264 * (64/2),所以变换后计算步骤能从n2变成nlog2n/2
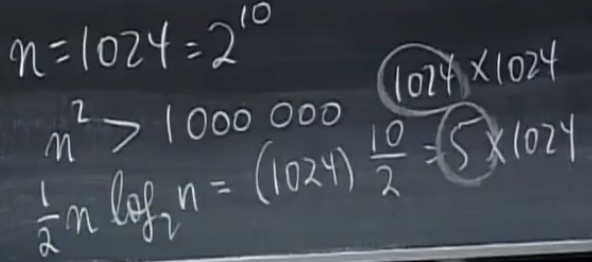
正定矩阵和最小值
正定矩阵的新性质:二次型xTAx > 0
半正定矩阵:行列式正好等于0,即有一个特征值等于0
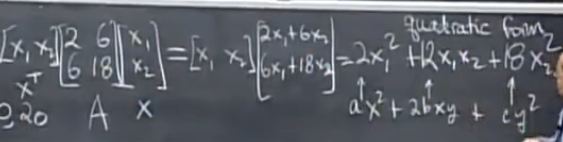
如果是非正定矩阵,如结果为2x12+12x1x2+7x22,该函数图像为鞍面(一个方向上有最大值且小于零,另一方向上有最小值且大于零,原点为鞍点)
如果是正定矩阵,如结果为2x12+12x1x2+20x22,该函数图像为碗面,最小值为原点
微积分:一阶导数等于0,二阶导数大于0=>极小值
线性代数:对f(x1, x2, …),产生它的矩阵A为正定矩阵=>极小值
配方法就是消元:
矩阵
[
2
6
6
20
]
求
x
T
A
x
得
f
(
x
,
y
)
=
2
x
3
+
12
x
y
+
20
y
2
消元得
=
2
(
x
+
3
y
)
2
+
2
y
2
?
第一行主元
(
x
+
消元倍数
y
)
2
+
第二行主元
y
2
矩阵\begin{bmatrix} 2 & 6\\ 6 & 20 \end{bmatrix} 求x^TAx得 \begin{aligned} f(x, y) &= 2x^3+12xy+20y^2\\ 消元得&= 2(x+3y)^2+2y^2 \Rightarrow 第一行主元(x+消元倍数y)^2+第二行主元y^2 \end{aligned}
矩阵[26?620?]求xTAx得f(x,y)消元得?=2x3+12xy+20y2=2(x+3y)2+2y2?第一行主元(x+消元倍数y)2+第二行主元y2?
因此,正主元使得f(x, y)>0,函数图像向上
3x3的例子:

有3x3正定矩阵Q Lambda QT=A(主轴定理),对xTAx取1,得到一个椭球体的函数,椭球体的三个轴方向即A的特征向量方向,轴长度为特征值大小
相似矩阵和若尔当形
A是正定矩阵,因为A-1特征值是A的特征值的倒数,所以也是正定矩阵
A,B是正定矩阵,xT(A+B)x>0,所以A+B也是正定矩阵
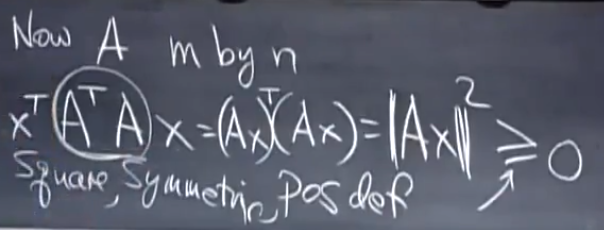
当A的秩是n时,Ax的零空间没有向量,则|Ax|2 > 0
相似矩阵:A和B是相似矩阵,意味着存在矩阵M,使得B=M-1AM
S
?
1
A
S
=
Λ
即
A
、
B
和
Λ
相似
S^{-1}AS=\Lambda\\ 即A、B和\Lambda相似
S?1AS=Λ即A、B和Λ相似
所以存在一个矩阵族,任意两个矩阵互相相似
相似矩阵之间特征值相同
证明:
A
x
=
λ
x
M
?
1
A
M
M
?
1
x
=
λ
M
?
1
x
(
M
?
1
A
M
)
(
M
?
1
x
)
=
λ
(
M
?
1
x
)
B
M
?
1
x
=
λ
M
?
1
x
\begin{aligned} Ax &= \lambda x\\ M^{-1}AMM^{-1}x &= \lambda M^{-1}x\\ (M^{-1}AM)(M^{-1}x) &= \lambda (M^{-1}x)\\ BM^{-1}x &= \lambda M^{-1}x \end{aligned}
AxM?1AMM?1x(M?1AM)(M?1x)BM?1x?=λx=λM?1x=λ(M?1x)=λM?1x?
A和B特征值相同,但是特征向量不同,B的特征向量是 M^{-1}x
当是退化矩阵时,分两种情况:相似矩阵只有它一个矩阵、相似矩阵有多个

第二种叫做若尔当标准型,无法对角化
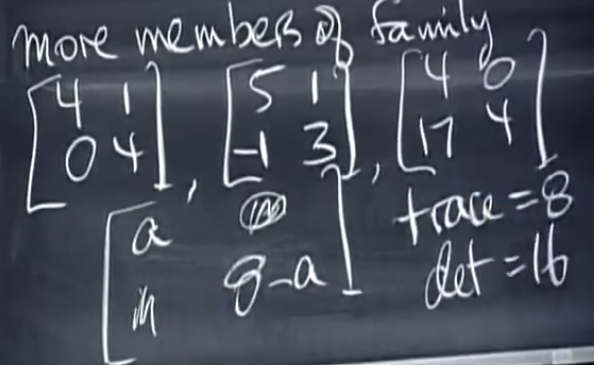
每个A和一个若尔当矩阵相似,若尔当矩阵是由若尔当块构成的矩阵
J
=
[
J
1
J
2
…
J
d
]
J=\begin{bmatrix} J_1 & & & \\ & J_2 & & \\ & & \dots &\\ & & & J_d \end{bmatrix}
J=
?J1??J2??…?Jd??
?
若尔当块:特征值位于对角线上,对角线上方还有若干个1
若A有n个各不相同的特征值,即可对角化,那么对应的若尔当阵就是对角阵 Lambda ,d=n
奇异值分解
SVD对任意A成立
A
=
U
Σ
V
T
A=U\Sigma V^T
A=UΣVT
如A=Q Lambda QT,
行空间的一组正交基变换成一组列空间的正交基,如v1变换成u1就是
σ
1
u
1
=
A
v
1
整合成矩阵就是
A
[
v
1
v
2
…
v
r
v
r
+
1
…
v
n
]
=
[
u
1
u
2
…
u
r
u
r
+
1
…
u
m
]
[
σ
1
…
0
0
…
0
…
…
…
…
…
…
0
…
σ
r
0
…
0
0
…
0
0
…
0
…
…
…
…
…
…
0
…
0
0
…
0
]
A
V
=
U
Σ
\sigma_1u_1=Av_1\\ 整合成矩阵就是\\ \begin{aligned} A\begin{bmatrix} v_1 & v_2 & \dots & v_r & v_{r+1} & \dots & v_n \end{bmatrix} &= \begin{bmatrix} u_1 & u_2 & \dots & u_r & u_{r+1} & \dots & u_m \end{bmatrix} \begin{bmatrix} \sigma_1 & \dots & 0 & 0 & \dots & 0\\ \dots & \dots & \dots & \dots & \dots & \dots\\ 0 & \dots & \sigma_r & 0 & \dots & 0\\ 0 & \dots & 0 & 0 & \dots & 0\\ \dots & \dots & \dots & \dots & \dots & \dots\\ 0 & \dots & 0 & 0 & \dots & 0\\ \end{bmatrix}\\ AV&= U\Sigma \end{aligned}
σ1?u1?=Av1?整合成矩阵就是A[v1??v2??…?vr??vr+1??…?vn??]AV?=[u1??u2??…?ur??ur+1??…?um??]
?σ1?…00…0?………………?0…σr?0…0?0…00…0?………………?0…00…0?
?=UΣ?
1到r是行空间/列空间的,r+1到n是零空间和左零空间的
不一次就找出两个正交矩阵U和V,消去U
A
V
=
U
Σ
A
=
U
Σ
V
?
1
=
U
Σ
V
T
A
T
A
=
(
V
Σ
T
U
T
)
U
Σ
V
?
1
A
T
A
=
V
Σ
T
Σ
V
?
1
=
V
[
σ
1
2
σ
2
2
…
]
V
T
\begin{aligned} AV &= U\Sigma\\ A &= U\Sigma V^{-1}=U\Sigma V^T\\ A^TA &= (V\Sigma^TU^T)U\Sigma V^{-1}\\ A^TA &= V\Sigma^T\Sigma V^{-1}=V \begin{bmatrix} \sigma_1^2 & &\\ & \sigma_2^2 &\\ & & \dots \end{bmatrix}V^T \end{aligned}
AVAATAATA?=UΣ=UΣV?1=UΣVT=(VΣTUT)UΣV?1=VΣTΣV?1=V
?σ12??σ22??…?
?VT?
ATA的特征向量是那些v,特征值是那些 sigma2 ,这些特征值就是奇异值
对于对称矩阵来说,V和U是一样的
eg:

反过来求AAT,特征值与ATA相同,特征向量组成U
线性变换及对应矩阵
行列式、特征值、零空间等都源自于矩阵,而矩阵的背后是线性变换
判断线性变换的两大条件:加法和数乘的不变性
平面平移不是一个线性变换
T(v)=||v||,T(-v) != -T(v)
线性变换对空间的影响体现在变换T对输入空间基向量的变换上,换句话说,只要知道T(v1), T(v2), … , T(vn),就足以确定任何v的线性变换T(v)
如果以特征向量为基,用输入基和输出基求变换矩阵,求出的变换矩阵是对角阵Lambda,对角线上都是特征值
如何确定矩阵A:给定两个基向量组v和w
- A第一列:T(v1)=a11w1 + a21w2 + … + am1wm
- A第二列:T(v2)=a12w1 + a22w2 + … + am2wm
求导是一个线性变换,所以只需要知道少量的函数的求导法则就能求出它们的线性组合的导数
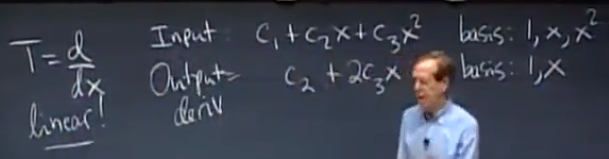
基变换和图像压缩
压缩:将图像矩阵变换成一组基能表示的矩阵
无损压缩:像素向量可以分解为一组基矩阵乘一个参数向量
像素向量
p
=
c
1
w
1
+
?
+
c
n
w
n
p
=
[
基向量组成的矩阵
]
[
c
1
…
c
n
]
c
=
W
?
1
p
\begin{aligned} 像素向量p &= c_1w_1+\dots+c_nw_n\\ p &= \begin{bmatrix} 基向量组成的矩阵 \end{bmatrix} \begin{bmatrix} c_1\\ \dots\\ c_n \end{bmatrix}\\ c&=W^{-1}p \end{aligned}
像素向量ppc?=c1?w1?+?+cn?wn?=[基向量组成的矩阵?]
?c1?…cn??
?=W?1p?
w是标准正交的,w-1=wT
使用c重构信号
x
^
=
∑
c
i
^
v
i
x
^
是压缩后的像素向量,
Σ
加和的个数是压缩后的行数(
c
的行数),如从
63
压缩到
3
,则压缩比是
21
:
1
\hat{x}=\sum{\hat{c_i}v_i}\\ \hat{x}是压缩后的像素向量,\Sigma加和的个数是压缩后的行数(c的行数),如从63压缩到3,则压缩比是21:1
x^=∑ci?^?vi?x^是压缩后的像素向量,Σ加和的个数是压缩后的行数(c的行数),如从63压缩到3,则压缩比是21:1
找到更好的基:
- 快速求c,FFT FWT
- 良好的压缩性,少量基向量就能接近信号
基变换:
[
x
]
旧基
→
[
c
]
新基
\begin{bmatrix} x \end{bmatrix}_{旧基} \rightarrow \begin{bmatrix} c \end{bmatrix}_{新基}
[x?]旧基?→[c?]新基?
x=Wc
两组基v1, … , vn和w1, … , wn同一变换得到T(v)=A 和 T(w)=B,A、B相似
B
=
M
?
1
A
M
B
=
W
?
1
A
W
B=M^{-1}AM\\ B=W^{-1}AW
B=M?1AMB=W?1AW
已知变换 T 和一组基,即知 T ( v 1 ) , T ( v 2 ) , … , T ( v n ) , v 相当于上面的 w 结果展成基的形式 T ( v n ) = a 1 n v 1 + a 2 n v 2 + ? + a n n v n A = [ a 11 … a 1 n … … a n 1 … a n n ] 压缩 x = c 1 v 1 + ? + c n v n T ( x ) = c 1 T ( v 1 ) + ? + c n T ( v n ) 已知变换T和一组基,即知T(v_1), T(v_2), \dots, T(v_n),v相当于上面的w\\ 结果展成基的形式T(v_n)=a_{1n}v_1 + a_{2n}v_2 + \dots + a_{nn}v_n\\ A=\begin{bmatrix} a_{11} & \dots & a_{1n}\\ \dots & & \dots\\ a_{n1} & \dots & a_{nn} \end{bmatrix}\\ \\ 压缩x=c_1v_1+ \dots + c_nv_n\\ T(x)=c_1T(v_1)+ \dots + c_nT(v_n) 已知变换T和一组基,即知T(v1?),T(v2?),…,T(vn?),v相当于上面的w结果展成基的形式T(vn?)=a1n?v1?+a2n?v2?+?+ann?vn?A= ?a11?…an1??……?a1n?…ann?? ?压缩x=c1?v1?+?+cn?vn?T(x)=c1?T(v1?)+?+cn?T(vn?)
当v是像素矩阵的特征向量时,此时v是完美基
T
(
v
n
)
=
λ
n
v
n
A
=
[
λ
1
λ
2
…
λ
n
]
T(v_n)=\lambda_nv_n\\ A=\begin{bmatrix} \lambda_1\\ &\lambda_2\\ &&\dots\\ &&&\lambda_n \end{bmatrix}
T(vn?)=λn?vn?A=
?λ1??λ2??…?λn??
?
取完美基很难,所以选其他的,如小波基和傅里叶基
单元检测3复习
A = A T ? 特征值是实数,存在足够的特征向量(即使特征值重复) ? 能对角化 相似矩阵特征值相同 ? B k = M ? 1 A k M A=A^T \Rightarrow 特征值是实数,存在足够的特征向量(即使特征值重复)\Rightarrow 能对角化\\ 相似矩阵特征值相同 \Rightarrow B^k=M^{-1}A^kM A=AT?特征值是实数,存在足够的特征向量(即使特征值重复)?能对角化相似矩阵特征值相同?Bk=M?1AkM

解后两项在复平面的单位圆上,不收敛也不发散
解具有周期性
无论是对称矩阵还是反对称矩阵(或正交矩阵),特征向量都是相互正交的,满足AAT=ATA
将u(t)表示成矩阵指数形式:
u
(
t
)
=
e
A
t
u
(
0
)
=
S
e
A
t
S
?
1
u
(
0
)
=
S
[
e
λ
1
t
…
e
λ
n
t
]
S
?
1
u
(
0
)
u(t)=e^{At}u(0)=Se^{At}S^{-1}u(0)=S \begin{bmatrix} e^{\lambda_1t}\\ & \dots\\ && e^{\lambda_nt} \end{bmatrix}S^{-1}u(0)
u(t)=eAtu(0)=SeAtS?1u(0)=S
?eλ1?t?…?eλn?t?
?S?1u(0)
已知A的特征值和特征向量
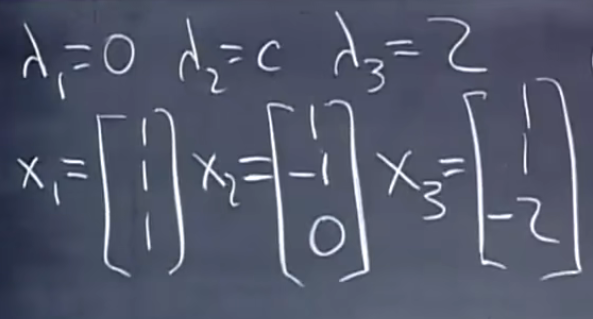
A能对角化=>任意c
A是对称矩阵=>任意实数c
A是正定矩阵=>c大于等于0
A是马尔科夫矩阵=>不可能,有大于1的特征值
A是一个投影矩阵的两倍=> P2=P投影矩阵特征值是0或1,c=0或2
正交矩阵不会改变向量长度 => Qx=lambda x两边求长度|x|=|lambda||x| => 正交矩阵特征值的绝对值为1
证明 A 是正交矩阵且是对称矩阵, 1 2 ( A + I ) 是投影矩阵 P 2 = 1 4 ( A 2 + 2 A + I ) = 1 4 ( I + 2 A + I ) = 1 2 ( A + I ) = P 1 2 ( A + I ) 的特征值 = 1 2 ( { 1 或 ? 1 } + 1 ) = 1 或 0 证明A是正交矩阵且是对称矩阵,\frac{1}{2}(A+I)是投影矩阵\\ P^2=\frac{1}{4}(A^2+2A+I)=\frac{1}{4}(I+2A+I)=\frac{1}{2}(A+I)=P\\ \frac{1}{2}(A+I)的特征值=\frac{1}{2}(\{1或-1\}+1)=1或0 证明A是正交矩阵且是对称矩阵,21?(A+I)是投影矩阵P2=41?(A2+2A+I)=41?(I+2A+I)=21?(A+I)=P21?(A+I)的特征值=21?({1或?1}+1)=1或0
左右逆和伪逆
A A ? 1 = I = A ? 1 A ? r = m = n AA^{-1}=I=A^{-1}A \Rightarrow r=m=n AA?1=I=A?1A?r=m=n
列满秩,零空间只有零解,Ax=b有0或1个解

行满秩,左零空间只有零解,Ax=b有无穷多解,n-m个自由变量

A A l e f t ? 1 = A ( A T A ) ? 1 A T = 投影到列空间上的投影矩阵 A r i g h t ? 1 A = A T ( A A T ) ? 1 A = 投影到行空间上的投影矩阵 AA^{-1}_{left}=A(A^TA)^{-1}A^T=投影到列空间上的投影矩阵\\ A^{-1}_{right}A=A^T(AA^T)^{-1}A=投影到行空间上的投影矩阵 AAleft?1?=A(ATA)?1AT=投影到列空间上的投影矩阵Aright?1?A=AT(AAT)?1A=投影到行空间上的投影矩阵
行空间中的x,经过A矩阵映射,成为列空间的Ax,另有一y,若x!=y,则A(x)!=A(y)
伪逆:列空间回到行空间 y=A+A(y)
计算伪逆的关键:找到可以快速计算伪逆的因子
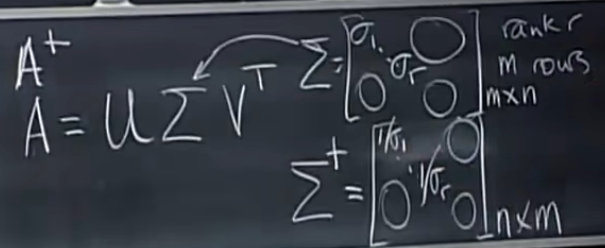
Σ
Σ
+
=
[
1
…
1
0
…
0
]
m
×
m
Σ
+
Σ
=
[
1
…
1
0
…
0
]
n
×
n
\Sigma\Sigma^+= \begin{bmatrix} 1\\ &\dots\\ &&1\\ &&&0\\ &&&&\dots\\ &&&&&0 \end{bmatrix}_{m\times m} \\ \Sigma^+\Sigma= \begin{bmatrix} 1\\ &\dots\\ &&1\\ &&&0\\ &&&&\dots\\ &&&&&0 \end{bmatrix}_{n\times n}
ΣΣ+=
?1?…?1?0?…?0?
?m×m?Σ+Σ=
?1?…?1?0?…?0?
?n×n?
A = U Σ V T A + = ( V T ) ? 1 Σ + U ? 1 = V Σ + U T \begin{aligned} A &= U\Sigma V^T\\ A^+ &= (V^T)^{-1}\Sigma^+U^{-1}=V\Sigma^+U^T \end{aligned} AA+?=UΣVT=(VT)?1Σ+U?1=VΣ+UT?
期末复习
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!