优化问题笔记(2)
3. 约束优化问题的全局解
3.1 凸优化问题
局部解成为全局解的一类重要的优化问题是所谓凸优化问题. 我们称优化问题 ( f , D ) (f,\mathcal{D}) (f,D) 是凸的/拟凸的,是指 f : D → R  ̄ f:\mathcal{D}\to\overline{\mathbb{R}} f:D→R 是凸函数/拟凸函数. 称优化问题 { min ? f 0 ( x ) s.t. f i ( x ) ≤ 0 , i = 1 , ? ? , p , h j ( x ) = 0 , j = 1 , ? ? , q , x ∈ Ω , \begin{cases}\min f_0(x)\\[1ex]\text{s.t.} f_i(x)\le0,\quad i=1,\cdots,p,\\[1ex]h_j(x)=0,\quad j=1,\cdots,q,\\[1ex]x\in\Omega,\end{cases} ? ? ??minf0?(x)s.t.fi?(x)≤0,i=1,?,p,hj?(x)=0,j=1,?,q,x∈Ω,?是凸的/拟凸的, 是指它满足如下条件:
( i ) (i) (i) f 0 f_0 f0? 是凸函数/拟凸函数;
( i i ) (ii) (ii) { f i } i = 1 p \{f_{i}\}_{i=1}^{p} {fi?}i=1p?是凸函数;
( i i i ) (iii) (iii) { h j } j = 1 q \{h_j\}_{j=1}^q {hj?}j=1q? 是仿射函数;
( i v ) (iv) (iv) Ω \Omega Ω 为 R n \mathbb{R}^n Rn 中凸集.
显然,此时可行集 D \mathcal{D} D 是凸集,( f 0 , D ) f_0,\mathcal{D}) f0?,D) 是凸问题/拟凸问题.
命题 4.3.1 (凸问题的局部解是全局解)
(1) 凸优化问题 ( f , D ) (f,\mathcal{D}) (f,D) 的局部解必为全局解.
(2) 拟凸问题 ( f , D ) (f,\mathcal{D}) (f,D) 的严格局部解必为严格全局解.
证.(1) 反证法:若 x ? x^* x? 是凸优化问题 ( f , D ) (f,\mathcal{D}) (f,D) 的局部解而不是全局解,则必存在 x ∈ D x\in\mathcal{D} x∈D, 使得 f ( x ) < f ( x ? ) f(x)<f(x^*) f(x)<f(x?).对任意的 θ ∈ ( 0 , 1 ) \theta\in(0,1) θ∈(0,1),令 x θ : = x ? + θ ( x ? x ? ) x_\theta:=x^*+\theta(x-x^*) xθ?:=x?+θ(x?x?).显然 x θ ∈ D x_\theta\in\mathcal{D} xθ?∈D,且当 θ \theta θ 充分小时, x θ x_{\theta} xθ? 充分接近 x ? x^* x?,从而 f ( x ? ) ≤ f ( x θ ) f(x^*)\leq f(x_\theta) f(x?)≤f(xθ?).于是 f ( x ? ) ≤ f ( x θ ) ≤ ( 1 ? θ ) f ( x ? ) + θ f ( x ) < ( 1 ? θ ) f ( x ? ) + θ f ( x ? ) = f ( x ? ) . \begin{aligned}f(x^*)\leq f(x_\theta)\leq(1-\theta)f(x^*)+\theta f(x)<(1-\theta)f(x^*)+\theta f(x^*)=f(x^*).\end{aligned} f(x?)≤f(xθ?)≤(1?θ)f(x?)+θf(x)<(1?θ)f(x?)+θf(x?)=f(x?).?矛盾.(上式中第二个不等号利用了凸函数的定义.)所以 x ? x^* x? 是全局解.
(2) 若 x ? x^* x? 是拟凸优化问题的 ( f , D ) (f,\mathcal{D}) (f,D) 的严格局部解而不是严格全局解,则存在 x ∈ D x\in\mathcal{D} x∈D 使得 f ( x ) ≤ f ( x ? ) f(x)\leq f(x^*) f(x)≤f(x?).沿用上面的符号,类似地,当 θ > 0 \theta>0 θ>0 充分小时,有 f ( x ? ) < f ( x θ ) ≤ max ? { f ( x ? ) , f ( x ) } = f ( x ? ) . f(x^*)<f(x_\theta)\leq\max\{f(x^*),f(x)\}=f(x^*). f(x?)<f(xθ?)≤max{f(x?),f(x)}=f(x?).矛盾. (上式中第二个不等号利用了拟凸函数的定义.)
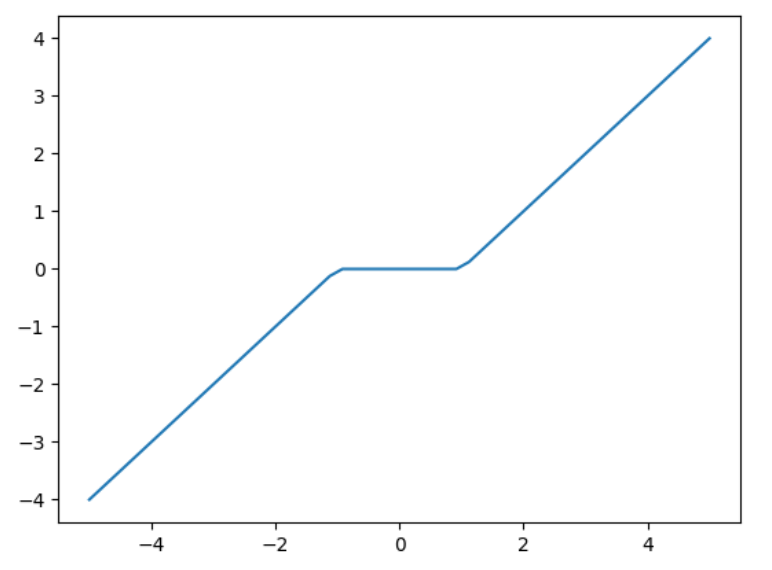
注:对于拟凸问题,非严格局部解未必是全局解. 例如函数 f ( x ) : = { x + 1 x ≤ ? 1 0 x ∈ ( ? 1 , 1 ) x ? 1 x ≥ 1 f(x):=\begin{cases}x+1&x\leq-1\\0&x\in(-1,1)\\x-1&x\geq1\end{cases} f(x):=? ? ??x+10x?1?x≤?1x∈(?1,1)x≥1?位于区间 (-1,1) 中每一点都是 ( f , R ) (f,\mathbb{R}) (f,R) 的局部最优解,但它们都不是全局最优解,如下图所示:
命题 3.1.2 (全局解与平稳点的等价性) 设凸优化问题
(
f
,
D
)
(f,\mathcal{D})
(f,D) 的目标函数
f
f
f 在
x
?
∈
D
x^*\in\mathcal{D}
x?∈D 处一阶可微,
x
?
∈
D
x^*\in\mathcal{D}
x?∈D,那么
x
?
x^*
x? 是
(
f
,
D
)
(f,\mathcal{D})
(f,D) 的一个全局最优解当且仅当
?
f
(
x
?
)
T
(
x
?
x
?
)
≥
0
,
?
x
∈
D
.
\begin{align}\nabla f(x^*)^T(x-x^*)&\ge0,\quad\forall x\in\mathcal{D}.\end{align}
?f(x?)T(x?x?)?≥0,?x∈D.??
证. 必要性.
x
?
∈
D
x^*\in\mathcal{D}
x?∈D 是一个最优解,因为
D
\mathcal{D}
D 是凸集,由优化问题笔记 (1)中的命题 1.2.1有
?
f
(
x
?
)
T
d
=
0
,
d
T
?
2
f
(
x
?
)
d
≥
0
,
?
d
∈
V
D
\nabla f(x^{*})^{T}d=0,\quad d^{T}\nabla^{2}f(x^{*})d\geq0,\quad\forall d\in V_{\mathcal{D}}
?f(x?)Td=0,dT?2f(x?)d≥0,?d∈VD?,以及由引理 1.2.2有
ξ
T
(
x
?
x
?
)
≥
0
,
?
x
∈
D
??
?
??
ξ
T
d
≥
0
,
?
d
∈
S
F
D
(
x
?
)
\xi^T(x-x^*)\ge0,\forall x\in\mathcal{D} \iff \xi^Td\ge0,\forall d\in\mathbf{SFD}(x^*)
ξT(x?x?)≥0,?x∈D?ξTd≥0,?d∈SFD(x?),于是可以推出(1)成立.
充分性. 设(1)成立. 则 ? x ∈ D \forall x\in\mathcal{D} ?x∈D,利用凸函数笔记 (1)中的命题 2.2.1,(下文直接引用,不再以链接形式给出笔记出处) f ?是凸函数当且仅当 f ( y ) ≥ f ( x ) + ? f ( x ) T ( y ? x ) , ? x , y ∈ d o m ( f ) . f\text{ 是凸函数当且仅当}f(y)\geq f(x)+\nabla f(x)^T(y-x),\quad\forall x,y\in\mathbf{dom}(f). f?是凸函数当且仅当f(y)≥f(x)+?f(x)T(y?x),?x,y∈dom(f).
于是有 f ( x ) ≥ f ( x ? ) + ? f ( x ? ) T ( x ? x ? ) ≥ f ( x ? ) . \begin{aligned}f(x)\geq f(x^*)+\nabla f(x^*)^T(x-x^*)\geq f(x^*).\end{aligned} f(x)≥f(x?)+?f(x?)T(x?x?)≥f(x?).?所以 x ? x^* x? 是 ( f , D ) (f,\mathcal{D}) (f,D) 的一个最优解.
注:当 x ? ∈ r i ( D ) x^*\in\mathbf{ri}(\mathcal{D}) x?∈ri(D) 时,由引理 1.2.2 可知 (1)等价于 ? f ( x ? ) ⊥ V D \nabla f(x^*)\perp V_\mathcal{D} ?f(x?)⊥VD?. 这意味着 x ? x^* x? 约束在 V D V_\mathrm{D} VD?上是 f f f 的一个平稳点( 满足 ? f ( x ? ) = 0 \nabla f(x^*)=0 ?f(x?)=0 的点称为 f f f 的平稳点).这一性质在优化问题的数值计算中非常重要,因为判断一个点是否为平稳点比判断其为局部极小点要容易得多.
例 3.1.1 设 A ∈ R m × n , b ∈ R m A\in\mathbb{R}^{m\times n},\quad b\in\mathbb{R}^m A∈Rm×n,b∈Rm 使得集合 { x ∈ R n ∣ A x = b } \{x\in\mathbb{R}^n|Ax=b\} {x∈Rn∣Ax=b} 非空. 又设函数 f : R n → R f:\mathbb{R}^n\to\mathbb{R} f:Rn→R 是可微的凸函数.那么, x ? ∈ R n x^*\in\mathbb{R}^n x?∈Rn 是等式约束凸优化问题 { min ? f ( x ) s . t A x = b \begin{align} \begin{cases}\min f(x)\\\mathrm{s.t}\quad Ax=b\end{cases}\end{align} {minf(x)s.tAx=b???的解当且仅当 ? f ( x ? ) ∈ r a n ( A T ) , A x ? = b . \nabla f(x^*)\in\mathbf{ran}(A^T),\quad Ax^*=b. ?f(x?)∈ran(AT),Ax?=b.证.在 例 1.2.1 中已证明该可行集 D \mathcal{D} D 满足: r i ( D ) = D \mathbf{ri}(D)=\mathcal{D} ri(D)=D 且 V D = n u l l ( A ) = r a n ( A T ) ⊥ . V_D=\mathbf{null}(A)=\mathbf{ran}(A^T)^\perp. VD?=null(A)=ran(AT)⊥. 由命题 3.1.2 可知, x ? ∈ D x^*\in\mathcal{D} x?∈D 是优化问题 (2)的一个最优解当且仅当 ? f ( x ? ) ∈ V D ⊥ \nabla f(x^*)\in V_\mathcal{D}^\perp ?f(x?)∈VD⊥?, 即 ? f ( x ? ) ∈ r a n ( A T ) . \nabla f(x^*)\in\mathbf{ran}(A^T). ?f(x?)∈ran(AT).
3.2 二次优化问题
当目标函数和约束函数都是二次 (不超过二次) 函数时, L ( x , λ , μ ) L(x, λ, μ) L(x,λ,μ) 关于 x x x也是二次函数,因而其 Taylor 展开式展开到二次项时余项为 0. 此时, 有如下全局解的充分条件.
命题 3.2.1 (二次优化问题全局解的充分条件) 对于不含约束集的约束优化问题 { min ? f 0 ( x ) s . t f i ( x ) ≤ 0 , i = 1 , ? ? , p , h j ( x ) = 0 , j = 1 , ? ? , q . \begin{cases}\min f_0(x)\\\mathrm{s.t}\quad f_i(x)\leq0,\quad i=1,\cdots,p,\\h_j(x)=0,\quad j=1,\cdots,q.&\end{cases} ? ? ??minf0?(x)s.tfi?(x)≤0,i=1,?,p,hj?(x)=0,j=1,?,q.??, 设 { f i } i = 0 p , { h j } j = 1 q \{f_i\}_{i=0}^p,\{h_j\}_{j=1}^q {fi?}i=0p?,{hj?}j=1q? 均为二次函数, x ? ∈ R n x^*\in\mathbb{R}^n x?∈Rn,存在 λ ? ∈ R p , μ ? ∈ R q \lambda^*\in\mathbb{R}^p,\mu^*\in\mathbb{R}^q λ?∈Rp,μ?∈Rq,满足 K K T KKT KKT 条件 { x ? ∈ D ; λ i ? ≥ 0 , i = 1 , ? ? , p ; λ i ? f i ( x ? ) = 0 , i = 1 , ? ? , p ; ? x L ( x ? , λ ? , μ ? ) = 0. \begin{cases}x^*\in\mathcal{D};\\\lambda_i^*\geq0,\quad i=1,\cdots,p;\\\lambda_i^*f_i(x^*)=0,\quad i=1,\cdots,p;\\\nabla_xL(x^*,\lambda^*,\mu^*)=0.\end{cases} ? ? ??x?∈D;λi??≥0,i=1,?,p;λi??fi?(x?)=0,i=1,?,p;?x?L(x?,λ?,μ?)=0.?,且有下式: ( x ? x ? ) T ? x 2 L ( x ? , λ ? , μ ? ) ( x ? x ? ) ≥ 0 , ? x ∈ D \begin{align} (x-x^*)^T\nabla_x^2L(x^*,\lambda^*,\mu^*)(x-x^*)\geq0,\quad\forall x\in\mathcal{D}\end{align} (x?x?)T?x2?L(x?,λ?,μ?)(x?x?)≥0,?x∈D??则 x ? x^* x? 是一个全局最优解.
证.对任意的
x
∈
D
x\in\mathcal{D}
x∈D,记
d
:
=
x
?
x
?
d:=x-x^*
d:=x?x?,那么
f
0
(
x
)
≥
L
(
x
,
λ
?
,
μ
?
)
=
L
(
x
?
,
λ
?
,
μ
?
)
+
d
T
?
x
L
(
x
?
,
λ
?
,
μ
?
)
+
1
2
d
T
?
x
2
L
(
x
?
,
λ
?
,
μ
?
)
T
d
≥
L
(
x
?
,
λ
?
,
μ
?
)
=
f
0
(
x
?
)
.
\begin{aligned} \begin{aligned}f_0(x)\geq L(x,\lambda^*,\mu^*)\end{aligned}& =L(x^*,\lambda^*,\mu^*)+d^T\nabla_xL(x^*,\lambda^*,\mu^*)+\frac12d^T\nabla_x^2L(x^*,\lambda^*,\mu^*)^Td \\ &\geq L(x^{*},\lambda^{*},\mu^{*})=f_{0}(x^{*}). \end{aligned}
f0?(x)≥L(x,λ?,μ?)??=L(x?,λ?,μ?)+dT?x?L(x?,λ?,μ?)+21?dT?x2?L(x?,λ?,μ?)Td≥L(x?,λ?,μ?)=f0?(x?).? 所以
x
?
x^*
x? 是一个全局最优解.
注:当 x ? x^* x? 是一个正则点时,根据 定义 2.1.3 有 T ( x ? ) ∩ ? B ( 0 , 1 ) ? L F D ( x ? ) = S F D ( x ? )  ̄ \mathcal{T}(x^*)\cap\partial B(0,1)\subset\mathbf{LFD}(x^*)=\mathbf{SFD}(\overline{x^*)} T(x?)∩?B(0,1)?LFD(x?)=SFD(x?)?.根据 引理 1.2.2 可知,本命题的条件(3) 比局部解的二阶必要条件 d T ? x 2 L ( x ? , λ ? , μ ? ) d ≥ 0 , ? d ∈ T ( x ? ) d^T\nabla_x^2L(x^*,\lambda^*,\mu^*)d\geq0,\quad\forall d\in\mathcal{T}(x^*) dT?x2?L(x?,λ?,μ?)d≥0,?d∈T(x?) 要强.
3.3 无约束二次优化问题
命题 3.3.1 (二次函数之最优解的条件) 设 f ( x ) : = 1 2 x T A x + b T x f(x):=\frac12x^TAx+b^Tx f(x):=21?xTAx+bTx, 其中 A A A 是 n n n 阶实对称矩阵, x ? ∈ R n x^*\in\mathbb{R}^n x?∈Rn.那么,对于无约束优化问题 ( f , R n ) (f,\mathbb{R}^n) (f,Rn),即问题 { min ? f 0 ( x ) s . t f i ( x ) ≤ 0 , i = 1 , ? ? , p , h j ( x ) = 0 , j = 1 , ? ? , q . \begin{cases}\min f_0(x)\\\mathrm{s.t}\quad f_i(x)\leq0,\quad i=1,\cdots,p,\\h_j(x)=0,\quad j=1,\cdots,q.&\end{cases} ? ? ??minf0?(x)s.tfi?(x)≤0,i=1,?,p,hj?(x)=0,j=1,?,q.??,如下三条相互是等价的:
( 3.3.1.1 ) ? x ? (3.3.1.1)\:x^* (3.3.1.1)x? 是 f f f 的一个全局极小点;
( 3.3.1.2 ) ? x ? (3.3.1.2)\:x^* (3.3.1.2)x? 是 f f f 的一个局部极小点;
( 3.3.1.3 ) A (3.3.1.3)A (3.3.1.3)A 是半正定矩阵且 A x ? + b = 0. Ax^*+b=0. Ax?+b=0.
证.根据全局最小点和局部极小点的定义可以知道, (3.3.1.1) 蕴含 (3.3.1.2). 对 f f f 计算可得 ? f ( x ? ) = A x ? + b , ? 2 f ( x ? ) = A . \begin{align} \begin{aligned}\nabla f(x^*)=Ax^*+b,\quad\nabla^2f(x^*)=A.\end{aligned}\end{align} ?f(x?)=Ax?+b,?2f(x?)=A.???因此,若 (3.3.1.2) 成立,那么,由 必要性命题 1.2.1:若 f f f 在 x ? x^* x? 处二阶连续可微,且 x ? ∈ r i ( D ) x^*\in\mathbf{ri}(\mathcal{D}) x?∈ri(D),则 ? f ( x ? ) T d = 0 , d T ? 2 f ( x ? ) d ≥ 0 , ? d ∈ V D . \nabla f(x^{*})^{T}d=0,\quad d^{T}\nabla^{2}f(x^{*})d\geq0,\forall d\in V_{\mathcal{D}}. ?f(x?)Td=0,dT?2f(x?)d≥0,?d∈VD?.即知 (3.3.1.3) 成立.
设 (3.3.1.3)成立. 利用(4)可知 ? f ( x ? ) = 0 \nabla f(x^*)=0 ?f(x?)=0,且 ? 2 f ( x ? ) \nabla^2f(x^*) ?2f(x?) 半正定. 于是, ? x ∈ R n \forall x\in\mathbb{R}^n ?x∈Rn,做Taylor 展开,有 f ( x ) = f ( x ? ) + 1 2 ( x ? x ? ) T A ( x ? x ? ) ≥ f ( x ? ) . f(x)=f(x^*)+\frac12(x-x^*)^TA(x-x^*)\geq f(x^*). f(x)=f(x?)+21?(x?x?)TA(x?x?)≥f(x?).所以 x ? x^* x? 是 f f f 在 R n \mathbb{R}^n Rn 上的最小点. 即(3.3.1.1) 成立.
注:二次函数 f ( x ) : = 1 2 x T A x + b T x f(x):=\frac12x^TAx+b^Tx f(x):=21?xTAx+bTx 未必总存在极小值点. 事实上,当 A A A 不是半正定矩阵时,或者 A A A半正定但 A x + b = 0 Ax+ b= 0 Ax+b=0 无解时, f ( x ) f(x) f(x) 就不存在极小值点. 此时, inf ? x ∈ R n f ( x ) = ? ∞ \inf_{x\in\mathbb{R}^n}f(x)=-\infty infx∈Rn?f(x)=?∞.例如,对于 A = [ 0 0 0 1 ] , b : = [ b 1 0 ] , c = 0 , A=\begin{bmatrix}0&0\\0&1\end{bmatrix},\quad b:=\begin{bmatrix}b_1\\0\end{bmatrix},\quad c=0, A=[00?01?],b:=[b1?0?],c=0,有 f ( x ) = 1 2 x 2 2 + b 1 x 1 , ? x : = ( x 1 , x 2 ) T ∈ R 2 f(x)=\frac12x_2^2+b_1x_1,\:x:=(x_1,x_2)^T\in\mathbb{R}^2 f(x)=21?x22?+b1?x1?,x:=(x1?,x2?)T∈R2.当 b 1 ≠ 0 b_1\neq0 b1?=0 时, f ( x ) f(x) f(x) 不存在最小值点.
推论 3.3.1 (二次函数之全局最优解存在的条件) 设 A A A 是 n n n 阶实对称矩阵,那么,二次函数 f ( x ) : = 1 2 x T A x + b T x f(x):=\frac12x^TAx+b^Tx f(x):=21?xTAx+bTx 在 R n \mathbb{R}^n Rn 上有最小值点当且仅当 f ( x ) f(x) f(x) 在 R n \mathbb{R}^n Rn 上有下界.
证.将
A
A
A做特征分解
A
=
U
Λ
U
T
A=U\Lambda U^T
A=UΛUT ,其中
U
U
U 是一个
n
n
n 阶正交矩阵,
Λ
=
d
i
a
g
(
λ
1
,
.
.
.
,
λ
n
)
\Lambda=\mathbf{diag}(\lambda_1,...,\lambda_n)
Λ=diag(λ1?,...,λn?), 其中
λ
1
≥
.
.
.
≥
λ
n
\lambda_1\geq...\geq\lambda_n
λ1?≥...≥λn? 是
A
A
A 的全部特征值. 令
y
:
=
U
T
x
,
?
q
:
=
U
T
b
y:=U^Tx,~q:=U^Tb
y:=UTx,?q:=UTb, 那么
f
(
x
)
=
1
2
y
T
Λ
y
+
q
T
y
=
1
2
∑
i
=
1
n
(
λ
i
y
i
2
+
2
q
i
y
i
)
.
f(x)=\frac12y^T\Lambda y+q^Ty=\frac12\sum_{i=1}^n(\lambda_iy_i^2+2q_iy_i).
f(x)=21?yTΛy+qTy=21?i=1∑n?(λi?yi2?+2qi?yi?).所以
f
(
x
)
f(x)
f(x) 在
R
n
\mathbb{R}^n
Rn 上有下界当且仅当对每一个
1
≤
i
≤
n
1\leq i\leq n
1≤i≤n, 单变量函数
g
i
(
y
)
:
=
λ
i
y
2
+
2
q
i
y
g_i(y):=\lambda_iy^2+2q_iy
gi?(y):=λi?y2+2qi?y在 R 上有下界.即
λ
i
≥
0
\lambda_i\geq0
λi?≥0 且
λ
i
=
0
\lambda_i=0
λi?=0 时,有
q
i
=
0
q_i=0
qi?=0. 此时,当
y
i
:
=
{
?
q
i
λ
i
λ
i
>
0
,
任意值
λ
i
=
0
,
i
=
1
,
.
.
.
,
n
.
y_i:=\begin{cases}-\frac{q_i}{\lambda_i}&\lambda_i>0,\\\text{任意值}&\lambda_i=0,&\end{cases}\quad i=1,...,n.
yi?:={?λi?qi??任意值?λi?>0,λi?=0,??i=1,...,n.时,
x
=
U
y
x= Uy
x=Uy是
f
(
x
)
f(x)
f(x) 在
R
n
\mathbb{R} ^n
Rn 上的一个最小值点.
例 3.3.1 (最小二乘问题 (LSP: Least Square Problem)) 给定矩阵 A ∈ R m × n A\in\mathbb{R}^{m\times n} A∈Rm×n 和向量 b ∈ R m b\in\mathbb{R}^m b∈Rm, 如下无约束优化问题 min ? ∥ A x ? b ∥ 2 2 \begin{align} \min\|Ax-b\|_2^2\end{align} min∥Ax?b∥22???称为最小二乘问题. x ? x^* x? 是其最优解当且仅当 ( A T A ) x ? = A T b (A^TA)x^*=A^Tb (ATA)x?=ATb. 该问题的解一定存在且构成一个 n ? r n-r n?r 维仿射空间,其中 r : = r a n k ( A ) r: = \mathbf{rank}( A) r:=rank(A)
证.计算可得 ∥ A x ? b ∥ 2 2 = x T ( A T A ) x ? 2 b T A x + ∥ b ∥ 2 2 , \|Ax-b\|_2^2=x^T(A^TA)x-2b^TAx+\|b\|_2^2, ∥Ax?b∥22?=xT(ATA)x?2bTAx+∥b∥22?,根据线性代数的内容,假设 A A A 的列向量分别是 α 1 , ? ? , α n \alpha_1,\cdots,\alpha_n α1?,?,αn?,那么有: ∣ A X 0 ? b ∣ ?最小 ? 对于任意的? X ?都有? ∣ A X 0 ? b ∣ ≤ ∣ A X ? b ∣ ? A X 0 ? b ⊥ U ?其中? U = { A X ∣ X ∈ R n } = L ( α 1 , ? ? , α n ) ? A X 0 ? b ⊥ α i ( i = 1 , 2 , ? ? , n ) ? α i ′ ( A X 0 ? b ) = 0 ( i = 1 , 2 , ? ? , n ) ? ( α 1 ′ ? α n ′ ) ( A X 0 ? b ) = 0 ? A ′ ( A X 0 ? b ) = 0 ? A ′ A X 0 = A ′ b . \begin{aligned} |AX_{0}-b|\text{ 最小}& \Longleftrightarrow\text{对于任意的 }X\text{ 都有 }|AX_0-b|\leq|AX-b| \\ &\Longleftrightarrow AX_0-b\perp U\text{ 其中 }U=\{AX|X\in\mathbb{R}^n\}=L(\alpha_1,\cdots,\alpha_n) \\ &\Longleftrightarrow AX_0-b\perp\alpha_i(i=1,2,\cdots,n) \\ &\Longleftrightarrow\alpha_i'(AX_0-b)=0(i=1,2,\cdots,n) \\ &\left.\Longleftrightarrow\left(\begin{array}{c}\alpha_1'\\\vdots\\\alpha_n'\end{array}\right.\right)(AX_0-b)=0 \\ &\Longleftrightarrow A^{\prime}(AX_{0}-b)=0 \\ &\Longleftrightarrow A^{\prime}AX_{0}=A^{\prime}b. \end{aligned} ∣AX0??b∣?最小??对于任意的?X?都有?∣AX0??b∣≤∣AX?b∣?AX0??b⊥U?其中?U={AX∣X∈Rn}=L(α1?,?,αn?)?AX0??b⊥αi?(i=1,2,?,n)?αi′?(AX0??b)=0(i=1,2,?,n)? ?α1′??αn′?? ?(AX0??b)=0?A′(AX0??b)=0?A′AX0?=A′b.?记 r : = r a n k ( A ) r: = \mathbf{rank}( A) r:=rank(A),即 r r r表示矩阵的秩
一方面 r ( A ′ A , A ′ b ) = r ( A ′ ( A , b ) ) ≤ r ( A ′ ) = r ( A ) . r(A^{\prime}A,A^{\prime}b)=r(A^{\prime}(A,b))\leq r(A^{\prime})=r(A). r(A′A,A′b)=r(A′(A,b))≤r(A′)=r(A).另一方面 r ( A ′ A , A ′ b ) ≥ r ( A ′ A ) = r ( A ) , r(A^{\prime}A,A^{\prime}b)\geq r(A^{\prime}A)=r(A), r(A′A,A′b)≥r(A′A)=r(A),这就说明 r ( A ′ A , A ′ b ) = r ( A ) = r ( A ′ A ) . r(A^{\prime}A,A^{\prime}b)=r(A)=r(A^{\prime}A). r(A′A,A′b)=r(A)=r(A′A).
所以线性方程组 ( A T A ) x ? = ? A T b (A^TA)x\:=\:A^Tb (ATA)x=ATb 有解,且其解就是上述最小二乘问题的解.
根据上面的推导可以知道,该线性方程组的增广矩阵 ( A T A , A T b ) = A T ( A , b ) (A^TA,A^Tb)=A^T(A,b) (ATA,ATb)=AT(A,b) 的秩就等于 r a n k ( A T ) = r = r a n k ( A T A ) , \mathbf{rank}(A^T)=r=\mathbf{rank}(A^TA), rank(AT)=r=rank(ATA), 所以该线性方程组有解,其有 n ? r n-r n?r 个基向量,且解空间构成一个 n ? r n-r n?r 维仿射空间.
3.4 一个典型的二次等式约束二次优化问题
给定 n n n阶对称矩阵 A , B A,B A,B,考虑如下的优化问题: { min ? x T A x s . t ? x T x = 1 , x T B x = 1. \begin{align}\begin{cases}\min x^TAx\\\mathrm{s.t~}x^Tx=1,\\x^TBx=1.&\end{cases}\end{align} ? ? ??minxTAxs.t?xTx=1,xTBx=1.????记 D : = { x ∈ R n ∣ x T x = 1 , x T B x = 1 } \mathcal{D}:=\{x\in\mathbb{R}^n|x^Tx=1,x^TBx=1\} D:={x∈Rn∣xTx=1,xTBx=1},当 D \mathcal{D} D 非空时, 根据函数的连续性可知该优化问题的全局最优解是存在的.
若 x ? ∈ D x^? ∈ \mathcal{D} x?∈D 是问题(6)的全局解, 且 { x ? , B x ? } \left \{ x^?, Bx^? \right \} {x?,Bx?} 线性无关, 根据局部解的二阶必要条件 (命题 2.2.5),存在 α ? , β ? ∈ R \alpha^*,\beta^*\in\mathbb{R} α?,β?∈R, 使得 H x ? = 0 , d T H d ≥ 0 , ? d ∈ T ( x ? ) , \begin{align} Hx^*=0,\quad d^THd\geq0,\quad\forall d\in\mathcal{T}(x^*),\end{align} Hx?=0,dTHd≥0,?d∈T(x?),??其中, T ( x ? ) : = ( s p a n { x ? , B x ? } ) ⊥ \mathcal{T}(x^*):=\left(\mathbf{span}\{x^*,Bx^*\}\right)^\perp T(x?):=(span{x?,Bx?})⊥ 是问题(6) 的约束条件的切空间,而根据命题 3.2.1当 H x ? = 0 , d T H d ≥ 0 , ? d ∈ D ? x ? , \begin{align} Hx^*=0,\quad d^THd\geq0,\quad\forall d\in\mathcal{D}-x^*,\end{align} Hx?=0,dTHd≥0,?d∈D?x?,??时, x ? x^* x? 是问题(6)全局解.
下面命题则可以说明必要条件可以加强为 H x ? = 0 , ? H ? 0. Hx^*=0,~H\succeq0. Hx?=0,?H?0.
命题 3.4.1 (Bar-on and Grasse) 设 x ? ∈ D x^*\in\mathcal{D} x?∈D,且使得 { x ? , R x ? } \{x^*,Rx^*\} {x?,Rx?} 线性无关,则 x ? x^* x? 是问题(6)的全局解当且仅当存在 α ? , β ? ∈ R \alpha^*,\beta^*\in\mathbb{R} α?,β?∈R, 使得(8)所定义的 H H H 满足: H x ? = 0 , H ? 0. \begin{align} Hx^*=0,\quad H\succeq0.\end{align} Hx?=0,H?0.??
Reference
包括但不限于以下内容:
(1)Stephen Boyd, Stephen P Boyd, and Lieven Vandenberghe. Convex
optimization. Cambridge university press, 2004.
(2) JR Bar-On and KA Grasse. Global optimization of a quadratic functional with quadratic equality constraints. Journal of Optimization Theory and Applications, 82(2):379–386, 1994.
(3) JR Bar-On and KA Grasse. Global optimization of a quadratic functional with quadratic equality constraints, part 2. Journal of Optimization Theory and Applications, 93(3):547–556, 1997.
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!