电磁波散射

2023-12-31 21:37:18

一、电磁散射概念和雷达截面（RCS）

1. 电磁散射概念

入射场E^i和H^i

散射场E^s和H^s

总场E^{'}和H^{'}

物质外部：

E^{'} = E^i + E^s

H^{'} = H^i + H^s

2. 雷达截面

（1）截获功率

在距离散射体距离r趋向于无限远处某观测点被观测到的散射场功率流密度S_s乘以球面积4\pi r^2

P_c = \lim_{s \rightarrow \infty} S_s 4\pi r^2

（2）雷达截面

散射体从入射波中所截获的功率P_c与入射功率流密度S_i成正比，这个比例系数定义为雷达截面\sigma

P_c = \sigma S_i

\sigma = \lim_{r \rightarrow \infty} 4\pi r^2 \frac{S_s}{S_i}

一般认为，入射波的波源和散射波的观察点距离散射体都很远，所以

S_i = \frac{|E^i|^2}{2Z_0}

S_s = \frac{|E^s|^2}{2Z_0}

\sigma = \lim_{r \rightarrow \infty} 4\pi r^2 \frac{|E^s|^2}{|E^i|^2}

对于三维和二维散射体，散射远场存在以下形式

E|_{r \rightarrow \infty} = \frac{\exp{(-jk_0r)}}{r} F(\theta, \phi)

E|_{r \rightarrow \infty} = \frac{\exp{(-jk_0 \rho)}}{\rho} f(\phi)

因此，散射截面与波的入射方向和散射方向有关。

二、雷达方程

1. 传输方程

（1）发射信号功率流密度

P_t：发射机功率

\Gamma_t：发射天线输入端的反射率

G_t：发射天线增益

计算发射天线产生的功率流密度为：

S_t = \frac{P_t}{4 \pi R^2} \left( 1-|\Gamma_t|^2 \right ) G_t (\theta_t, \phi_t)

（2）接收天线有效面积

天线的最大有效面积

A_{em} = \frac{\lambda^2}{4\pi} D_0

有效面积

A_e = A_{em} \eta_{cd} |\hat{\rho_w} \cdot \hat{\rho_a}|^2 \left( 1-|\Gamma|^2 \right) \\ = \frac{\lambda^2}{4\pi} D_0 \eta_{cd} |\hat{\rho_w} \cdot \hat{\rho_a}|^2 \left( 1-|\Gamma|^2 \right) \\ = \frac{\lambda^2}{4\pi} G_0 |\hat{\rho_w} \cdot \hat{\rho_a}|^2 \left( 1-|\Gamma|^2 \right) \\ = \frac{\lambda^2}{4\pi} \left( 1-|\Gamma|^2 \right) G_0 |\hat{\rho_w} \cdot \hat{\rho_a}|^2

接收天线的有效面积：

A_r = \frac{\lambda^2}{4\pi} (1-|\Gamma_r|^2) G_r(\theta_r, \phi_r) |\hat{\rho_t} \cdot \hat{\rho_r}|^2

（3）接收到的功率

P_r = A_r S_t

(4) 接收功率与入射功率之比

\frac{P_r}{P_t} = \left( 1-|\Gamma_t|^2 \right ) \left( 1-|\Gamma_r|^2 \right ) \left( \frac{\lambda}{4\pi R} \right )^2 G_t(\theta_t, \phi_t) G_r(\theta_r, \phi_r) |\hat{\rho_t} \cdot \hat{\rho_r}|^2

最大值：\left( \frac{\lambda}{4\pi R} \right )^2 D_{0t} D_{0r}

2. 距离方程

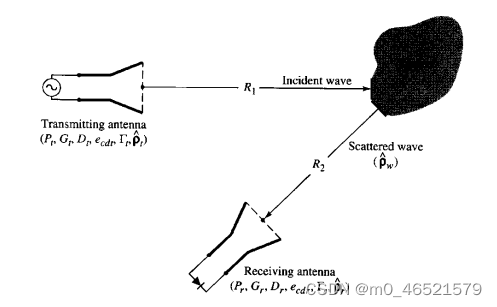
设散射体散射截面为\sigma，散射体截获的入射波功率为

P_c = \sigma S_t = \sigma \frac{P_t}{4\pi R_1^2} \left( 1 - |\Gamma_t|^2 \right ) G_t(\theta_t, \phi_t)

截获功率被散射体各向均匀散射，接收天线处的功率流密度

S_s = \frac{P_c}{4\pi R_2^2}

接收天线的有效面积

A_r = \frac{\lambda^2}{4\pi} (1-|\Gamma_r|^2) G_r(\theta_r, \phi_r) |\hat{\rho_s} \cdot \hat{\rho_r}|^2

接收功率

P_r = S_s A_r

接收功率与入射功率之比

\frac{P_r}{P_t} = \sigma (1-|\Gamma_t|^2) (1-|\Gamma_r|^2) \left( \frac{\lambda}{4\pi R_1 R_2} \right )^2 \frac{G_t(\theta_t, \phi_t) G_r(\theta_r, \phi_r)}{4\pi} |\hat{\rho_s} \cdot \hat{\rho_r}|^2

对于后向散射，如果发射天线和接收天线使用同一个天线，没有极化损失和匹配损失，则接收到的功率为

P_{0r} = P_t \sigma \left( \frac{\lambda}{4 \pi R^2} \right )^2 \frac{G_0^2}{4\pi} \\= \frac{P_t\sigma A_{0r} G_0}{(4\pi)^2 R^4}

3. 雷达搜索方程

4. 雷达跟踪方程

文章来源:https://blog.csdn.net/m0_46521579/article/details/135301802
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。