优化算法2D可视化

2023-12-23 19:39:35

简要介绍图中的优化算法，编程实现并2D可视化

1. 被优化函数?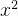x^{2}

SGD算法：

SGD算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。（重点：每次迭代使用一组样本。）
为什么叫随机梯度下降算法呢？这里的随机是指每次迭代过程中，样本都要被随机打乱，这个也很容易理解，打乱是有效减小样本之间造成的参数更新抵消问题。这种随机性使得算法更具鲁棒性，能够避免陷入局部极小值，并且训练速度也会更快。

将被优化函数实现为OptimizedFunction算子，其forward方法是Sphere函数的前向计算，backward方法则计算被优化函数对xx的偏导
import torch
class OptimizedFunction(Op):
    def __init__(self, w):
        super(OptimizedFunction, self).__init__()
        self.w = w
        self.params = {'x': 0}
        self.grads = {'x': 0}

    def forward(self, x):
        self.params['x'] = x
        return torch.matmul(self.w.T, torch.tensor(torch.square(self.params['x']), dtype=torch.float32))

    def backward(self):
        self.grads['x'] = 2 * torch.multiply(self.w.T, self.params['x'])
训练函数?定义一个简易的训练函数，记录梯度下降过程中每轮的参数x和损失
def train_f(model, optimizer, x_init, epoch):
    x = x_init
    all_x = []
    losses = []
    for i in range(epoch):
        all_x.append(copy.copy(x.numpy()))
        loss = model(x)
        losses.append(loss)
        model.backward()
        optimizer.step()
        x = model.params['x']
    return torch.tensor(all_x), losses
可视化函数?定义一个Visualization类，用于绘制x的更新轨迹
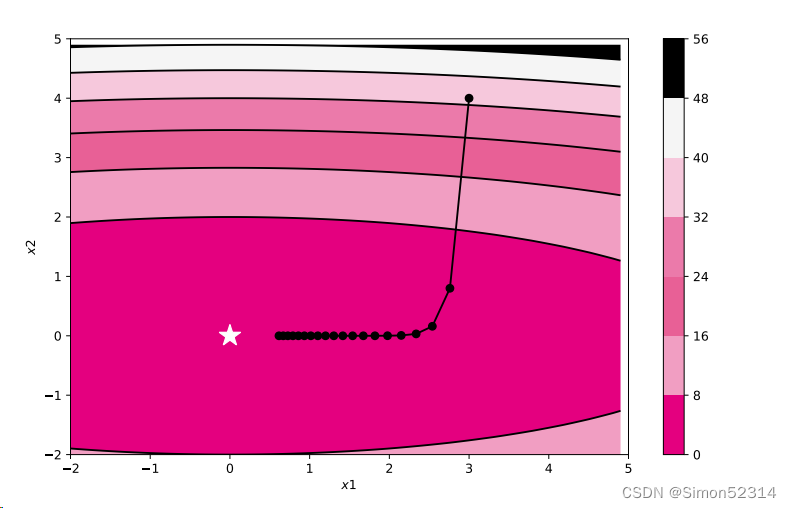
class Visualization(object):
    def __init__(self):
        """
        初始化可视化类
        """
        # 只画出参数x1和x2在区间[-5, 5]的曲线部分
        x1 = np.arange(-5, 5, 0.1)
        x2 = np.arange(-5, 5, 0.1)
        x1, x2 = np.meshgrid(x1, x2)
        self.init_x = torch.tensor([x1, x2])

    def plot_2d(self, model, x, fig_name):
        """
        可视化参数更新轨迹
        """
        fig, ax = plt.subplots(figsize=(10, 6))
        cp = ax.contourf(self.init_x[0], self.init_x[1], model(self.init_x.transpose(0, 1)),
                         colors=['#e4007f', '#f19ec2', '#e86096', '#eb7aaa', '#f6c8dc', '#f5f5f5', '#000000'])
        c = ax.contour(self.init_x[0], self.init_x[1], model(self.init_x.transpose(0, 1)), colors='black')
        cbar = fig.colorbar(cp)
        ax.plot(x[:, 0], x[:, 1], '-o', color='#000000')
        ax.plot(0, 'r*', markersize=18, color='#fefefe')

        ax.set_xlabel('$x1$')
        ax.set_ylabel('$x2$')

        ax.set_xlim((-2, 5))
        ax.set_ylim((-2, 5))
        plt.savefig(fig_name)
定义train_and_plot_f函数，调用train_f和Visualization，训练模型并可视化参数更新轨迹
def train_and_plot_f(model, optimizer, epoch, fig_name):
    """
    训练模型并可视化参数更新轨迹
    """
    # 设置x的初始值
    x_init = torch.tensor([3, 4], dtype=torch.float32)
    print('x1 initiate: {}, x2 initiate: {}'.format(x_init[0].numpy(), x_init[1].numpy()))
    x, losses = train_f(model, optimizer, x_init, epoch)
    print(x)
    losses = np.array(losses)

    # 展示x1、x2的更新轨迹
    vis = Visualization()
    vis.plot_2d(model, x, fig_name)
模型训练与可视化?指定Sphere函数中ww的值，实例化被优化函数，通过小批量梯度下降法更新参数，并可视化x的更新轨迹。
from nndl4.opitimizer import SimpleBatchGD
# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = SimpleBatchGD(init_lr=0.2, model=model)
train_and_plot_f(model, opt, epoch=20, fig_name='opti-vis-para.pdf')

输出图中不同颜色代表f(x_{1},x_{2})的值，具体数值可以参考图右侧的对应表，比如深粉色区域代表f(x_{1},x_{2})在0～8之间，不同颜色间黑色的曲线是等值线，代表落在该线上的点对应的f(x_{1},x_{2})的值都相同。

Adagrad算法：

小批量随机梯度按元素平方的累加变量S_{t}?出现在学习率的分母项中。因此，如果目标函数有关自变量中某个元素的偏导数一直都较大，那么该元素的学习率将下降较快；反之，如果目标函数有关自变量中某个元素的偏导数一直都较小，那么该元素的学习率将下降较慢。然而，由于S_{t}一直在累加按元素平方的梯度，自变量中每个元素的学习率在迭代过程中一直在降低（或不变）。所以，当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。

构建优化器?定义Adagrad类，继承Optimizer类。定义step函数调用adagrad进行参数更新
class Adagrad(Optimizer):
    def __init__(self, init_lr, model, epsilon):
        super(Adagrad, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.epsilon = epsilon

    def adagrad(self, x, gradient_x, G, init_lr):
        G += gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G

    def step(self):
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)
2D可视化实验?使用被优化函数展示Adagrad算法的参数更新轨迹。
# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = Adagrad(init_lr=0.5, model=model, epsilon=1e-7)
train_and_plot_f(model, opt, epoch=50, fig_name='opti-vis-para2.pdf')

AdaGrad算法在前几个回合更新时参数更新幅度较大，随着回合数增加，学习率逐渐缩小，参数更新幅度逐渐缩小。在AdaGrad算法中，如果某个参数的偏导数累积比较大，其学习率相对较小。相反，如果其偏导数累积较小，其学习率相对较大。但整体随着迭代次数的增加，学习率逐渐缩小。该算法的缺点是在经过一定次数的迭代依然没有找到最优点时，由于这时的学习率已经非常小，很难再继续找到最优点。

?RMSprop算法：

构建优化器?定义RMSprop类，继承Optimizer类。定义step函数调用rmsprop更新参数
class RMSprop(Optimizer):
    def __init__(self, init_lr, model, beta, epsilon):
        """
        RMSprop优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - beta：衰减率
            - epsilon：保持数值稳定性而设置的常数
        """
        super(RMSprop, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.beta = beta
        self.epsilon = epsilon
 
    def rmsprop(self, x, gradient_x, G, init_lr):
        """
        rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
        """
        G = self.beta * G + (1 - self.beta) * gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)
?2D可视化实验?使用被优化函数展示RMSprop算法的参数更新轨迹。
# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = RMSprop(init_lr=0.1, model=model, beta=0.9, epsilon=1e-7)
train_and_plot_f(model, opt, epoch=50, fig_name='opti-vis-para3.pdf')

从图像上来看，收敛速度越来越快，因为每次迭代中维护一个指数加权平均值，用于调整每个参数的学习率。如果某个参数的梯度较大，则RMSprop算法会自动减小它的学习率，以避免发生过冲；如果梯度较小，则会增加学习率，使得模型能够更快地收敛。这种自适应调整学习率的方式使得RMSprop算法在处理不同数据集和不同问题时更具灵活性，总之就是RMSprop算法的收敛速度越来越快，是因为它能够自适应地调整每个参数的学习率，以适应不同阶段和不同问题的需要。

Momentum算法：

构建优化器?定义Momentum类，继承Optimizer类
class Momentum(Optimizer):
    def __init__(self, init_lr, model, rho):
        """
        Momentum优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - rho：动量因子
        """
        super(Momentum, self).__init__(init_lr=init_lr, model=model)
        self.delta_x = {}
        for key in self.model.params.keys():
            self.delta_x[key] = 0
        self.rho = rho
 
    def momentum(self, x, gradient_x, delta_x, init_lr):
        """
        momentum算法更新参数，delta_x为梯度的加权移动平均
        """
        delta_x = self.rho * delta_x - init_lr * gradient_x
        x += delta_x
        return x, delta_x
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
                                                                      self.model.grads[key],
                                                                      self.delta_x[key],
                                                                      self.init_lr)
2D可视化实验?使用被优化函数展示Momentum算法的参数更新轨迹。
                                                                     self.init_lr)
# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = Momentum(init_lr=0.01, model=model, rho=0.9)
train_and_plot_f(model, opt, epoch=50, fig_name='opti-vis-para4.pdf')

从输出结果看，在模型训练初期，梯度方向比较一致，参数更新幅度逐渐增大，起加速作用；在迭代后期，参数更新幅度减小，在收敛值附近振荡。

Adam算法?

可以看作动量法和RMSprop算法的结合，不但使用动量作为参数更新方向，而且可以自适应调整学习率。

Adam算法一方面计算梯度平方g_{t}^{2}的加权移动平均（和RMSprop算法类似），另一方面计算梯度g_{t}的加权移动平均（和动量法类似）。

M_{t}=\beta _{1}M_{t-1}+(1-\beta_{1})g_{t}

G_{t}=\beta _{2}G_{t-1}+(1-\beta_{2})g_{t} \odot g_{t}

其中和分别为两个移动平均的衰减率，通常取值为\beta _1=0.9,\beta _2=0.99。我们可以把M_t和G_t分别看作梯度的均值(一阶矩)和未减去均值的方差(二阶矩)。

假设M_0=0,G_0=0，那么在迭代初期和的值会比真实的均值和方差要小。特别是当M_0=0,G_0=0都接近于1时，偏差会很大。因此，需要对偏差进行修正。

\hat{M}_{t}=\frac{M_{t}}{1-\beta _{1}^{t}}

\hat{G}_{t}=\frac{G_{t}}{1-\beta _{2}^{t}}

Adam算法的参数更新差值为\bigtriangleup \theta_{t}=-\frac{\alpha }{\sqrt{\hat{G}_{t}+\epsilon } } \hat{M}_{t}

其中学习率通常设为0.001，并且也可以进行衰减，比如a_{t}=\frac{a_{0}}{\sqrt{t} }。

构建优化器?定义Adam类，继承Optimizer类
class Adam(Optimizer):
    def __init__(self, init_lr, model, beta1, beta2, epsilon):
        """
        Adam优化器初始化
        输入：
            - init_lr：初始学习率
            - model：模型，model.params存储模型参数值
            - beta1, beta2：移动平均的衰减率
            - epsilon：保持数值稳定性而设置的常数
        """
        super(Adam, self).__init__(init_lr=init_lr, model=model)
        self.beta1 = beta1
        self.beta2 = beta2
        self.epsilon = epsilon
        self.M, self.G = {}, {}
        for key in self.model.params.keys():
            self.M[key] = 0
            self.G[key] = 0
        self.t = 1
 
    def adam(self, x, gradient_x, G, M, t, init_lr):
        """
        adam算法更新参数
        输入：
            - x：参数
            - G：梯度平方的加权移动平均
            - M：梯度的加权移动平均
            - t：迭代次数
            - init_lr：初始学习率
        """
        M = self.beta1 * M + (1 - self.beta1) * gradient_x
        G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
        M_hat = M / (1 - self.beta1 ** t)
        G_hat = G / (1 - self.beta2 ** t)
        t += 1
        x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
        return x, G, M, t
 
    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
                                                                                 self.model.grads[key],
                                                                                 self.G[key],
                                                                                 self.M[key],
                                                                                 self.t,
                                                                                 self.init_lr)
2D可视化实验?使用被优化函数展示Adam算法的参数更新轨迹
                                                                                self.init_lr)
# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = Adam(init_lr=0.2, model=model, beta1=0.9, beta2=0.99, epsilon=1e-7)
train_and_plot_f(model, opt, epoch=20, fig_name='opti-vis-para5.pdf')

Adam算法可以自适应调整学习率，参数更新更加平稳。

2. 被优化函数?x^{2}/20+y^{2}??

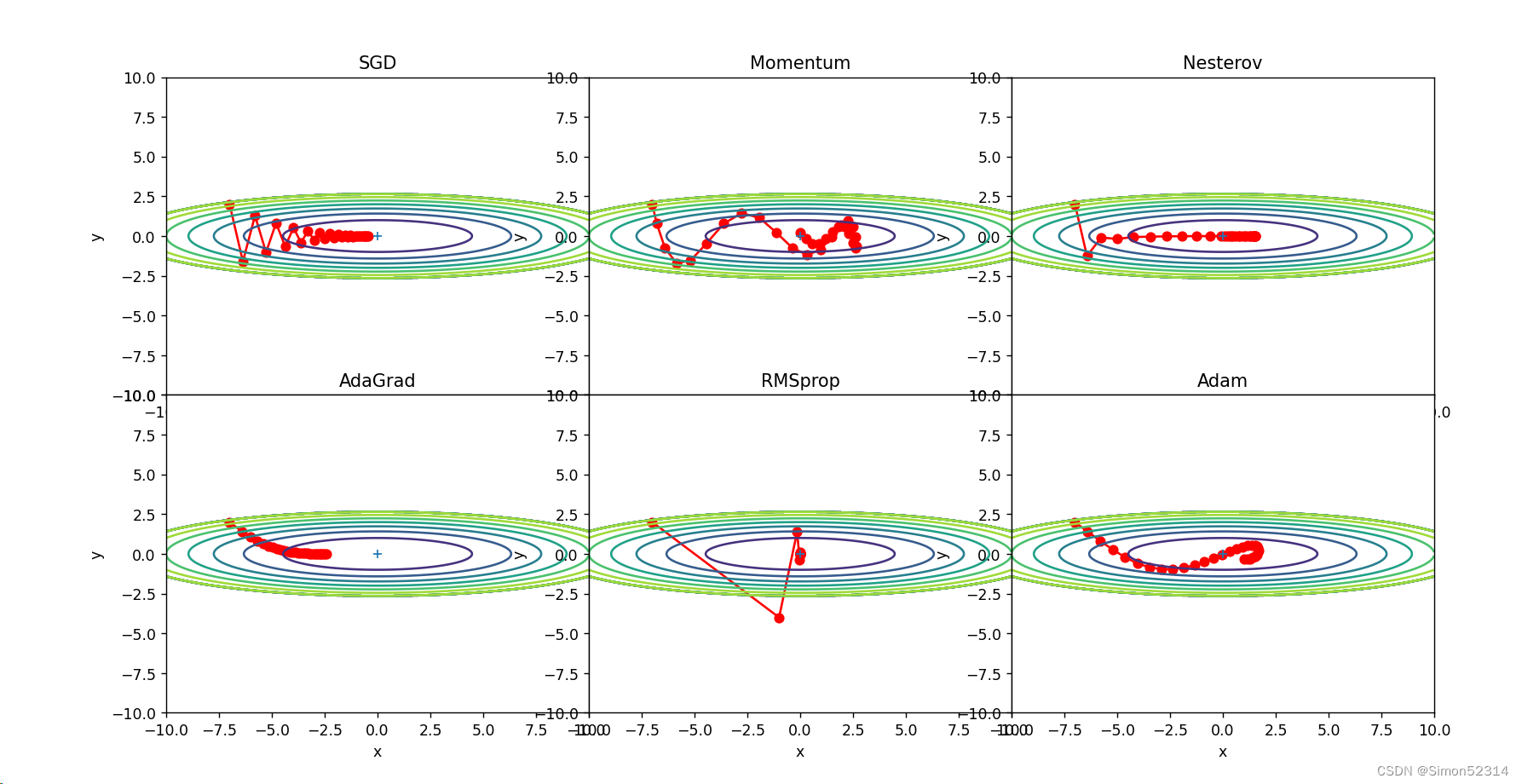
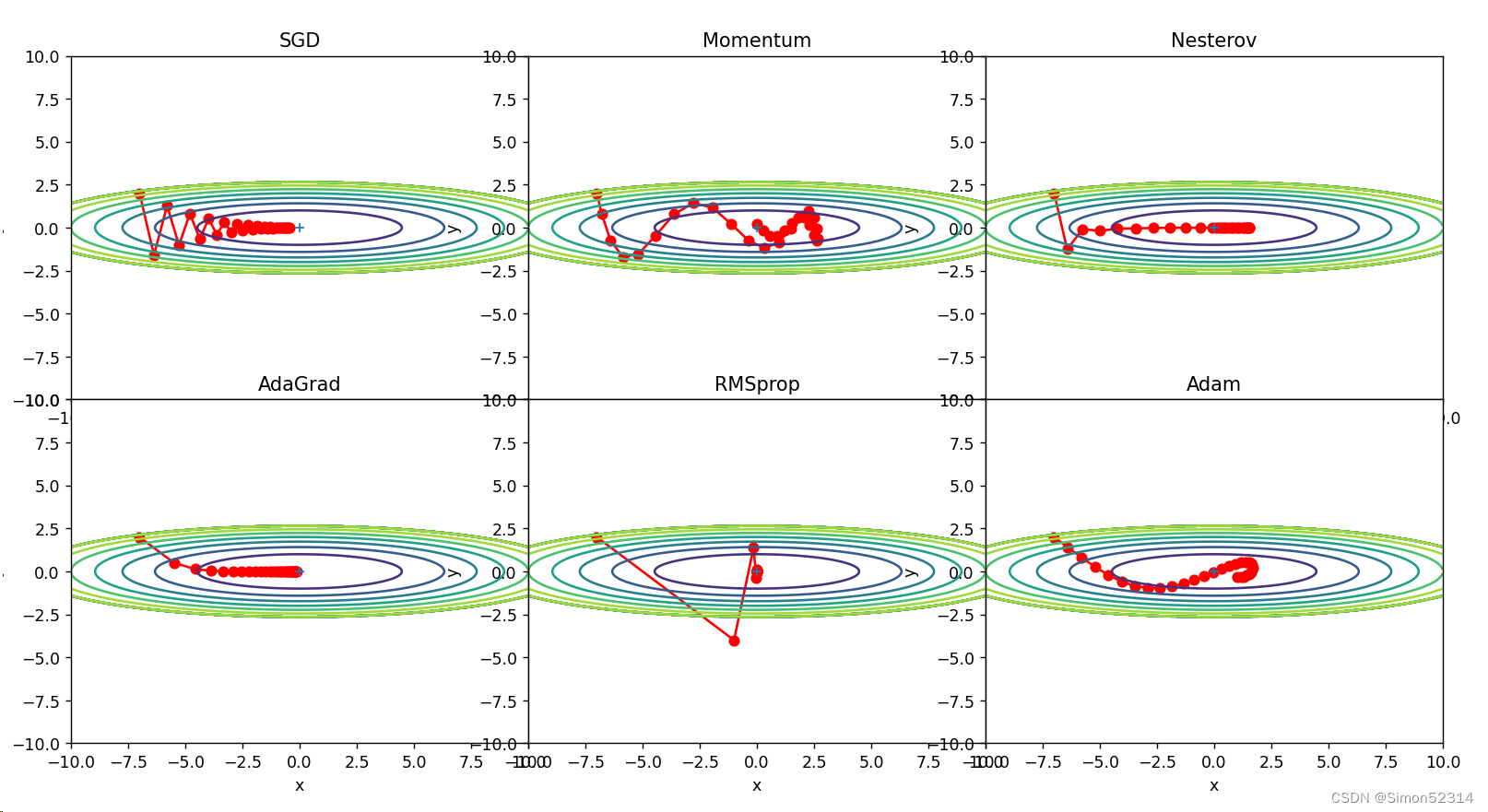
下图是老师给的效果图

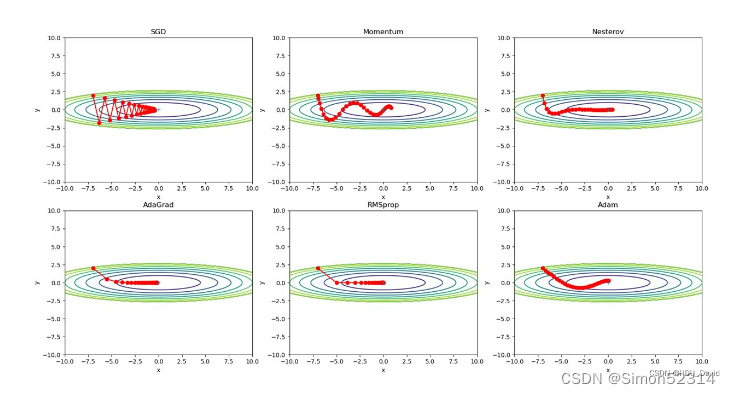
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict


class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]
class Momentum:
    """Momentum SGD（动量SGD）"""
    def __init__(self, lr=0.01, momentum=0.9):
        """初始化Momentum类，设置学习率为lr，动量为momentum。
        v是用于存储每个参数的动量值的字典。
        """
        self.lr = lr  # 学习率
        self.momentum = momentum  # 动量值
        self.v = None  # 存储参数动量值的字典

    def update(self, params, grads):
        """使用Momentum SGD更新参数。
        如果v为None，则初始化v字典。
        """
        if self.v is None:
            self.v = {}  # 初始化v字典
            for key, val in params.items():  # 遍历参数params的每个键值对
                self.v[key] = np.zeros_like(val)  # 为每个键在v字典中创建一个与对应参数形状相同的零数组

        for key in params.keys():  # 遍历params的每个键
            # 更新当前键的动量值，并减去学习率与梯度的乘积
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            # 更新当前键对应的参数值，加上动量值
            params[key] += self.v[key]
class Nesterov:
    """Nesterov's Accelerated Gradient (Nesterov's加速梯度法)"""
    def __init__(self, lr=0.01, momentum=0.9):
        """初始化Nesterov类，设置学习率为lr，动量为momentum。
        v是用于存储每个参数的动量值的字典。
        """
        self.lr = lr  # 学习率
        self.momentum = momentum  # 动量值
        self.v = None  # 存储参数动量值的字典
    def update(self, params, grads):
        """使用Nesterov's加速梯度法更新参数。
        如果v为None，则初始化v字典。
        """
        if self.v is None:
            self.v = {}  # 初始化v字典
            for key, val in params.items():  # 遍历参数params的每个键值对
                self.v[key] = np.zeros_like(val)  # 为每个键在v字典中创建一个与对应参数形状相同的零数组

        for key in params.keys():  # 遍历params的每个键
            # 更新当前键的动量值，乘以动量系数
            self.v[key] *= self.momentum
            # 减去学习率与梯度的乘积
            self.v[key] -= self.lr * grads[key]
            # 更新当前键对应的参数值，加上动量值乘以动量的平方和减去(1+动量)倍的学习率与梯度的乘积
            params[key] += self.momentum * self.momentum * self.v[key] - (1 + self.momentum) * self.lr * grads[key]
class AdaGrad:
    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSprop:
    """RMSprop优化器类"""

    def __init__(self, lr=0.01, decay_rate=0.99):
        """初始化RMSprop优化器

        Args:
            lr (float, optional): 学习率，默认为0.01
            decay_rate (float, optional): 衰减率，默认为0.99
        """
        self.lr = lr  # 学习率
        self.decay_rate = decay_rate  # 衰减率
        self.h = None  # 用于存储梯度平方的移动平均值的字典

    def update(self, params, grads):
        """更新参数

        Args:
            params (dict): 参数字典，键为参数名，值为参数值
            grads (dict): 梯度字典，键为参数名，值为对应参数的梯度值
        """
        if self.h is None:
            # 初始化h字典，形状与params中的参数相同，并填充为0
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            # 计算梯度平方的移动平均值
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            # 更新参数，使用梯度和其移动平均值的平方根来调整学习率
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)  # 添加1e-7是为了防止除数为0的情况


class Adam:
    """Adam (Adaptive Moment Estimation) 优化器类，参考论文：http://arxiv.org/abs/1412.6980v8)"""
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        """初始化Adam优化器
        Args:
            lr (float, optional): 学习率，默认为0.001
            beta1 (float, optional): 动量衰减率，默认为0.9
            beta2 (float, optional): 梯度平方的动量衰减率，默认为0.999
        """
        self.lr = lr  # 学习率
        self.beta1 = beta1  # 动量衰减率
        self.beta2 = beta2  # 梯度平方的动量衰减率
        self.iter = 0  # 迭代次数
        self.m = None  # 存储一阶矩（即梯度的平均值）的字典
        self.v = None  # 存储二阶矩（即梯度平方的平均值）的字典
    def update(self, params, grads):
        """更新参数
        Args:
            params (dict): 参数字典，键为参数名，值为参数值
            grads (dict): 梯度字典，键为参数名，值为对应参数的梯度值
        """
        if self.m is None:
            # 初始化一阶矩和二阶矩的字典，形状与params中的参数相同，并填充为0
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        self.iter += 1  # 增加迭代次数
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)  # 计算自适应学习率

        for key in params.keys():  # 遍历每个参数
            # 更新一阶矩（即梯度的平均值）和二阶矩（即梯度平方的平均值）
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
            # 使用自适应学习率和一阶矩、二阶矩来更新参数值
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)  # 添加1e-7是为了防止除数为0的情况
def f(x, y):
    return x ** 2 / 20.0 + y ** 2
def df(x, y):
    return x / 10.0, 2.0 * y
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0

learningrate = [0.9,0.3,0.3,0.6,0.6,0.6,0.6]
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=learningrate[0])
optimizers["Momentum"] = Momentum(lr=learningrate[1])
optimizers["Nesterov"] = Nesterov(lr=learningrate[2])
optimizers["AdaGrad"] = AdaGrad(lr=learningrate[3])
optimizers["RMSprop"] = RMSprop(lr=learningrate[4])
optimizers["Adam"] = Adam(lr=learningrate[5])

idx = 1
id_lr=0
for key in optimizers:
    optimizer = optimizers[key]
    lr = learningrate[id_lr]
    id_lr = id_lr + 1
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    # for simple contour line
    mask = Z > 7
    Z[mask] = 0

    # plot
    plt.subplot(2, 3, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)  # 绘制等高线
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")

plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
plt.show()

效果不太好太调一下学习率

3.?解释不同轨迹的形成原因

使用不同的优化算法产生不同运动轨迹的原因主要在于算法的优化机制和参数更新方式的不同，并且他们的学习率也不一样

分析各个算法的优缺点?
SGD

优点:简单直观，易于实现

? ? ? ? 对于线性模型效果很好

缺点:对初始学习率的选择比较敏感，如果初始学习率过大，可能会导致训练不稳定；

? ? ? ? 对于大数据集的处理速度较慢。

? ? ? ??容易陷入局部最优解

Momentum

优点:可以加速SGD收敛，抑制震荡。

? ? ? ? 在梯度方向改变时，能够降低参数更新速度，减少震荡；

? ? ? ?在梯度方向相同时，可以加速参数更新，从而加速收敛。

缺点:不适合更新参数变化剧烈的情况

? ? ? ? ?学习速率的初始值比较敏感

Adagrad

优点:可以对每个参数自适应地调整学习率

? ? ? ? 适用于稀疏数据 不需要手动调整学习率也能自适应调整学习率。

缺点:全局学习率需要人为设定，且随着训练的进行，学习率会逐渐增大，可能导致模型无法收敛。

RMSprop

优点:可以自适应地调整每个参数的学习率

? ? ? ? ?可以一定程度上解决 Adagrad 只会降低学习率的问题

缺点:学习率仍然会随着时间的推移而降低 RMSprop 不考虑梯度的偏移和峰值信息，可能导致某些方向上的梯度过大或过小

? ? ? ? ?在训练初期，参数的学习可能不够充分。

Adam

优点:结合了 Momentum 和 Adagrad 的优点

? ? ? ?可以自适应地调整每个参数的学习率和梯度指数衰减率

? ? ? ?对于大多数问题表现良好

缺点:对于低维度、稀疏数据和非平稳目标函数，可能导致表现不佳 不同超参数的组合，可能导致性能较差

今天写写这么多，好像还有一些选做题，明天补上，感觉这个博客太长了，期末复习看见这么长的会让我失去学习的欲望

总结：?

1、学习优化算法时，让我感受到了上学期学习的最优化算法给我这学期带来的一些基础。

2、每个优化算法在求同一个函数的最优解时候，需要的学习率不一样，这和他们的算法的优化机制和参数更新方式的不同，并且他们的学习率也不一样

3、写了这么多都是5个优化算法的原理和优缺点，所以对5个优化算法加深了了解

文章来源:https://blog.csdn.net/m0_62581697/article/details/135153064
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。