函数题：走方格

给定一个?n×m的方格阵，沿着方格的边线走，从左上角?(0,0)开始，每次只能往右或者往下走一个单位距离，问走到右下角?(n,m) 一共有多少种不同的走法。

输入格式

共一行，包含两个整数?n?和?m。

输出格式

共一行，包含一个整数，表示走法数量。

数据范围

1≤n,m≤10

输入样例：

2 3

输出样例：

10

?

?

?

#include <iostream>

using namespace std;

int n, m;//这两个要输入的数据都要定义在外面，因为在函数里面都会用到这两个值。
int ans;//老规矩，这个还是方案数。

void dfs(int x, int y)//这是定义的无返回值函数，因为这个原理几乎和dfs是一样的，所以函数名就直接是这个了。
{
    if (x == n && y == m)
        ans++; //这个相当于是终止条件，当满足这个条件的时候，那么就代表着一种行走方案的结束，要进行下一种了。
    if (x < n)
        dfs(x + 1, y);
        //这是向下走的条件
    if (y < m)
        dfs(x, y + 1);
    //这是向右走的条件
}
int main()
{
    cin >> n >> m;
    dfs(0, 0);//这里其实就是初始化x，y，意思就是从(0,0)这个点开始走。
    cout << ans << endl;

    return 0;
}

总结：这个题和那个跳台阶是一个类型的，只不过从一维变成了二维，变成了坐标的形式而已，但是，经过这两个题后，我自己有了一些自己的理解和看法。

? 这两个题其实都是用dfs，就是深度优先搜索，用的是递归的思想。递归，听起来就觉得难，我也这样觉得，但是做了这两个题之后，我觉得其实我们侧重点应该调整，我们不应该执着于去完全理解递归，而应该注重做题的思路和逻辑，这样就不会因为无法完全理解递归的思想而放弃了。

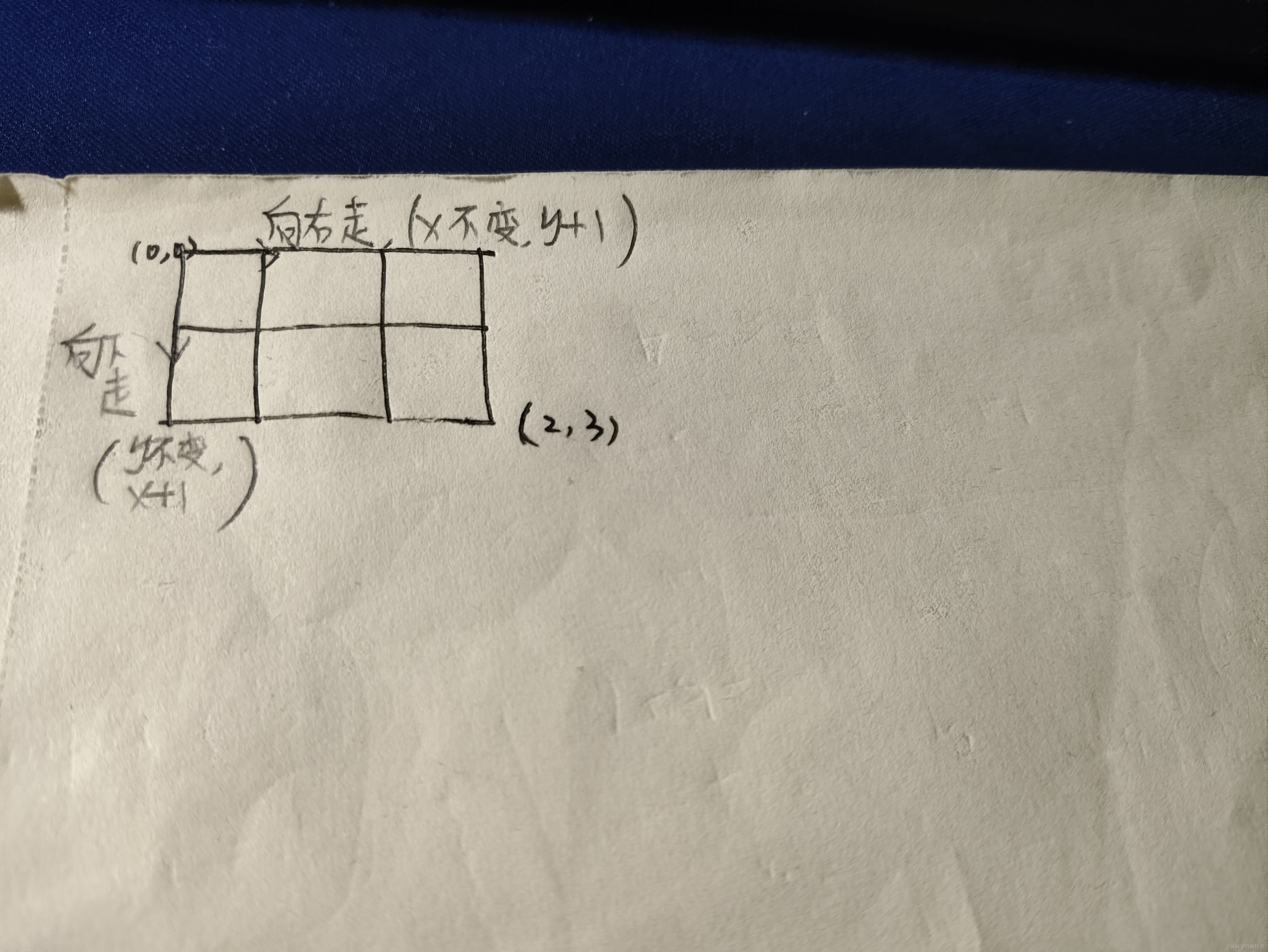
? ?好了，来说说感悟吧，这个题其实说的很明确，点从(0,0)开始，每次只能往右走或者往下走，这句话就是函数里面的递归语句。对于这个题，我们不要想怎么递归，直接想思路：点从(0,0)开始，我们先只考虑往下走的情况，我们发现，往下走的时候，y是不变的，只有x在不断增加，因为是每次只能走一格，所以每次x都加1，直到不能往下走为止。举个例子，看我上面的那个过程图，会发现，当n=2,y=3时，走到(2,0)这个点时，它就不能往下面走了，所以这个点我们不要，所以才会得到那个if语句里面的条件：if(x<n) ?dfs(x+1,y);另外一种往右走也是这样分析的，所以我们就得到了那上面的if语句，来判断情况。

? ? 这就是这个题的思路，就直接写在那个函数里面，只不过要注意的是，因为是递归，所以坐标的变化不能仅仅用变量+1就行，得写成调用函数的形式，这样就相当与自己调用自己，这其实就是递归了，就这样，我们只写了一个函数，在里面写上自己的思路，然后数据变化调用函数计算，这样自然而然就完成了代码，也实现了递归的运行，用这样的想法去做这个题，那理解起来就简单多了。

如果要自己画图一条一条的数的话，又累人，又有可能数错，这是不建议的，直接写思路就行了。

? ok，这就是我的理解和感悟，就这么多了。