leetcode 股票DP系列 总结篇

121. 买卖股票的最佳时机

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。
只能进行一次交易
很简单，只需边遍历边记录最小值即可。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
        for (int i = 0, minp = INT_MAX; i < prices.size(); i ++ ) {
            res = max(res, prices[i] - minp);
            minp = min(minp, prices[i]);
        }
        return res;
    }
};

122. 买卖股票的最佳时机 II

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。
不限制交易次数

class Solution {
    public int maxProfit(int[] prices) {
//不论如何交易都等价于连续进行单天买入卖出的交易
//pi-pj=pi-pk+pk-pj
//只加正数天即可
       int res=0;
       for(int i=0;i+1<prices.length;i++){
           res+=Math.max(0,prices[i+1]-prices[i]);
       }
       return res;
    }
}

123. 买卖股票的最佳时机 III

你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
限制交易次数
任何时候最多一次只能持有一只股票
思路一:
前后缀分解, 枚举第二次交易买入的时间
前半段就是1~ i - 1天只进行一次交易的最大收益(预处理出来一个f数组，实际上就是121题)
想要提前知道什么东西只能预处理，或者贪心（猜），或者二分，先猜想答案再去验证
右边就是 maxRight - i

class Solution {
    public int maxProfit(int[] prices) {
           int n=prices.length;
           int[] f=new int[n];
           int leftMin=prices[0];
           f[0]=0;//f[i] [0,i]天进行一次交易的最大值
           for(int i=1;i<n;i++){
               f[i]=Math.max(f[i-1],prices[i]-leftMin);
               leftMin=Math.min(leftMin,prices[i]);           
           }
           int res=0;
           int rightMax=prices[n-1];
           for(int i=n-1;i>=0;i--){//最右的特殊情况是只做一次交易，只有前缀
               if(i!=0)
               //注： 这里为什么不改成Math.max(rightMax - prices[i], 0);
               //因为假如有半部分这个值<0了，也就只是说明f[i - 1]会失效，
               //i.e. f[i - 1]加了个负数
               //也就是说我们没有考虑只采用f[i - 1]的情况，
               //但是这个情况已经包含最左，只有一个后缀，只进行一次交易的情况中了,也就是包含在res=Math.max(res,rightMax-prices[i]);中了
               res=Math.max(res,f[i-1]+rightMax-prices[i]);
               else
               res=Math.max(res,rightMax-prices[i]);
               rightMax=Math.max(rightMax,prices[i]);
           }
           return res;
    }
}

另一种更通用的方法: 动态规划
以下的代码可能有点难理解，不如画成状态机
之后的总结建议看：
灵茶山艾府

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int buy1 = -prices[0], sell1 = 0;
        int buy2 = -prices[0], sell2 = 0;
        for (int i = 1; i < n; ++i) {
            buy1 = Math.max(buy1, -prices[i]);
            sell1 = Math.max(sell1, buy1 + prices[i]);
            buy2 = Math.max(buy2, sell1 - prices[i]);
            sell2 = Math.max(sell2, buy2 + prices[i]);
        }
        return sell2;
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/solutions/552695/mai-mai-gu-piao-de-zui-jia-shi-ji-iii-by-wrnt/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

188

至多k次交易
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

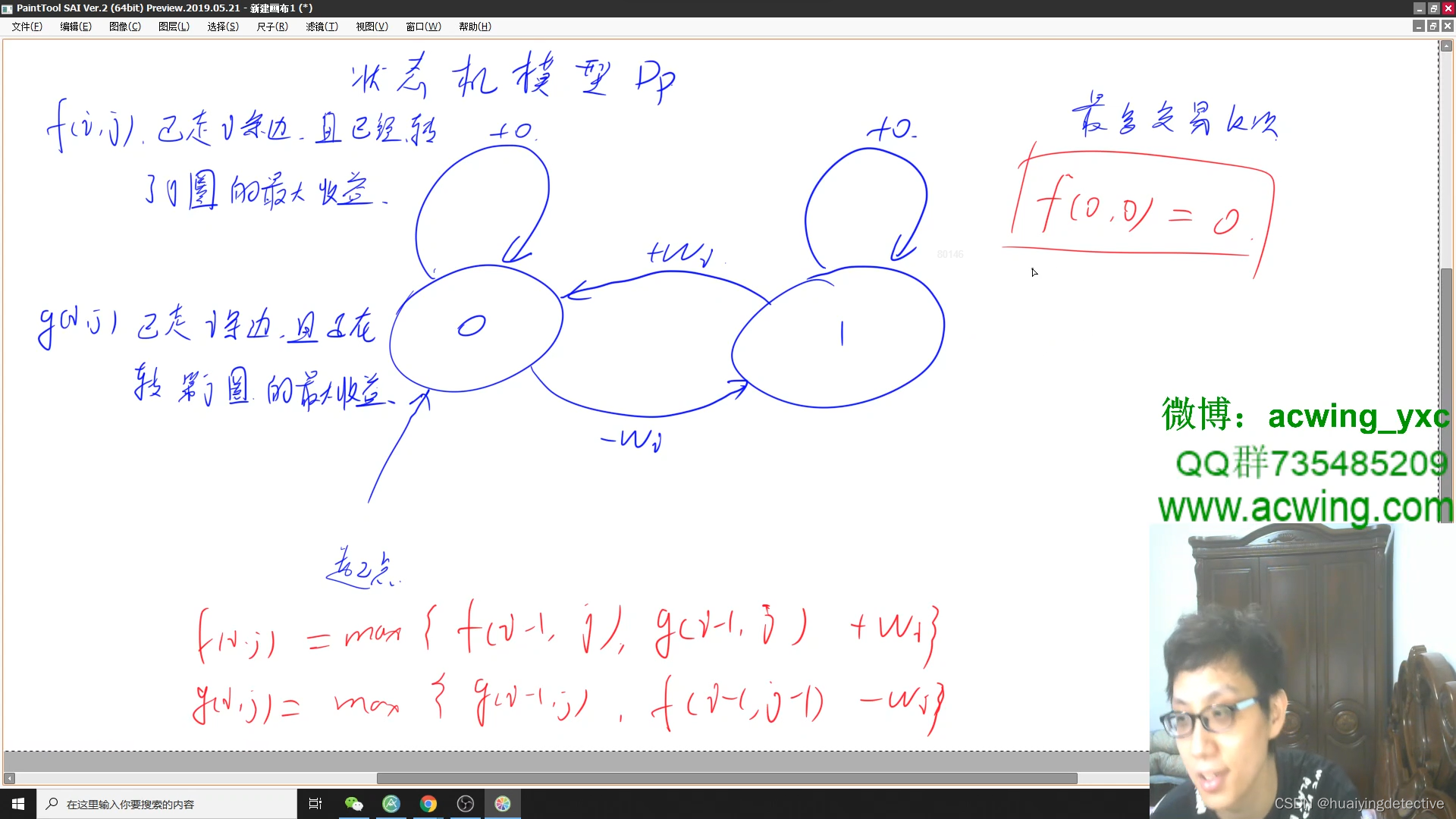
大雪菜
灵茶山做法可能更好记：

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        int[][][] f = new int[n + 1][k + 2][2];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= k + 1; j++) {
                Arrays.fill(f[i][j], Integer.MIN_VALUE / 2); // 防止溢出
            }
        }
        for (int j = 1; j <= k + 1; j++) {
            f[0][j][0] = 0;
        }
        for (int i = 0; i < n; i++) {
            for (int j = 1; j <= k + 1; j++) {
                f[i + 1][j][0] = Math.max(f[i][j][0], f[i][j][1] + prices[i]);
                f[i + 1][j][1] = Math.max(f[i][j][1], f[i][j - 1][0] - prices[i]);
            }
        }
        return f[n][k + 1][0];
    }
}

作者：灵茶山艾府
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/solutions/2201488/shi-pin-jiao-ni-yi-bu-bu-si-kao-dong-tai-kksg/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
class Solution {
    public int maxProfit(int k, int[] prices) {
        int[][] f = new int[k + 2][2];
        for (int j = 1; j <= k + 1; j++) {
            f[j][1] = Integer.MIN_VALUE / 2; // 防止溢出
        }
        f[0][0] = Integer.MIN_VALUE / 2;
        for (int p : prices) {
            for (int j = k + 1; j > 0; j--) {
                f[j][0] = Math.max(f[j][0], f[j][1] + p);
                f[j][1] = Math.max(f[j][1], f[j - 1][0] - p);
            }
        }
        return f[k + 1][0];
    }
}

作者：灵茶山艾府
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/solutions/2201488/shi-pin-jiao-ni-yi-bu-bu-si-kao-dong-tai-kksg/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

309 最佳买卖股票时机含冷冻期

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意股票系列状态总是 f[i] 表示第 i 天结束之后的状态
这里的「处于冷冻期」指的是在第 i 天结束之后的状态。也就是说：如果第 i 天结束之后处于冷冻期，那么第 i+1天无法买入股票。

class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length == 0) {
            return 0;
        }

        int n = prices.length;
        // f[i][0]: 手上持有股票的最大收益
        // f[i][1]: 手上不持有股票，并且处于冷冻期中的累计最大收益
        // f[i][2]: 手上不持有股票，并且不在冷冻期中的累计最大收益
        int[][] f = new int[n][3];
        f[0][0] = -prices[0];
        for (int i = 1; i < n; ++i) {
            f[i][0] = Math.max(f[i - 1][0], f[i - 1][2] - prices[i]);
            f[i][1] = f[i - 1][0] + prices[i];
            f[i][2] = Math.max(f[i - 1][1], f[i - 1][2]);
        }
        return Math.max(f[n - 1][1], f[n - 1][2]);
    }
}

// 作者：力扣官方题解
// 链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/solutions/323509/zui-jia-mai-mai-gu-piao-shi-ji-han-leng-dong-qi-4/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

714. 买卖股票的最佳时机含手续费

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/
类似122, 唯一的区别就在于本题有「手续费」而第 122 题没有。
灵茶山

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        int[][] dp = new int[n][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for (int i = 1; i < n; ++i) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[n - 1][0];
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/solutions/524669/mai-mai-gu-piao-de-zui-jia-shi-ji-han-sh-rzlz/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
class Solution {
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        int sell = 0, buy = -prices[0];
        for (int i = 1; i < n; ++i) {
            sell = Math.max(sell, buy + prices[i] - fee);
            buy = Math.max(buy, sell - prices[i]);
        }
        return sell;
    }
}

作者：力扣官方题解
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/solutions/524669/mai-mai-gu-piao-de-zui-jia-shi-ji-han-sh-rzlz/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

1911. 最大子序列交替和

https://leetcode.cn/problems/maximum-alternating-subsequence-sum/

class Solution {
    public long maxAlternatingSum(int[] nums) {
        // p[i] 结尾为正数的序列的最大和 p[i - 1], g[i - 1] + nums[i]
        // g[i] 结尾为负数的序列的最大和 
        int n = nums.length;
        long[] p =new long[2];
        long[] g = new long[2];
        p[0] = Integer.MIN_VALUE / 2;
        g[0] = 0;//初始的时候 第一个选择的数字必然是正数， 因此在开始循环之前结尾为负数的序列是合法的
        for(int i = 1; i <= n; i++) {
            //滚动数组小技巧
            p[i & 1] = Math.max(p[(i - 1) & 1], g[(i - 1) & 1] + nums[i - 1]);
            g[i & 1] = Math.max(g[(i - 1) & 1], p[(i - 1) & 1] - nums[i - 1]);
        }
        return p[n & 1];
    }
}

方法二
func maxAlternatingSum(nums []int) int64 {
	f := [2]int{0, math.MinInt64 / 2} // 除 2 防止计算时溢出
	for _, v := range nums {
		f = [2]int{max(f[0], f[1]-v), max(f[1], f[0]+v)}
	}
	return int64(f[1])
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

作者：灵茶山艾府
链接：https://leetcode.cn/problems/maximum-alternating-subsequence-sum/solutions/846375/dong-tai-gui-hua-by-endlesscheng-d92a/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。