【Matlab】PSO-BP 基于粒子群算法优化BP神经网络的数据时序预测(附代码)
?资源下载:?https://download.csdn.net/download/vvoennvv/88689096
一,概述
? ? ? ? PSO-BP算法是一种结合了粒子群算法(PSO)和BP神经网络的方法,用于数据时序预测。下面是PSO-BP算法的原理和过程:
? ? ? ? 1. 数据准备:首先,将时序数据按照一定的时间窗口划分为输入序列和输出序列。例如,可以将过去几个时间步的数值作为输入,预测未来一个时间步的数值作为输出。
? ? ? ? 2. 初始化粒子群:对于PSO-BP算法,需要初始化一组粒子,每个粒子代表了BP神经网络的一组权重和阈值参数。每个粒子都有自己的位置和速度。
? ? ? ? 3. 评估适应度:对于每个粒子,需要根据其位置的权重和阈值参数构建BP神经网络,并使用历史数据进行训练。训练完成后,使用预测误差的指标(如均方误差)来评估粒子的适应度。
? ? ? ? 4. 更新粒子的个体最优位置:根据评估的适应度值,更新每个粒子的个体最优位置。保留具有最佳适应度的解作为粒子的个体最优位置。
? ? ? ? 5. 更新群体最优位置:根据所有粒子的个体最优位置,确定全局最优位置,即群体最优位置。这是整个粒子群中适应度最好的解。
? ? ? ? 6. 更新粒子的速度和位置:根据粒子群算法的速度更新公式,更新粒子的速度和位置。速度的更新会考虑到个体最优位置和群体最优位置之间的差异。
? ? ? ? 7. 使用BP算法进行训练:基于更新后的权重和阈值参数,使用BP算法对神经网络进行训练。这一步是为了进一步优化粒子的解,使得BP神经网络能够更好地捕捉时序数据的模式和趋势。
? ? ? ? 8. 重复步骤3-7:重复执行步骤3到步骤7,直到满足停止条件(如达到最大迭代次数或达到一定的预测精度要求)。
? ? ? ? 通过粒子群的迭代和优化过程,PSO-BP算法可以不断调整BP神经网络的权重和阈值参数,以最小化预测误差,并实现对时序数据的有效预测。这种结合了全局搜索和局部搜索的方法可以提高数据时序预测的准确性,适用于许多实际应用场景。但是需要注意,PSO-BP算法的性能还受到超参数选择和训练数据的质量等因素的影响,需要进行合理调整和优化。
?
二,代码
代码中文注释非常清晰,按照示例数据修改格式,替换数据集即可运行,数据集为excel。
部分代码如下:
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
%% 导入数据(时间序列的单列数据)
result = xlsread('数据集.xlsx');
%% 数据分析
num_samples = length(result); % 样本个数
kim = 15; % 延时步长(kim个历史数据作为自变量)
zim = 1; % 跨zim个时间点进行预测
%% 构造数据集
for i = 1: num_samples - kim - zim + 1
res(i, :) = [reshape(result(i: i + kim - 1), 1, kim), result(i + kim + zim - 1)];
end
%% 数据集分析
outdim = 1; % 最后一列为输出
num_size = 0.7; % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度
%% 划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 节点个数
inputnum = size(p_train, 1); % 输入层节点数
hiddennum = 5; % 隐藏层节点数
outputnum = size(t_train, 1); % 输出层节点数
%% 建立网络
net = newff(p_train, t_train, hiddennum);
%% 设置训练参数
net.trainParam.epochs = 1000; % 训练次数
net.trainParam.goal = 1e-6; % 目标误差
net.trainParam.lr = 0.01; % 学习率
net.trainParam.showWindow = 0; % 关闭窗口
%% 参数初始化
c1 = 4.494; % 学习因子
c2 = 4.494; % 学习因子
maxgen = 30; % 种群更新次数
sizepop = 5; % 种群规模
Vmax = 1.0; % 最大速度
Vmin = -1.0; % 最小速度
popmax = 2.0; % 最大边界
popmin = -2.0; % 最小边界
%% 节点总数
numsum = inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum;
for i = 1 : sizepop
pop(i, :) = rands(1, numsum); % 初始化种群
V(i, :) = rands(1, numsum); % 初始化速度
fitness(i) = fun(pop(i, :), hiddennum, net, p_train, t_train);
end
%% 个体极值和群体极值
[fitnesszbest, bestindex] = min(fitness);
zbest = pop(bestindex, :); % 全局最佳
gbest = pop; % 个体最佳
fitnessgbest = fitness; % 个体最佳适应度值
BestFit = fitnesszbest; % 全局最佳适应度值
......三,运行结果
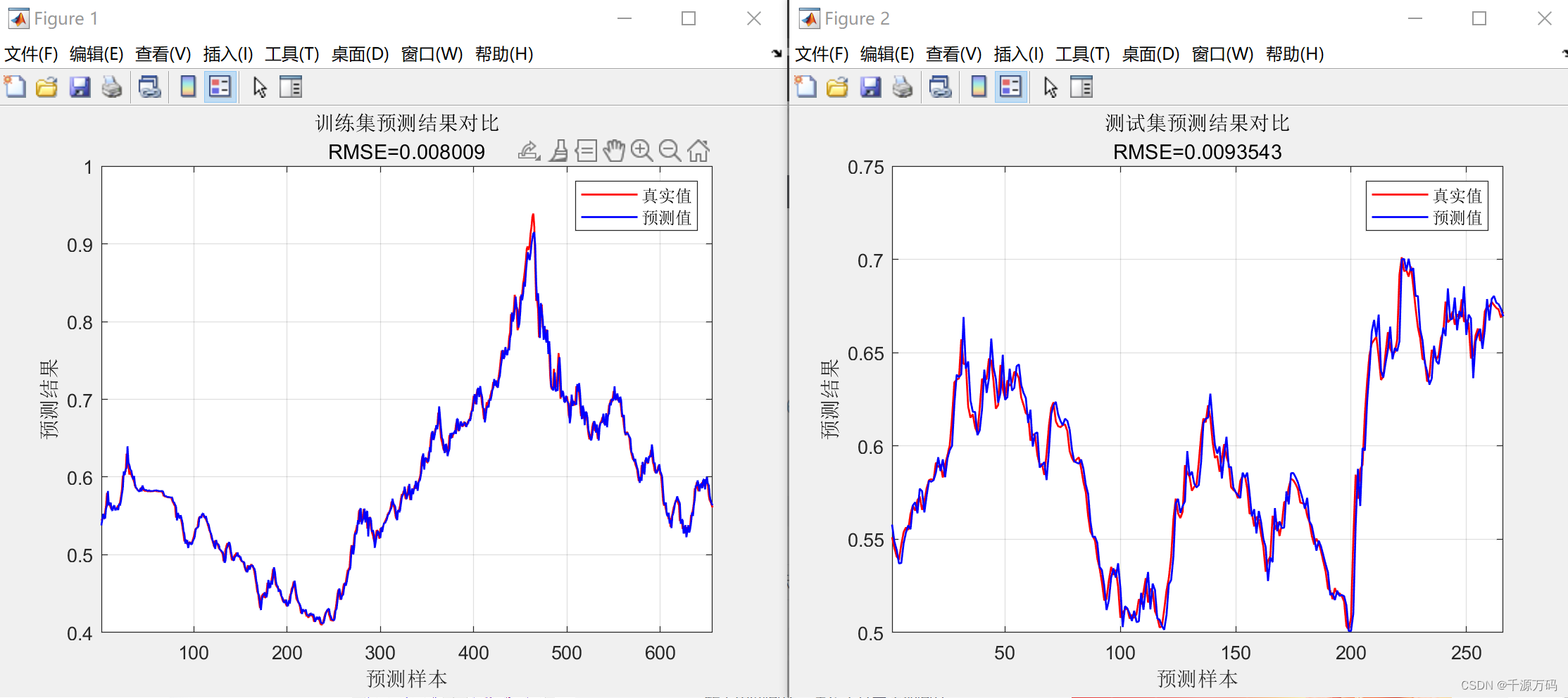


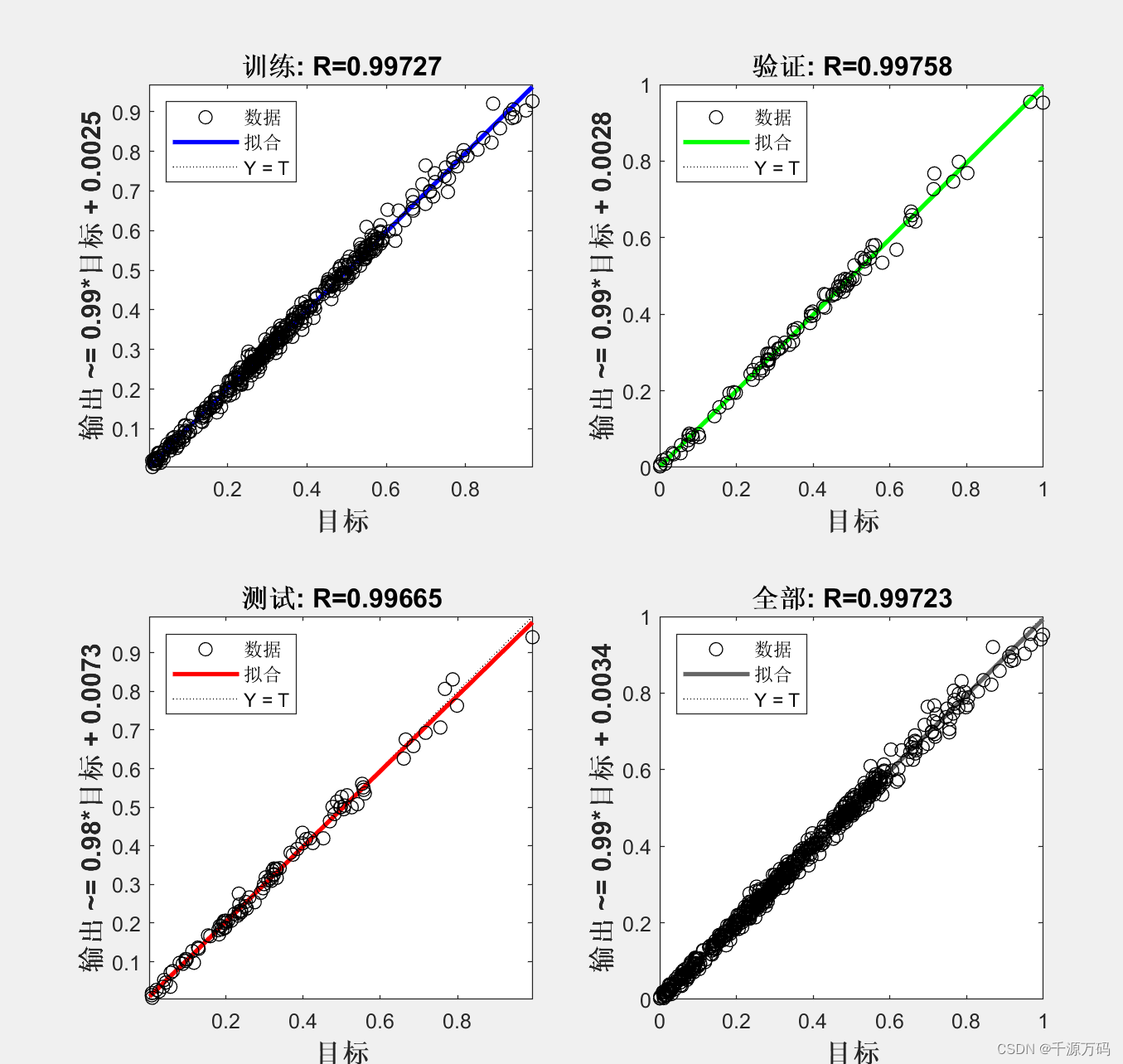
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!