算法设计与分析复习笔记第三章动态规划

第三章 动态规划

最短路径

将待求解问题分解为若干子问题，通过子问题的解得到原问题的解，这是问题求解的有效途径。但是如何实施分解？

分治策略的基本思想是将规模为n的问题分解为k个规模较小的子问题，各子问题相互独立但与原问题求解策略相同。并不是所有问题都可以这样处理。

问题分解的另一个途径是将求解过程分解为若干阶段（级），依次求解每个阶段即得到原问题的解。通过分解得到的各子阶段不要求相互独立，但希望它们具有相同类型，而且前一阶段的输出可以作为下一阶段的输入。这种策略特别适合求解具有某种最优性质的问题。

贪心法属于这类求解策略：对问题P(n)，其求解过程中各贪心选择步骤构成决策序列
D=<D1,D2,..Dk>。Di的最优性仅依赖于D1,D2,..Di-1。贪心法不保证决策序列D最后求出解的最优性。

动态规划

动态规划也是一个分阶段判定决策过程，其问题求解策略的基础是决策过程的最优原理：为达到某问题的最优目标T，需要依次作出决策序列D=<D1,…Dk>。如果D是最优的，则对任意i(1≤i<k)，决策子序列Di+1,…Dk也是最优的，即当前决策的最优性取决于其后续决策序列的是否最优。由此追溯至目标，再由最终目标决策向上回溯，导出决策序列 D=<D1,…Dk>，因此动态规划方法可以保证问题求解是全局最优的。

也可以这样理解：如果求最优解的问题可以划分成若干段（级），那么最后求得的最优解是由各个部分解所组成，而这些部分解一定是对应阶段的最优解。

最短路径

给定简单有向连通赋权图G=<V,E,w>，w(i,j)是G中边<i,j>的权。顶点集V可以划分为k+1个两两不交的子集Vi，i =0,1,2,..k。其中V0={s}，Vk={t}。对G中任一边<u,v>，存在Vi、Vi+1，使得u属于Vi，v属于Vi+1，其中0≤i<k。称G为k段图，s点为起点，t为终点。

一个多段图的例子

记D(u,v)是G中起点为u,终点为v的最短路径，C(u,v)是该路径上各边权的和。
设D(s,t)= <s,vi1,vi2…vik-1,t>，vir属于Vr（r=1,2..k-1），则D(vi1,t)= <vi1,vi2,…vik-1,t>是从vi1出发到t的最短路径，D(vi2,t)= <vi2,…vik-1,t>是从vi2出发到t的最短路径等等。设u属于Vi，有：

C(u,t)=min{w(u,v)+C(v,t)} v∈Vi+1 （4.1）

阶段4: C(7,t)=w(7,t)=8，C(8,t)=w(8,t)=4

阶段3: C(4,t)=min{w(4,7)+C(7,t), w(4,8)+C(8,t)}=12
C(5,t)=min{w(5,7)+C(7,t), w(5,8)+C(8,t)}=10
C(6,t)=min{w(6,7)+C(7,t), w(6,8)+C(8,t)}=8

阶段2： C(1,t)=min{w(1,4)+C(4,t), w(1,5)+C(5,t)}=19
C(2,t)=min{w(2,4)+C(4,t), w(2,5)+C(5,t), w(2,6)+C(6,t)}=17
C(3,t)=min{w(3,5)+C(5,t), w(3,6)+C(6,t)}=13

阶段1: C(s,t)=min{w(s,1)+C(1,t), w(s,2)+C(2,t), w(s,3)+C(3,t)}=16

沿求解中带下划线的项回溯，得最短路径解：D(s,t)= <s,3,5,8,t>

问题解决关键

求解过程中起到关键作用的是公式(4.1)，它给出了求该问题最优解的基本性质：原始问题最优解与子问题的最优解存在递归关系，称这种关系为问题的最优子结构。最优子结构为构造求解问题的最优决策序列提供了重要线索，它提示可以自底向上的方式逐次由子问题最优解构造原始问题的最优解。

公式(4.1)还有一个重要特征：由给出的自顶向下的递归分解中，每次产生的子问题求解的关键（例如，求C(v,t)）与原问题是类似的，只是在相对较小的子问题空间中考虑问题的解，因此子问题与原始问题存在相似性。而且这些子问题的解在不同的上一级问题中都需要用到，这种特征可以称为子问题重叠。

采用邻接矩阵表示图G，其中wij为G中边<i,j>的权，如果<i,j>不是G的边, 则wij=∞。G的节点集V={0,1,2,…n}，其中V0={0}是起始点集，Vk={n}是终点集，{V0,V1,…Vk}中各子集非空、两两不交。设V1={1，2，..r1}，V2={ r1+1，r1+2，… r2}，…Vk-1={ rk-2+1，rk-2+2，.. (n-1)}。

【算法3-1】MultiStage_Graph

S1: 初始化：j=n-1；对i=0,1,…n，ci=0； // ci为节点i到终点n的最短路径长
S2: 求节点r，使得wjr+cr=min{wji+ci|<j,i>是G的边}; //按照{V0,V1,…Vk}对节点的标记，j<i。
S3: cj=wjr+cr, Dj=r; // Dj=r 表示边<j,r>是从j出发到n的最短路径上第1条边?
S4: j=j-1;
S5: 如果j≥0则转S2;
S6: 输出从源点0出发的最短路径长c0 ；p0=0, pk=n;
S7: 对j=1,2,…k，pj=Dpj-1; //最短路径Path=< p0, p1,…pk>

MultiStage_Graph算法复杂度

G用邻接矩阵表示，对于S2到S5的主循环执行n次。为求满足wjr+cr=min{wji+ci|<j,i>是G的边}的r，最多要求n-1次比较。因此时间复杂性为O(n2)。除输入G，输出P外，要求附加存储空间c、D。

如果G采用邻接表表示，求满足最小性的节点r仅对属于G的边<j,r>访问一次，此算法的时间复杂性应该为O(n+e)（e为G的边数）。

一般地，为避免递归过程中的重复计算，每个子问题首次处理时将结果保存以备查。在上面的过程中，每一次求得的cj都必须记录下来。

从源点往后推

算法4-1完全是从汇点往前推，实际上我们也可以用同样的思想，从源点出发往后推。

阶段1: C(s,1)=w(s,1)=4， C(s,2)=w(s,2)=2,???C(s,3)=w(s,3)=3

阶段2: C(s,4)=min{w(1,4)+C(s,1), w(2,4)+C(s,2)}=min{14,8}= 8
C(s,5)=min{w(1,5)+C(s,1), w(2,5)+C(s,2), w(3,5)+C(s,3)}=min{13,9,6}= 6
C(s,6)=min{w(2,6)+C(s,2), w(3,6)+C(s,3)}=min{12,11}= 11

阶段3: C(s,7)=min{w(4,7)+C(s,4), w(5,7)+C(s,5), w(6,7)+C(s,6)} =min{12,15,16}= 12
C(s,8)=min{w(4,8)+C(s,4), w(5,8)+C(s,5), w(6,8)+C(s,6)} =min{16,12,15}= 12

阶段4: C(s,t)=min{w(7,t)+C(s,7), w(8,t)+C(s,8)}=min{20,16}= 16

图中任意两点间的最短距离

如果上面的图不是分段图，仍然可以用此方法来求图中任意两点间的最短路径，这就是大名鼎鼎的Floyd算法。程序段如下：

矩阵连乘

矩阵连乘问题

给定n个矩阵：A1, A2, …, An，其中Ai与Ai+1是可乘的。确定一种连乘的顺序，使得矩阵连乘的计算量为最小。

设A和B分别是p×q和q×r的两个矩阵，则乘积C=AB为p×r的矩阵，计算量为pqr次数乘。

但是对于多于2个以上的矩阵连乘，连乘的顺序却非常重要，因为不同的顺序的总计算量将会有很大的差别。

不同计算顺序的差别

设矩阵A1, A2和A3分别为10×100, 100×5和5×50的矩阵，现要计算A1A2A3 。

若按((A1A2)A3)来计算，则需要的数乘次数为10×100×5 + 10×5×50 = 7500

若按(A1(A2 A3))来计算，则需要的数乘次数为100 ×5 ×50+ 10×100×50 = 75000

后一种计算顺序的计算量竟是前者的10倍！

所以，求多个矩阵的连乘积时，计算的结合顺序是十分重要的。

不同计算顺序的数量

设n个矩阵的连乘积有P(n)个不同的计算顺序。

先在第k个和第k+1个矩阵之间将原矩阵序列分成两个矩阵子序列，k=1,…,n；再分别对两个子序列完全加括号，最后对结果加括号，便得到原序列的一种完全加括号方式。

由此可得出关于P(n)的递归式：

解此递归方程可得P(n) = C(n–1)，其中

所以P(n)随n的增长呈指数增长。因而穷举搜索法不是有效的算法。

分解最优解的结构

将矩阵连乘积AiAi+1…Aj记为A[i: j]。

若A[1: n] 的一个最优解是在矩阵Ak和Ak+1处断开的，即A[1: n] = (A[1: k] A[k+1: n])，则A[1: k]和A[k+1: n]也分别是最优解。

事实上，若A[1: k]的一个计算次序所需计算量更少的话，则用此计算次序替换原来的次序，则得到A[1: n]一个更少的计算量，这是一个矛盾。同理A[k+1: n]也是最优解。

最优子结构性质：最优解的子结构也最优的。

建立递归关系

令m[i][j] , 1≤i, j≤n，为计算A[i, j] 的最少数乘次数，则原问题为m[1][n]。

当i = j时，A[i, j]为单一矩阵， m[i][j] = 0；当i＜j时，利用最优子结构性质有：

Pi-1pkpj:左边矩阵连乘得到的矩阵与右边矩阵连乘得到的矩阵相乘的计算次数

直接递归的时间复杂性

数学归纳法证明T(n)≥2n–1 = Ω(2n)。

直接递归算法的时间复杂性随n的指数增长。

直接递归中有大量重复计算

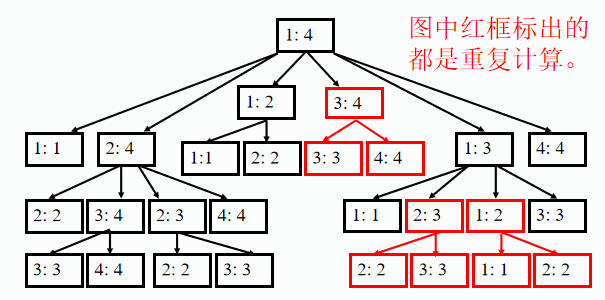
消除重复的计算

要消除重复计算，可在计算过程中保存已解决的子问题的答案。这样，每个子问题只计算一次，而在后面需要时只要简单查一下，从而避免重复计算。

计算方式可依据递归式自底向上地进行。

注意到在此问题中，不同的有序对 (i, j)就对应不同的子问题，因此不同的子问题个数最多只有Cn2+ n = Θ(n2)个。

自底向上的计算

消除重复的矩阵连乘算法

MatrixChain的运行举例

m[i][j] , 1≤i, j≤n，为计算A[i, j] 的最少数乘次数

s[i][j]计算A[i, j] 的最少数乘次数时的断点

MatrixChain的时间复杂性

算法MatrixChain的主要计算取决于程序中对r、i和k的三重循环。循环体内的计算量为O(1)，1≤ r、i、k≤n，三重循环的总次数为O(n3)。因此该算法时间复杂性的上界为O(n3)，比直接递归算法要有效得多。算法使用空间显然为O(n2)。这种算法称为动态规划。

动态规划的基本思想

将原问题分解为若干个子问题，先求子问题的解，然后从这些子问题的解得到原问题的解。

这些子问题的解往往不是相互独立的。在求解的过程中，许多子问题的解被反复地使用。为了避免重复计算，动态规划算法采用了填表来保存子问题解的方法。

在算法中用表格来保存已经求解的子问题的解，无论它是否会被用到。当以后遇到该子问题时即可查表取出其解，避免了重复计算。

动态规划的基本要素

最优子结构：问题的最优解是由其子问题的最优解所构成的。

最优子结构性质使我们能够以自底向上的方式递归地从子结构的最优解构造出问题的最优解。

重叠子问题：子问题之间并非相互独立的，而是彼此有重叠的。

因为子问题重叠，所以存在着重复计算。这样就可以用填表保存子问题解的方法来提高效率。

动态规划与贪心算法的比较

相同点：都具有最优子结构性质。

不同点：
贪心算法具有贪心选择性质；动态规划算法具有子问题重叠性，子问题空间小；
动态规划算法通常以自底向上的方式解各子问题；贪心算法则通常以自顶向下的方式进行，以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题。

可用贪心算法时，动态规划方法可能不适用；

可用动态规划方法时，贪心算法可能不适用。

动态规划的基本方法

动态规划通常可以按以下几个步骤进行：
(1)找出最优解的性质，并刻画其结构特征；
(2)递归地定义最优值；
(3)以自底向上的方式计算出各子结构的最优值并添入表格中保存；
(4)根据计算最优值时得到的信息，构造最优解。
步骤1~3是动态规划算法的基本步骤。若需要最优解，则必须执行第4步，为此还需要在第3步中记录构造最优解所必需的信息。

多段图、矩阵连乘问题题目

凸多边形最优三角剖分

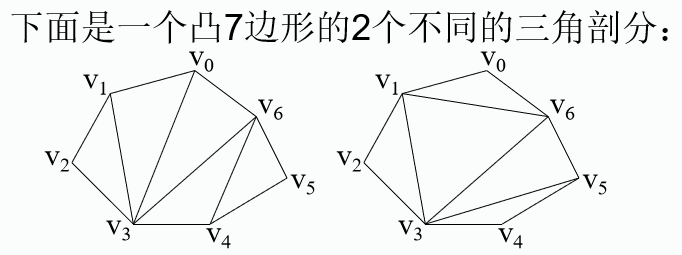
凸多边形的最优三角剖分问题：给定凸多边形P={v0, v1,…, vn–1} （注意最后一个节点的标号为n-1），以及定义在由凸多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的一个三角剖分，使得该剖分中诸三角形上权之和为最小。

可定义三角形上各种各样的权函数w。

例如

，其中|vivj|是点vi到vj的欧氏距离。相应于此权函数的最优三角剖分即为最小弦长三角剖分。

三角剖分与矩阵连乘积同构

三角剖分问题和矩阵连乘积问题都对应于一个完全二叉树，也称为表达式的语法树。

n个矩阵连乘积计算顺序同构于n个叶子的完全二叉树，凸(n+1)边形三角剖分同构于n个叶子的完全二叉树，所以n个矩阵连乘积的计算顺序问题同构于凸(n+1)边形的三角剖分问题。

事实上，矩阵连乘积最优计算顺序问题相当于是凸多边形最优三角剖分问题中一种特殊定义的权函数的情形。

证明：凸多边形剖分具有最优子结构？

能应用动态规划求解的问题应具有最优子结构性质。凸多边形最优三角剖分问题具有最优子结构性质。

事实上，若凸(n+1)边形P={v0, v1,…, vn}的一个最优三角剖分T包含了三角形v0vkvn，1≤k＜n，则T的权为三角形v0vkvn、多边形{v0, v1,…, vk} 和多边形{vk, vk+1,…, vn}的权之和。显然这两个子多边形的三角剖分也是最优的。

因为，其中若有一个子多边形的三角剖分不是最优的将导致T不是最优三角剖分的矛盾。

最优三角剖分的递归结构

定义t[i][j]（注意第一个参数为子多边形的第二个顶点）, 1≤i<j≤n, 为子多边形{vi–1, vi,…, vj}的最优三角剖分所对应的权函数值，并为方便起见，设退化的多边形{vi–1, vi}的权值为0。

于是凸(n+1)边形的最优三角剖分为t[1][n]

易知，t[i][j]可递归定义为当i = j时，为退化多边形{vi–1, vi}，t[i][j] = 0；当i＜j时，利用最优子结构性质有：

与矩阵连乘积问题相对比：

显然，矩阵连乘积的最优计算顺序与凸多边形最优三角剖分具有完全相同的递归结构。

最优三角剖分的算法

由于凸多边形最优三角剖分与矩阵连乘积的最优计算顺序具有完全相同的递归结构，其区别仅在于权函数的不同，所以只需要修改求矩阵连乘积的最优计算顺序的算法中的权函数计算便可得到凸多边形最优三角剖分的算法。显然该算法的时间复杂性也是O(n3)。

最长公共子序列

A,B的长度最大公共子序列称为A,B的最长公共子序列。

例如：A=<a,b,c,b,d,a,c,b>，B=<b,d,c,a,b>，C1=<b,a,b>是A、B的一个公共子序列，但不是最长子序列。C2=<b,d,a,b>和C3=<b,c,a,b>都是A、B的最长子序列。

注意：这里的子序列对于原序列而言不一定是连续的。

求最长公共子序列

对

求序列A、B的最长公共子序列的最直接方法是对A的所有子序列逐个检查是否为B的子序列，并且在检查过程中记录最长子序列。

A的每个子序列对应下标集{1,2,...n}的一个子集，因此遍历所有A的不同子序列要求的时间复杂性为O(2n)。显然这不是一个有效的方法。

最长公共子序列性质

如果C=<c1,c2,…,cr>是A、B的一个最长公共子序列，则C必为如下三种情况之一：

1） 如果an=bm，则cr= an=bm ，即Cr-1是An-1和Bm-1的最长公共子序列；
（A的最后一个字符和B的最后一个字符相同，那么他们的最长公共子序列的最后一个字符就是这个字符，可以退出C出去最后一个字符是A除去最后一个字符和B除去最后一个字符的最长公共子序列）

2） 如果an≠bm且cr ≠an，则C是An-1和B的最长公共子序列；
（A和B的最后一个字符不同，那么C的最后一个字符不是A的最后一个字符，可以C是A除去最后一个字符和B的最长公共子序列）

3） 如果an≠bm且cr ≠bm，则C是A和Bm-1的最长公共子序列；

即两个序列的最长公共子序列包含了这两个序列前缀的最长公共子序列。

最长公共子序列的递归结构

计算A、B的最长公共子序列可能要求计算A、Bm-1的公共最长子序列或者An-1、B的公共最长子序列，而这两个子问题又都包含求An-1、Bm-1的公共最长子序列。

求最长公共子串长度的算法

也就是最后一位相同，那么这个值=左上角的数加一(flag=0)。如果最后一位不相同，那么这个值=max{上边的值(flag=-1)，左面的值（flag=1）}

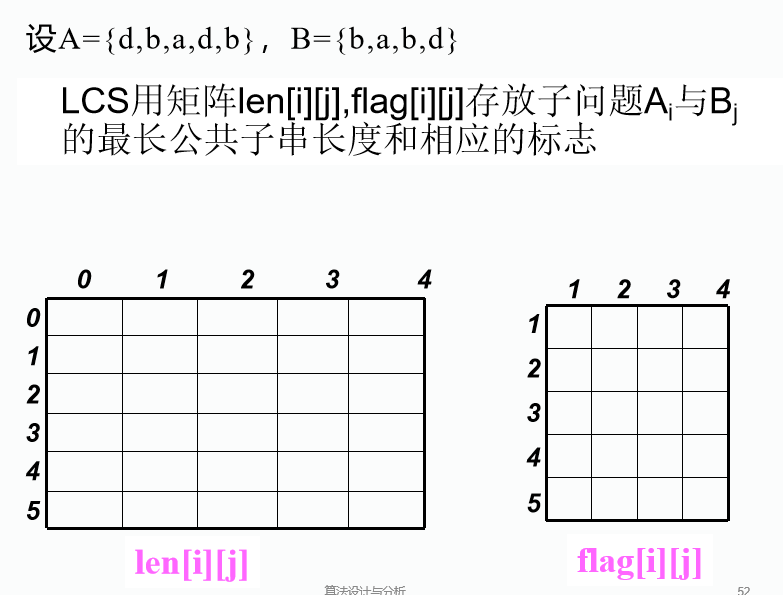
初始化

结果

最长公共子序列的长度=len[i][j]右下角的值

LCS的时间复杂性

算法LCSlength的主要计算取决于程序中对i和j的二重循环，循环的总次数为O(nm)。算法LCS0的每次递归调用中i减1或者j减1，因此时间复杂性为O(n+m)。

动态规划总结

与分治法相比，相同之处是也将原问题分解为若干子问题，再递归求解；不同之处是所分解的子问题彼此并不独立，而是互有重叠。

基本思想是造表记录已解的子问题，再次遇到时仅查表即可，避免了重复计算，提高效率。

通常用于求解具有最优性质的问题，而且其子问题也具有最优性质(最优子结构性质)。

实现方法通常为自底向上的递归形式，但也可以采用自上而下的形式(备忘录方法)。