leetcode刷题记录07（2023-04-30）【二叉树展开为链表 | 买卖股票的最佳时机 | 二叉树中的最大路径和(递归) | 最长连续序列(并查集)】

114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

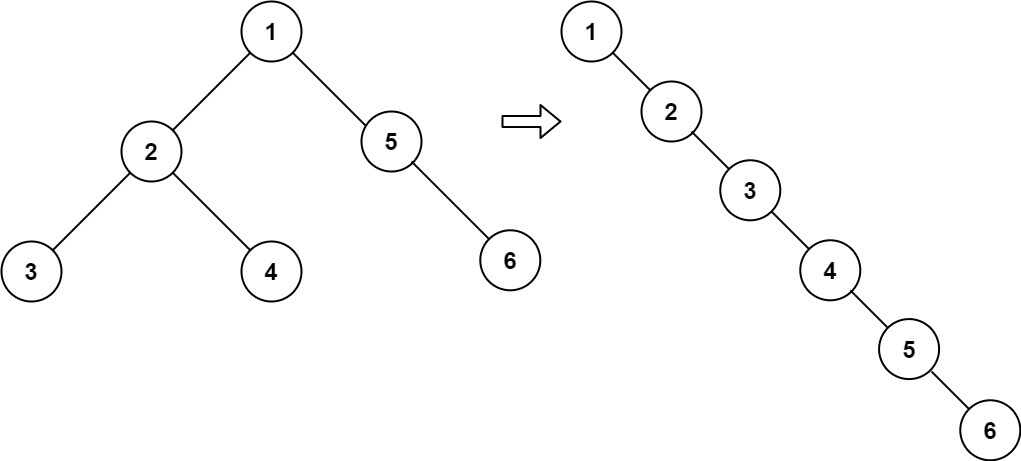
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [0]
输出：[0]

提示：
$树中结点数在范围[0,2000]内$
$?100<=Node.val<=100$

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

现在刷leetcode经常一遍就可以通过，代码不需要调试，感觉还是很有成就感的，刷题确实有效果。

这道题目如果不要求使用原地算法（O(1) 额外空间），很简单，进行前序遍历，保存数组的指针到数组中，最后再进行一次树的重建，但是复杂度是O(n)。

或者采用一个栈的数据结构，保存一下右子树，不断地进行前序遍历，将当前节点添加到 pre->right 中，pre->left 中填写 nullptr。

值得注意的是，需要对空子树进行处理，如果 root 节点为空，直接返回。

代码如下：

#include<stack>
using namespace std;

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
 
class Solution {
public:
    void flatten(TreeNode* root) {
        if (root == nullptr) {
            return;
        }
        stack<TreeNode*> stk;
        if (root->right != nullptr) {
            stk.push(root->right);
        }
        // 前驱节点
        TreeNode* pre = root;
        // 当前节点
        TreeNode* cur = root->left;
        while (!stk.empty() || cur != nullptr) {
            if (cur == nullptr) {
                cur = stk.top();
                stk.pop();
            }
            // 将右节点入栈
            if (cur->right != nullptr) {
                stk.push(cur->right);
            }
            // pre->right
            pre->right = cur;
            pre->left = nullptr;
            pre = pre->right;
            // 更新 cur
            cur = cur->left;
        }
    }
};

虽然采用栈降低了空间复杂度，但是也并不能说是O(1)级别的，看了下题解，思路是：对于每个节点，每次将它的左节点变为空，然后就移动到它的右节点上去。主要是找到左子树中最后一个访问的节点，将右子树移到它上面，最后再将左子树整体移动到 root->right 上。

代码如下：

class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode *curr = root;
        while (curr != nullptr) {
            if (curr->left != nullptr) {
                auto next = curr->left;
                auto predecessor = next;
                while (predecessor->right != nullptr) {
                    predecessor = predecessor->right;
                }
                predecessor->right = curr->right;
                curr->left = nullptr;
                curr->right = next;
            }
            curr = curr->right;
        }
    }
};

121. 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：
输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：
$1<=prices.length<=10^5$
$0<=prices[i]<=10^4$

还是一遍过！

主要思路就是从前向后进行遍历，保存最小值，然后用当前值-最小值，如果大于当前的最大利润，就更新最大利润。最后返回最大利润。

代码如下：

#include<vector>
using namespace std;

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int minVal = 0x3f3f3f3f;
        int profit = 0;
        for (int i = 0; i < prices.size(); i++) {
            if (prices[i] < minVal)minVal = prices[i];
            profit = profit > (prices[i] - minVal) ? profit : (prices[i] - minVal);
        }
        return profit;
    }
};

124. 二叉树中的最大路径和

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

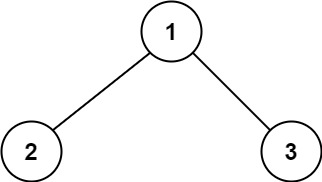
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

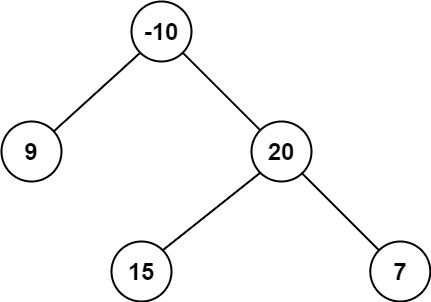
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：
$树中节点数目范围是[1,3?10^4]$
$?1000<=Node.val<=1000$

很优美的代码，主要通过一个共享成员变量记录全局最优解，再 maxGain 内部有进行局部最优解的计算，并不断更新全局最优解。

同时，maxGain 的返回值，返回的是当前节点作为路径的一部分，要么要左子树，要么要右子树，不能两个都要(这样才能保证 同一个节点在一条路径序列中至多出现一次 )。

#include<algorithm>

using namespace std;

//  Definition for a binary tree node.
 struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  };
 
class Solution {
    int maxSum = -0x3f3f3f3f - 1;

    int maxGain(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }

        int leftGain = max(maxGain(root->left), 0);
        int rightGain = max(maxGain(root->right), 0);

        int curMax = root->val + leftGain + rightGain;

        maxSum = max(maxSum, curMax);

        return root->val + max(leftGain, rightGain);
    }

public:
    int maxPathSum(TreeNode* root) {
        maxGain(root);
        return maxSum;
    }
};

128. 最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：
输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：
输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

提示：

$0<=nums.length<=10^5$
$?10^9<=nums[i]<=10^9$

主要思路就是采用并查集来实现，首先要去重，得到一个哈希表，然后遍历这个哈希，如果存在连续的数，那么就需要进行合并，合并的时候要将大的数作为根，这样我们就将所有连续的数划分在一个集合里面了。

最后遍历一遍哈希表，判断当前元素是否为序列的第一个数。

• 如果是第一个数，则找到它的祖先，根据祖先的值，就可以确定序列的长度。
• 如果不是第一个数，不考虑。

#include<vector>
#include<unordered_map>
using namespace std;

class Solution {
    vector<int> mergeAndFindSet;
    int find(int val) {
        while (mergeAndFindSet[val] != val)
        {
            val = mergeAndFindSet[val];
        }
        return val;
    }

    void merge(int val1, int val2) {
        int i1 = find(val1);
        int i2 = find(val2);
        // 找到 i1 和 i2 后进行合并
        if (i1 == i2) return;
        mergeAndFindSet[i1] = i2;
    }
public:
    int longestConsecutive(vector<int>& nums) {
        

        unordered_map<int, int> mp;
        int n = nums.size();

        mergeAndFindSet = vector<int>(n, 0);
        for (int i = 0; i < n; i++) {
            mergeAndFindSet[i] = i;
        }
        for (int i = 0; i < n; i++) {
            mp[nums[i]] = i;
        }

        for (auto it = mp.begin(); it != mp.end(); it++) {
            int num = it->first;
            int i = it->second;
            if (mp.count(num + 1)) {        // 如果有连续的数就进行合并
                merge(i, mp[num + 1]);    // 合并需要将小的数合并到最大的根上
            }
        }

        int res = 0;
        for (auto it = mp.begin(); it != mp.end(); it++) {
            int num = it->first;
            int i = it->second;
            if (!mp.count(num - 1)) { // 如果当前这个数是最小的，寻找它的根
                int root = find(i);
                res = max(res, nums[root] - num + 1);
            }
        }
        return res;
    }
};