Python | 使用VIF检测多重共线性
2023-12-25 20:42:04
多重共线性是指多元回归模型中有两个或两个以上的自变量,它们之间具有高度的相关性。当某些特征高度相关时,我们可能很难区分它们对因变量的个体影响。多重共线性可以使用各种技术来检测,其中一种技术是方差膨胀因子(VIF)。
在VIF方法中,我们选择每个特征并将其与所有其他特征进行回归。对于每个回归,因子计算如下:
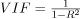
其中,R平方是线性回归中的决定系数。它的值介于0和1之间。
正如我们从公式中看到的,R平方的值越大,VIF越大。因此,VIF越大,相关性越强。这与较高的R平方值表示较强的共线性的事实一致。通常,VIF高于5表示高多重共线性。
使用statmodels实现VIF:
statsmodels提供了一个名为variance_inflation_factor()的函数来计算VIF。
语法:statmodels.stats.outliers_influence.variance_inflation_factor(exog,exog_idx)
主要参数:
exog:一个数组,包含对其执行线性回归的特征。
exog_idx:要测量其对其他特征的影响的附加特征的索引。
示例:
下例中使用的数据集包含500人的身高、体重、性别和体重指数。这里的因变量是指数。
import pandas as pd
# the dataset
data = pd.read_csv('BMI.csv')
# printing first few rows
print(data.head())
输出
Gender Height Weight Index
0 Male 174 96 4
1 Male 189 87 2
2 Female 185 110 4
3 Female 195 104 3
4 Male 149 61 3
方法:
- 每个特征索引都被传递给variance_inflation_factor()以找到相应的VIF。
- 这些值以Pandas DataFrame的形式存储。
from statsmodels.stats.outliers_influence import variance_inflation_factor
# creating dummies for gender
data['Gender'] = data['Gender'].map({'Male':0, 'Female':1})
# the independent variables set
X = data[['Gender', 'Height', 'Weight']]
# VIF dataframe
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
# calculating VIF for each feature
vif_data["VIF"] = [variance_inflation_factor(X.values, i)
for i in range(len(X.columns))]
print(vif_data)
输出
feature VIF
0 Gender 2.028864
1 Height 11.623103
2 Weight 10.688377
正如我们所看到的,身高和体重具有非常高的VIF值,表明这两个变量高度相关。这是预料之中的,因为一个人的身高确实会影响他们的体重。因此,将这两个特征一起考虑会导致具有高多重共线性的模型。
文章来源:https://blog.csdn.net/qq_42034590/article/details/134364292
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!