【PyTorch】卷积神经网络
2023-12-14 15:31:08
1. 理论介绍
1.1. 从全连接层到卷积层
1.1.1. 背景
- 使用多层感知机学习图像数据面临参数量巨大、数据量要求高的问题,因此这种缺少结构的网络可能会变得不实用。
- 利用相近像素之间的相互关联性,可以从图像数据中学习得到有效的模型。
- 设计适合于计算机视觉的神经网络架构的原则
- 平移不变性:不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应。
- 局部性:神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系。
1.1.2. 从全连接层推导出卷积层
- 假设多层感知机的输入是二维图像
X
\mathbf{X}
X,隐藏表示为二维张量
H
\mathbf{H}
H,且
X
\mathbf{X}
X和
H
\mathbf{H}
H具有相同的形状,
[
X
]
i
,
j
[\mathbf{X}]_{i,j}
[X]i,j?和
[
H
]
i
,
j
[\mathbf{H}]_{i,j}
[H]i,j?分别表示输入图像和隐藏表示中位置
(
i
,
j
)
(i,j)
(i,j)处的像素。为了使每个隐藏神经元都能接收到每个输入像素的信息,我们将参数从权重矩阵替换为四维权重张量
W
\mathbf{W}
W,偏置为
U
\mathbf{U}
U,则全连接层可表示为
[ H ] i , j = [ U ] i , j + ∑ k ∑ l [ W ] i , j , k , l [ X ] k , l = [ U ] i , j + ∑ a ∑ b [ V ] i , j , a , b [ X ] i + a , j + b \begin{aligned} [\mathbf{H}]_{i,j} &=[\mathbf{U}]_{i,j}+\sum_k\sum_l{[\mathbf{W}]_{i,j,k,l}}{[\mathbf{X}]_{k,l}} \\ &=[\mathbf{U}]_{i,j}+\sum_a\sum_b{[\mathbf{V}]_{i,j,a,b}}{[\mathbf{X}]_{i+a,j+b}} \end{aligned} [H]i,j??=[U]i,j?+k∑?l∑?[W]i,j,k,l?[X]k,l?=[U]i,j?+a∑?b∑?[V]i,j,a,b?[X]i+a,j+b??
其中, [ V ] i , j , a , b = [ W ] i , j , i + a , j + b [\mathbf{V}]_{i,j,a,b}=[\mathbf{W}]_{i,j,i+a,j+b} [V]i,j,a,b?=[W]i,j,i+a,j+b?,索引 a a a和 b b b通过在正偏移和负偏移之间移动覆盖了整个图像。 - 平移不变性意味着检测对象在输入
X
\mathbf{X}
X中的平移,应该仅导致隐藏表示
H
\mathbf{H}
H中的平移,即
U
\mathbf{U}
U和
V
\mathbf{V}
V不依赖与
(
i
,
j
)
(i,j)
(i,j)的值,则有
{ [ V ] i , j , a , b = [ V ] a , b [ U ] i , j = u \begin{cases} [\mathbf{V}]_{i,j,a,b} &= [\mathbf{V}]_{a,b}\\ [\mathbf{U}]_{i,j}&=u \end{cases} {[V]i,j,a,b?[U]i,j??=[V]a,b?=u?
因而我们可以简化 H \mathbf{H} H的定义为
[ H ] i , j = u + ∑ a ∑ b [ V ] a , b [ X ] i + a , j + b [\mathbf{H}]_{i,j} = u + \sum_a\sum_b{[\mathbf{V}]_{a,b}}{[\mathbf{X}]_{i+a,j+b}} [H]i,j?=u+a∑?b∑?[V]a,b?[X]i+a,j+b? - 局部性意味着当
∣
a
∣
>
Δ
|a|>\Delta
∣a∣>Δ或
∣
b
∣
>
Δ
|b|>\Delta
∣b∣>Δ时,
[
V
]
a
,
b
=
0
[\mathbf{V}]_{a,b}=0
[V]a,b?=0,因而我们可以得到
[ H ] i , j = u + ∑ a = ? Δ Δ ∑ b = ? Δ Δ [ V ] a , b [ X ] i + a , j + b [\mathbf{H}]_{i,j} = u + \sum_{a=-\Delta}^{\Delta}\sum_{b=-\Delta}^{\Delta}{[\mathbf{V}]_{a,b}}{[\mathbf{X}]_{i+a,j+b}} [H]i,j?=u+a=?Δ∑Δ?b=?Δ∑Δ?[V]a,b?[X]i+a,j+b?
上式就是一个卷积层,其中 V \mathbf{V} V被称为卷积核或卷积层的权重,而卷积神经网络是包含卷积层的一类特殊的神经网络。 - 卷积神经网络相较于多层感知机,参数大幅减小,但代价是图像特征要求是平移不变的,并且当确定每个隐藏神经元激活值时,每一层只包含局部的信息。
1.2. 卷积层
1.2.1. 图像卷积
- 卷积运算
- 数学定义: ( f ? g ) ( x ) = ∫ f ( z ) g ( x ? z ) d z (f * g)(\mathbf{x}) = \int f(\mathbf{z}) g(\mathbf{x}-\mathbf{z}) d\mathbf{z} (f?g)(x)=∫f(z)g(x?z)dz
- 针对一维离散对象: ( f ? g ) ( i ) = ∑ a f ( a ) g ( i ? a ) (f * g)(i) = \sum_a f(a) g(i-a) (f?g)(i)=a∑?f(a)g(i?a)
- 针对二维离散对象: ( f ? g ) ( i , j ) = ∑ a ∑ b f ( a , b ) g ( i ? a , j ? b ) (f * g)(i, j) = \sum_a\sum_b f(a, b) g(i-a, j-b) (f?g)(i,j)=a∑?b∑?f(a,b)g(i?a,j?b)
- 上述卷积层所描述的运算使用 ( i + a , j + b ) (i+a,j+b) (i+a,j+b),称为互相关运算,但这种与卷积运算使用 ( i ? a , j ? b ) (i-a,j-b) (i?a,j?b)的实质是一致的,因为我们总是可以匹配两种运算之间的符号。
- 在卷积层中,输入张量和核张量通过互相关运算产生输出张量。具体过程是卷积核窗口从输入张量的左上角开始,从左到右、从上到下滑动。 当卷积核窗口滑动到新一个位置时,包含在该窗口中的部分张量与卷积核张量进行按元素相乘,得到的张量再求和得到一个单一的标量值,由此我们得出了这一位置的输出张量值。
- 卷积层中的两个被训练的参数是卷积核权重和标量偏置。
- 要执行严格卷积运算,我们只需水平和垂直翻转二维卷积核张量,然后对输入张量执行互相关运算。由于卷积核是从数据中学习到的,因此无论这些层执行严格的卷积运算还是互相关运算,卷积层的输出都不会受到影响,以后不加区别统称卷积运算。
- 由于输入图像是三维的,对于每一个空间位置,我们想要采用一组而不是一个隐藏表示。这样一组隐藏表示可以想象成一些互相堆叠的二维网格。 因此,我们可以把隐藏表示想象为一系列具有二维张量的通道(channel)。这些通道有时也被称为特征映射(feature maps),因为每个通道都向后续层提供一组空间化的学习特征,可以被视为输入映射到下一层的空间维度的转换器。
- 在卷积神经网络中,对于某一层的任意元素 x x x,其感受野(receptive field)是指在前向传播期间可能影响 x x x计算的所有元素(来自所有先前层)。当需要检测输入特征中更广区域时,我们可以构建一个更深的卷积网络。
1.2.2. 填充和步幅
- 卷积的输出形状取决于输入形状和卷积核的形状。
- 在应用多层卷积时,我们常常丢失边缘像素。解决这个问题的简单方法即为填充(padding),即在输入图像的边界填充元素(通常填充元素是0)。
- 一般在顶部和底部填充相同数量的行,在左侧和右侧填充相同数量的列。
- 输入 n h × n w n_h\times n_w nh?×nw?,卷积核 k h × k w k_h\times k_w kh?×kw?,上下分别填充 p h p_h ph?行,左右分别填充 p w p_w pw?列,则输出 ( n h ? k h + 1 + 2 ? p h ) × ( n w ? k w + 1 + 2 ? p w ) (n_h-k_h+1+2*p_h)\times(n_w-k_w+1+2*p_w) (nh??kh?+1+2?ph?)×(nw??kw?+1+2?pw?)
- 在许多情况下,我们需要设置 p h = ( k h ? 1 ) / 2 p_h=(k_h-1)/2 ph?=(kh??1)/2和 p w = ( k w ? 1 ) / 2 p_w=(k_w-1)/2 pw?=(kw??1)/2,使输入和输出具有相同的高度和宽度,这样可以在构建网络时更容易地预测每个图层的输出形状。
- 当卷积核的高度和宽度不同时,我们可以填充不同的高度和宽度,使输出和输入具有相同的高度和宽度。
- 有时候为了高效计算或是缩减采样次数,卷积窗口可以跳过中间位置,每次滑动多个元素,每次滑动元素的数量称为步幅(stride)。
- 输入 n h × n w n_h\times n_w nh?×nw?,卷积核 k h × k w k_h\times k_w kh?×kw?,上下分别填充 p h p_h ph?行,左右分别填充 p w p_w pw?列,垂直步幅为 s h s_h sh?,水平步幅为 s w s_w sw?,则输出 ? ( n h ? k h + 2 ? p h + s h ) / s h ? × ? ( n w ? k w + 2 ? p w + s w ) / s w ? \lfloor(n_h-k_h+2*p_h+s_h)/s_h\rfloor\times\lfloor(n_w-k_w+2*p_w+s_w)/s_w\rfloor ?(nh??kh?+2?ph?+sh?)/sh??×?(nw??kw?+2?pw?+sw?)/sw??如果我们设置了 p h = ( k h ? 1 ) / 2 p_h=(k_h-1)/2 ph?=(kh??1)/2和 p w = ( k w ? 1 ) / 2 p_w=(k_w-1)/2 pw?=(kw??1)/2,则输出 ? ( n h + s h ? 1 ) / s h ? × ? ( n w + s w ? 1 ) / s w ? \lfloor(n_h+s_h-1)/s_h\rfloor\times\lfloor(n_w+s_w-1)/s_w\rfloor ?(nh?+sh??1)/sh??×?(nw?+sw??1)/sw??如果进一步,输入的高度和宽度可以被垂直和水平步幅整除,则输出 ( n h / s h ) × ( n w / s w ) (n_h/s_h)\times(n_w/s_w) (nh?/sh?)×(nw?/sw?)
- 为了简洁起见,输入高度上下两侧分别为 p h p_h ph?,输入宽度左右两侧的填充数量分别为 p w p_w pw?时,称为填充 ( p h , p w ) (p_h,p_w) (ph?,pw?), p h = p w = p p_h=p_w=p ph?=pw?=p时,填充是 p p p;同理,高度和宽度上的步幅分别为 s h s_h sh?和 s w s_w sw?时,称为步幅 ( s h , s w ) (s_h,s_w) (sh?,sw?), s h = s w = s s_h=s_w=s sh?=sw?=s时,步幅是 s s s。默认情况下,填充为0,步幅为1。在实践中,我们很少使用不一致的步幅或填充,即总有 p h = p w p_h=p_w ph?=pw?和 s h = s w s_h=s_w sh?=sw?。
1.2.3. 多通道
- 多输入通道
- 假设输入的通道数为 c i c_i ci?,那么卷积核的输入通道数也需要为 c i c_i ci?,如果单通道卷积核的窗口形状是 k h × k w k_h\times k_w kh?×kw?,那么通道数为 c i c_i ci?的卷积核的窗口形状为 c i × k h × k w c_i\times k_h\times k_w ci?×kh?×kw?。
- 多通道输入和多输入通道卷积核之间进行二维互相关运算可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算,再对通道求和得到二维张量。
- 多输出通道
- 可以将每个通道看作对不同特征的响应,但多输出通道并不仅是学习多个单通道的检测器,因为每个通道不是独立学习的,而是为了共同使用而优化的。
- 假设 c i , c o c_i,c_o ci?,co?分别为输入输出通道数, k h , k w k_h,k_w kh?,kw?分别为卷积核的高度和宽度,则为了获得多个通道的输出,我们可以为每个输出通道创建一个形状为 c i × k h × k w c_i\times k_h\times k_w ci?×kh?×kw?的卷积核张量,这样卷积核的形状为 c o × c i × k h × k w c_o\times c_i\times k_h\times k_w co?×ci?×kh?×kw?。在互相关运算中,每个输出通道先获取所有输入通道,再以对应该输出通道的卷积核计算出结果。
-
1
×
1
1\times1
1×1卷积层
- 失去了卷积层的特有能力——在高度和宽度维度上,识别相邻元素间相互作用的能力。
- 唯一计算发生在通道上。输出中的每个元素都是从输入图像中同一位置的元素的线性组合。 可以将 1 × 1 1\times1 1×1卷积看作在每个像素位置应用的全连接层。 1 × 1 1\times1 1×1卷积层的权重维度为 c i × c o c_i\times c_o ci?×co?,再额外加上一个偏置。
- 通常用于调整网络层的通道数量和控制模型复杂性。
1.3. 池化层(又称汇聚层)
1.3.1. 背景
- 机器学习任务通常会跟全局图像的问题有关,所以我们最后一层的神经元应该对整个输入的全局敏感。通过逐渐聚合信息,生成越来越粗糙的映射,最终实现学习全局表示的目标,同时将卷积图层的所有优势保留在中间层。
- 池化层的主要作用是降低卷积层对位置的敏感性,同时降低对空间降采样表示的敏感性。
1.3.2. 池化运算
- 与卷积运算类似, p × q p\times q p×q池化运算使用一个固定形状为 p × q p\times q p×q的池化窗口,根据其步幅大小在输入的所有区域上滑动计算相应输出。
- 池化运算是确定性的,我们通常计算池化窗口中所有元素的最大值或平均值。这些操作分别称为最大池化(maximum pooling)和平均池化(average pooling)。
1.3.3. 填充和步幅
池化层的填充和步幅与卷积层类似。默认情况下,深度学习框架中的步幅与池化窗口的形状大小相同。
1.3.4. 多通道
在处理多通道输入数据时,池化层在每个输入通道上单独运算,而不是像卷积层一样在通道上对输入进行汇总。 这意味着池化层的输出通道数与输入通道数相同。
1.4. 卷积神经网络(LeNet)
1.4.1. 简介
- LeNet是最早发布的卷积神经网络之一,由AT&T贝尔实验室的研究员Yann LeCun在1989年提出的(并以其命名),目的是识别图像中的手写数字。
- Yann LeCun发表了第一篇通过反向传播成功训练卷积神经网络的研究,这项工作代表了十多年来神经网络研究开发的成果。
- LeNet被广泛用于自动取款机(ATM)机中,帮助识别处理支票的数字。
1.4.2. 组成
- 总体来看,LeNet(LeNet-5)由两个部分组成:
- 卷积编码器:由两个卷积层组成;
- 全连接层密集块:由三个全连接层组成。

- 数据维度变化
卷积层数据维度表示:(样本数,通道数,高度,宽度);
展平层、全连接层输出数据维度表示:(样本数,输出数)。位置 数据维度 输入数据 28 x 28 (C1) 5 × 5 5\times5 5×5卷积层(填充2)输入 1 x 1 x 28 x 28 (C1) 5 × 5 5\times5 5×5卷积层(填充2)输出 1 x 6 x 28 x 28 Sigmoid激活函数输出 1 x 6 x 28 x 28 (S2) 2 × 2 2\times2 2×2平均池化层(步幅2)输出 1 x 6 x 14 x 14 (C3) 5 × 5 5\times5 5×5卷积层输入 1 x 6 x 10 x 10 (C3) 5 × 5 5\times5 5×5卷积层输出 1 x 16 x 10 x 10 Sigmoid激活函数输出 1 x 16 x 10 x 10 (S4) 2 × 2 2\times2 2×2平均池化层输出 1 x 16 x 5 x 5 展平层输出 1 x 400 (120-F5)全连接层输出 1 x 120 Sigmoid激活函数输出 1 x 120 (84-F6)全连接层输出 1 x 84 Sigmoid激活函数输出 1 x 84 输出结果 1 x 10
2. 实例解析
2.1. 实例描述
- 图像中目标的边缘检测
构造一个 6 × 8 6\times8 6×8像素的黑白图像,中间四列为黑色(0),其余像素为白色(1)。要求进行边缘检测,输出中的1代表从白色到黑色的边缘,-1代表从黑色到白色的边缘,其他情况的输出为0。 - 在FashionMNIST数据集上训练LeNet
2.2. 代码实现
2.2.1. 图像中目标的边缘检测
2.2.1.1. 主要代码
net = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
2.2.1.2. 完整代码
import torch
from torch import nn
from torch.nn import functional as F
if __name__ == '__main__':
# 全局参数设置
lr = 3e-2
num_epochs = 10
# 生成数据集
X = torch.ones(6, 8)
X[:, 2:6] = 0
Y = torch.zeros(6, 7)
Y[:, 1], Y[:, 5] = 1, -1
# 批数、通道数、高度、宽度
X = X.reshape(1, 1, 6, 8)
Y = Y.reshape(1, 1, 6, 7)
print('1. 使用边缘检测器(1, -1)')
K = torch.tensor([1.0, -1.0]).reshape(1, 1, 1, 2)
O = F.conv2d(X, K, bias=None)
print(f'边缘检测器的结果O与标准结果Y是否相同:{O.equal(Y)}')
print('2. 学习卷积核')
net = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
# 训练循环
for epoch in range(num_epochs):
loss = (net(X) - Y) ** 2 # 平方误差
net.zero_grad()
loss.sum().backward()
net.weight.data[:] -= lr * net.weight.grad # 参数更新
print(f'epoch {epoch + 1}, loss {loss.sum():.3f}')
print(f'卷积核权重:{net.weight.data.reshape(1, 2)}')
2.2.1.3. 输出结果
1. 使用边缘检测器(1, -1)
边缘检测器的结果O与标准结果Y是否相同:True
2. 学习卷积核
epoch 1, loss 10.272
epoch 2, loss 4.320
epoch 3, loss 1.842
epoch 4, loss 0.801
epoch 5, loss 0.358
epoch 6, loss 0.165
epoch 7, loss 0.080
epoch 8, loss 0.040
epoch 9, loss 0.022
epoch 10, loss 0.012
卷积核权重:tensor([[ 0.9799, -0.9993]])
2.2.2. 在FashionMNIST数据集上训练LeNet
2.2.2.1. 主要代码
LeNet = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(400, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10)
).to(device)
2.2.2.2. 完整代码
import torch, os
from torch import nn, optim
from torch.utils.data import DataLoader
from torchvision.transforms import Compose, ToTensor, Resize
from torchvision.datasets import FashionMNIST
from tensorboardX import SummaryWriter
from rich.progress import track
def load_dataset():
"""加载数据集"""
root = "./dataset"
transform = Compose([ToTensor()])
mnist_train = FashionMNIST(root, True, transform, download=True)
mnist_test = FashionMNIST(root, False, transform, download=True)
dataloader_train = DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=num_workers,
)
dataloader_test = DataLoader(mnist_test, batch_size, shuffle=False,
num_workers=num_workers,
)
return dataloader_train, dataloader_test
if __name__ == "__main__":
# 全局参数设置
num_epochs = 100
batch_size = 256
num_workers = 3
lr = 0.9
device = torch.device('cuda')
# 创建记录器
def log_dir():
root = "runs"
if not os.path.exists(root):
os.mkdir(root)
order = len(os.listdir(root)) + 1
return f'{root}/exp{order}'
writer = SummaryWriter(log_dir=log_dir())
# 数据集配置
dataloader_train, dataloader_test = load_dataset()
# 模型配置
LeNet = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(400, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10)
).to(device)
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
LeNet.apply(init_weights)
criterion = nn.CrossEntropyLoss(reduction='none')
optimizer = optim.SGD(LeNet.parameters(), lr=lr)
# 训练循环
for epoch in track(range(num_epochs), description='LeNet'):
LeNet.train()
for X, y in dataloader_train:
X, y = X.to(device), y.to(device)
optimizer.zero_grad()
loss = criterion(LeNet(X), y)
loss.mean().backward()
optimizer.step()
LeNet.eval()
with torch.no_grad():
train_loss, train_acc, num_samples = 0.0, 0.0, 0
for X, y in dataloader_train:
X, y = X.to(device), y.to(device)
y_hat = LeNet(X)
loss = criterion(y_hat, y)
train_loss += loss.sum()
train_acc += (y_hat.argmax(dim=1) == y).sum()
num_samples += y.numel()
train_loss /= num_samples
train_acc /= num_samples
test_acc, num_samples = 0.0, 0
for X, y in dataloader_test:
X, y = X.to(device), y.to(device)
y_hat = LeNet(X)
test_acc += (y_hat.argmax(dim=1) == y).sum()
num_samples += y.numel()
test_acc /= num_samples
writer.add_scalars('metrics', {
'train_loss': train_loss,
'train_acc': train_acc,
'test_acc': test_acc
}, epoch)
writer.close()
2.2.2.3. 输出结果
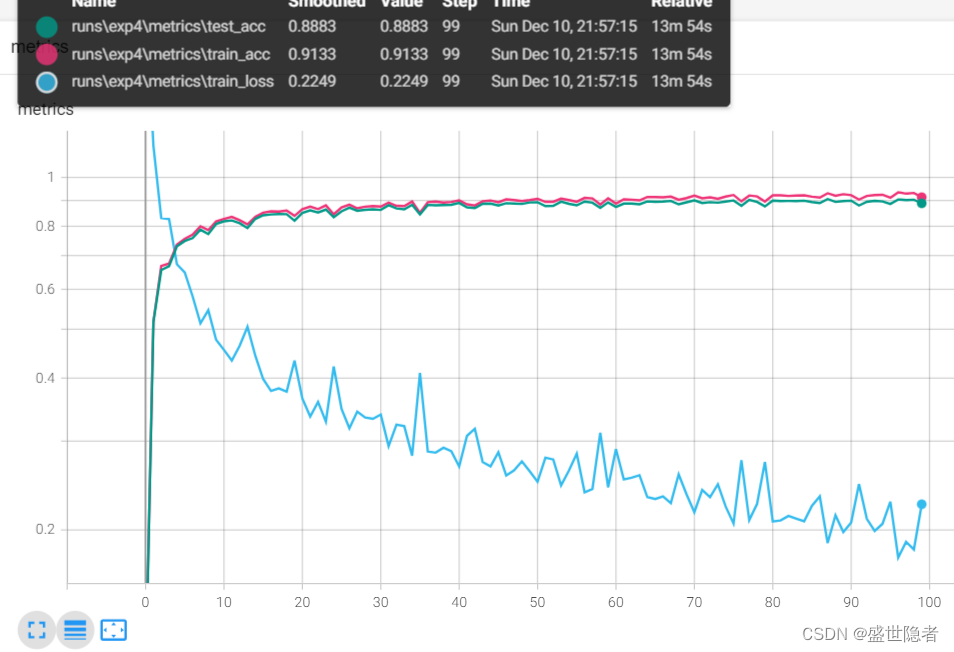
文章来源:https://blog.csdn.net/weixin_45725295/article/details/134901398
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!