ZKP Sigma Protocol

2023-12-26 23:41:52

Sigma Protocol

Introduction

Sigma protocols are a specific type of interactive zero-knowledge proof (ZKP) that are known for their efficiency and simplicity.
They involve three distinct phases between a prover and a verifier:

  • Prover: P ( x , y ) P(x,y) P(x,y)
  • Verifier: V ( y ) V(y) V(y)
  • Commitment: The prover sends an initial commitment t t t to the verifier, often involving a secret value.
  • Challenge: The verifier responds with a random challenge c c c.
  • Response: The prover calculates a response z z z based on the challenge and their secret knowledge and sends it to the verifier.
  • Evaluation: Upon receiving prover’s response z z z, the verifier outputs either accept or reject, which must be computed strictly as a function of the statement y y y and the conversation ( t , c , z ) (t,c,z) (t,c,z). In particular, the verifier does not make any random choices other than the selection of the challenge: all other computations are completely deterministic.

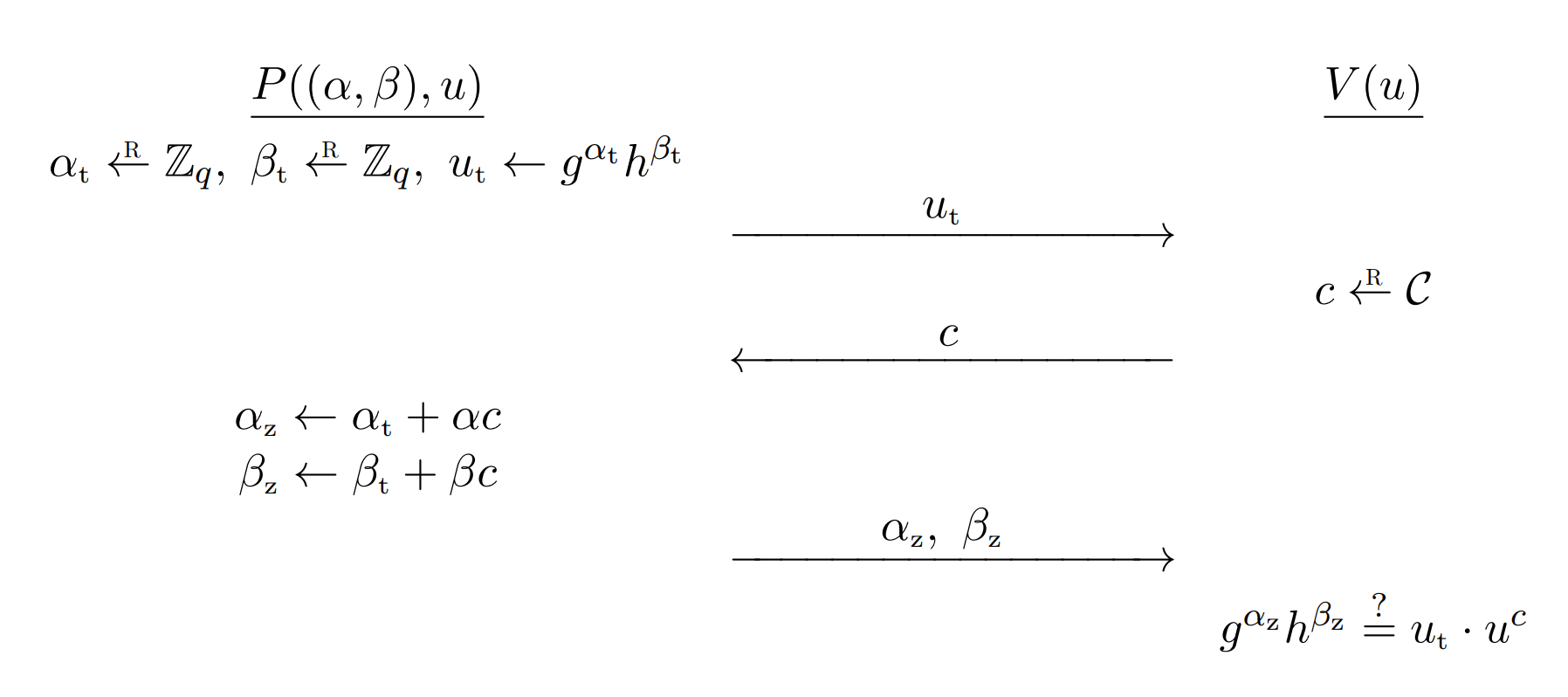
Example: Okamoto’s protocol

Okamoto’s protocol allows a prover to convince a skeptical verifier that he “knows” a representation of a given u ∈ G u \in \mathbb{G} u∈G, without revealing anything about that representation to the verifier.

A witness for the statement u ∈ G u \in \mathbb{G} u∈G is ( α ; β ) ∈ Z q 2 (\alpha; \beta) \in \mathbb{Z}_q^2 (α;β)∈Zq2?such that g α h β = u g^{\alpha}h^{\beta} = u gαhβ=u, i.e., a representation of u u u. Thus, in this example, every statement has many witnesses.

  • Prover: P ( ( α , β ) , u ) P((\alpha, \beta), u) P((α,β),u)
  • Verifier: V ( u ) V(u) V(u)
  • The prover computes α t ← G \alpha_t \leftarrow \mathbb{G} αt?←G, β t ← G \beta_t \leftarrow \mathbb{G} βt?←G, u t ← g α t h β t u_t \leftarrow g^{\alpha_t}h^{\beta_t} ut?←gαt?hβt? and sends the commitment u t u_t ut? to the verifier.
  • The verifier computes a random c c c and sends the challenge c c c to the prover.
  • The prover computes α z ← α t + α c ∈ Z q \alpha_z \leftarrow \alpha_t + \alpha c \in \mathbb{Z}_q αz?←αt?+αc∈Zq?, β z ← β t + β c ∈ Z q \beta_z \leftarrow \beta_t + \beta c \in \mathbb{Z}_q βz?←βt?+βc∈Zq? and sends the response ( α z , β z ) (\alpha_z, \beta_z) (αz?,βz?) to the verifier.
  • The verifier checks if g α z h β z = u t ? u c g^{\alpha_z}h^{\beta_z} = u_t \cdot u^c gαz?hβz?=ut??uc. if so, the verifier outputs “accept”; otherwise, the verifier outputs “reject”.

在这里插入图片描述

文章来源:https://blog.csdn.net/weixin_45347752/article/details/135232867
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。