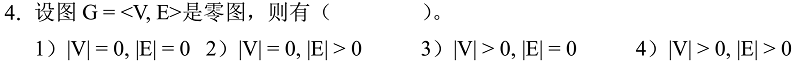【离散数学】——期末刷题题库( 图的基本概念)
🎃个人专栏:
🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客
🐳Java基础:Java基础_IT闫的博客-CSDN博客
🐋c语言:c语言_IT闫的博客-CSDN博客
🐟MySQL:数据结构_IT闫的博客-CSDN博客
🐠数据结构:??????数据结构_IT闫的博客-CSDN博客
💎C++:C++_IT闫的博客-CSDN博客
🥽C51单片机:C51单片机(STC89C516)_IT闫的博客-CSDN博客
💻基于HTML5的网页设计及应用:基于HTML5的网页设计及应用_IT闫的博客-CSDN博客??????
🥏python:python_IT闫的博客-CSDN博客
🐠离散数学:离散数学_IT闫的博客-CSDN博客
欢迎收看,希望对大家有用!
目录
1.?(单选题)若供选择答案中的数值表示一个简单图中各个顶点的度,能画出图的是(??? )
9.?(单选题)有向图D=如下,V1 到V4 长度为2 的通路有( )条。
10.?(单选题)若下列数值表示一个简单图中各顶点的度数序列,含有孤立点的图是(? )。
11.?(单选题)设简单图G所有结点的度数之和为12,则G一定有( )
13.?(单选题)若下列数值表示一个简单图中各顶点的度数序列,可以成连通图的是( )。
18.?(判断题)无向连通图G的任意两结点之间都存在一条路径。
一. 单选题(共14题,70分)
1.?(单选题)若供选择答案中的数值表示一个简单图中各个顶点的度,能画出图的是(??? )
- A. (1,2,5,3,4,5)?
- B. (1,1,3,4,4,5)
- C. (1,1,1,2,2,3)
- D. (2,3,3,4,5,6)
2.?(单选题)
设无向图中有6条边,有一个3度顶点和一个5度顶点,其余顶点度为2,则该图的顶点数是( )
- A. 3
- B. 4
- C. 5
- D. 6
3.?(单选题)
- A. 1
- B. 2
- C. 3
- D. 4
4.?(单选题)
- A. 1
- B. 2
- C. 3
- D. 4
5.?(单选题)
在有n个结点的连通图中,其边数??? (???? )
- A.
最多有n - 1条
- B.
至少有n - 1条
- C.
最多有n条??
- D.
至少有n条
6.?(单选题)
- A. 1
- B. 2
- C. 3
- D. 4
7.?(单选题)
设D=<V,E>为有向图,V={a,b,c,d,e,f},E={<a,b>,<b,c>,<a,d>,<d,e>.<f,e>}是(? ? ?)
- A.
强连通图?
- B.
单向连通图?
- C.
弱连通图?
- D.
不连通图
8.?(单选题)
- A. 1
- B. 2
- C. 3
- D. 4
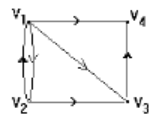
9.?(单选题)有向图D=<V , E>如下,V1 到V4 长度为2 的通路有( )条。
- A. 0
- B. 1
- C. 2
- D. 3
10.?(单选题)若下列数值表示一个简单图中各顶点的度数序列,含有孤立点的图是(? )。
- A. (1,1,2,5,3)?
- B. ?(4,0,4,3,4)
- C. (0,1,1,2)
- D. (1,3,4,4,5)
11.?(单选题)设简单图G所有结点的度数之和为12,则G一定有( )
- A. 3条边
- B. 4条边
- C. 5条边
- D. 6条边
12.?(单选题)
- A. 1
- B. 2
- C. 3
- D. 4
13.?(单选题)若下列数值表示一个简单图中各顶点的度数序列,可以成连通图的是( )。
- A. (1,1,2,5,3)
- B. (4,0,4,3,4)
- C. (0,1,3,3)
- D. (1,3,4,4,5)
14.?(单选题)
- A. 1
- B. 2
- C. 3
- D. 4
二. 多选题(共3题,15分)
15.?(多选题)
- A. 1
- B. 2
- C. 3
- D. 4
- E. 5
答案解析:
16.?(多选题)
- A. 1
- B. 2
- C. 3
- D. 4
- E. 5
17.?(多选题)
- A. 1
- B. 2
- C. 3
- D. 4
- E. 5
三. 判断题(共3题,15分)
18.?(判断题)无向连通图G的任意两结点之间都存在一条路径。
- A. 对
- B. 错
19.?(判断题)
- A. 对
- B. 错
20.?(判断题)
- A. 对
- B. 错
🎯答案:
1-5:CBABB
6-10:ACCBC
11-14:DBAB
15:AD
16:ACE
17:ABE
18-20:对错对
20题答案解析:
集会上,相互认识可以看成是一个等价关系,该题就是证明等价划分中有以下两种情况:1.某划分块中至少有3个元素(同一划分块的人相互认识);2.至少有3个划分块(分属3个划分块的人相互不认识)。
也可以把人看成顶点,认识看成无向边,证明该题有以下两种情况;1.某连通分支中至少有3个点(同一连通分支的人相互认识);2. 至少有3个连通分支(分属不同连通分支的人相互不认识)。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!