机器学习算法(12) — 集成技术（Boosting — Xgboost 分类）

一、说明

????????时间这是集成技术下的第 4 篇文章，如果您想了解有关集成技术的更多信息，您可以参考我的第 1 篇集成技术文章。

二、关于XGBoost

????????XGBoost 是梯度提升的一种更正则化的形式。XGBoost 使用高级正则化（L1 和 L2），提高了模型泛化能力。与梯度提升相比，XGBoost 提供了高性能。它的训练速度非常快，并且可以跨集群并行。

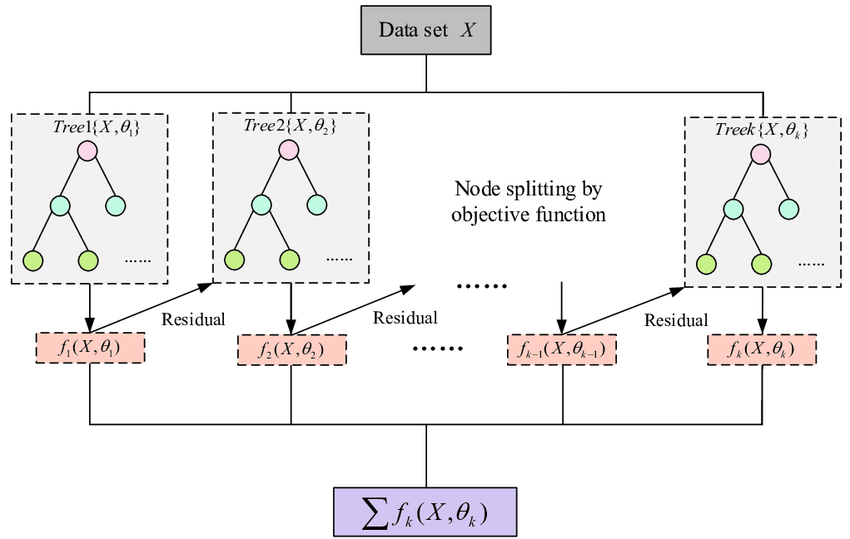
????????XGBoost 通常使用树作为基学习器，该决策树由一系列二元问题组成，最终预测发生在叶子上。XGBoost 本身就是一种集成方法。迭代地构建树，直到满足停止标准。

????????XGBoost 使用CART（分类和回归树）决策树。CART 是在每个叶子中包含实值分数的树，无论它们是用于分类还是回归。如有必要，可以将实值分数转换为类别以进行分类。

2.1 何时使用 XGBoost？

• 当训练样本数量较多时。理想情况下，训练样本大于 1000 个且特征少于 100 个，或者我们可以说特征数量 < 训练样本数量。
• 当存在分类特征和数字特征的混合或仅数字特征时。

2.2 什么时候不应该使用 XGBoost？

• 图像识别
• 计算机视觉
• 当训练样本数量明显小于特征数量时。

????????让我们举一个简单的例子来更好地理解它。银行根据您的工资和信用评分（这是第一、第二和第三个特征）来批准您的信用卡贷款。信用评分分为“不良”、“正常”和“良好”?3 类。由于我们正在解决分类问题，输出 0 或 1。XgBoost 也可用于解决多类分类问题。

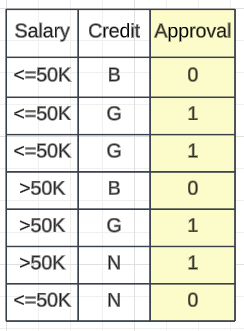
工资贷款审批数据集

三、如何使用Xgboost

3.1 步骤1 -

????????启动XgBoost分类器时，第一步是创建特定的基础模型。在分类问题的情况下，该模型将始终输出 0.5 的概率（输出为零或一）。要计算残差，请从输出值 0.5 中减去实际值。例如，如果批准率为 0.5，则残差将为0–0.5 = -0.5。该基本模型作为所有后续决策树的基础，必须按顺序构建。基本模型本身也是一种决策树，因为它接受输入并提供 0.5 的默认概率。创建基本模型后，下一步就是转向第一个基于顺序的决策树。

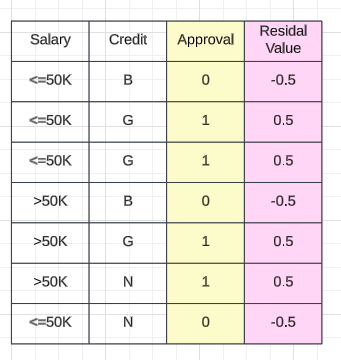
残值

3.2 第2步 -

????????然后，我们使用相关特征创建二元决策树。然后我选择“薪水”作为第一个功能，您有 2 个类别，分别是>50K 和 ≤50K。在XGBoost中，每当你创建一棵树时，你都需要做一个二元分类器。即使您有两个以上类别，这也适用。

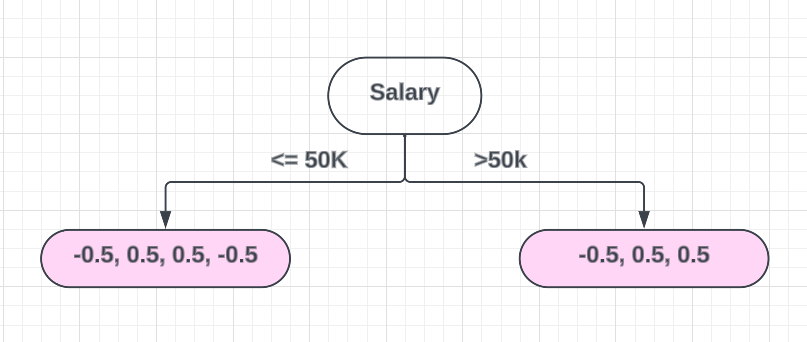
????????为此，您需要创建一个二元分类器并对其进行划分。叶节点始终是两个。然后，根据数据的相似度计算相似度权重，求出Gain。

To come up with these points, we use the values,

≤50K
-0.5, 0.5, 0.5 and -0.5 

>50K
-0.5, 0.5 and 0.5

3.3 步骤 3 —

????????接下来，我们计算相似度权重，其中涉及使用公式，

Similarity Weight = Σ(Residuals) ^2 / Σ(probability * (1 - probability) + λ)

λ= Hyperparameter that prevents overfitting = 0 (For now consider λ value as 0)

probability = This taken from the base model


Similarity Weight of the left leaf node 
------------------------------------
 
Similarity Weight = -0.5 + 0.5 + 0.5 + -0.5 ^ 2/ [0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5)]
Similarity Weight = 0 / 0.25 + 0.25 + 0.25 + 0.25 + 0.25
                  = 0 / 1.25 = 0

Similarity Weight of the right leaf node
------------------------------------
Similarity Weight = -0.5 + 0.5 + 0.5 ^ 2/ [0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5)]
Similarity Weight = 0.5 ^ 2 / 0.75 = 0.25 / 0.75 = 1/3 = 0.33


Similarity Weight of the root node
------------------------------------
Similarity Weight = 0.5 ^ 2/ [0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) ++ 0.5 * (1 - 0.5) ++ 0.5 * (1 - 0.5) ++ 0.5 * (1 - 0.5)]
Similarity Weight = 0.25 / 1.75 = 1/7 = 0.142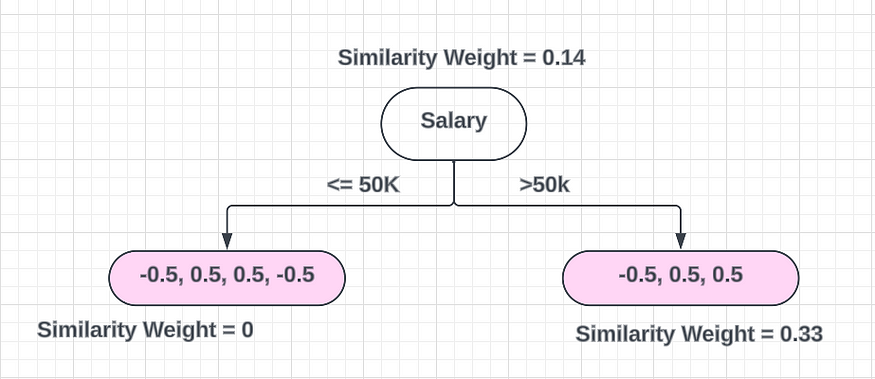

3.4 步骤4-

????????计算信息增益。为此，我们可以将所有叶节点相似性权重加在一起，并从中减去根节点的相似性权重。

Total Gain with respect to the split = 0 + 0.33 - 0.14 = 0.19

????????好的！我们选择了Salary特征进行分割，我们得到的 Gain 为0.19。但我们也可以开始从Credit功能中进行拆分。如果我们开始拆分 Credit 特征，则需要进行二元分类器。叶节点始终是两个。但你有两个以上的类别（“坏”、“正常”和“好”）。为此，您可以像这样进行拆分，

Step 1
=======
Bad
-0.5, -0.5

Good and Normal
0.5, 0.5, 0.5, 0.5 and -0.5

Step 2
==========

Similarity Weight = Σ(Residuals) ^2 / Σ(probability * (1 - probability))

Similarity Weight of the left leaf node 
------------------------------------
 
Similarity Weight = -0.5 + -0.5 ^ 2/ [0.5 * (1 - 0.5) + 0.5 * (1 - 0.5)]
Similarity Weight = 1 / 0.25 + 0.25 
                  = 1 / 0.5 = 2

Similarity Weight of the right leaf node
------------------------------------
Similarity Weight = 0.5 + 0.5 + 0.5 + 0.5 - 0.5 ^ 2/ [0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5)]
Similarity Weight = 2.25 / 1.25 = 1.8

Similarity Weight of the root node
------------------------------------
Similarity Weight = 0.142


Step 3
=========

Total Gain with respect to the split  = 2 + 1.8 - 0.142 = 3.658

????????现在您可以看到，如果我们从 Credit 功能中分离出来，我们可以获得最高的 Gain。然后您可以使用信用功能。您可以对所有组合执行此操作，并选择提供最高增益的根节点特征。

????????好的，现在我选择我的第一个单据作为信用功能，并继续对该功能进行拆分。我必须再次进行二元拆分，我将为第二次拆分选择“薪资”功能，并将其分类为 ≤50K 和 >50K。现在您可以看到有多少数据点超过 ≤50K 和 >50K。

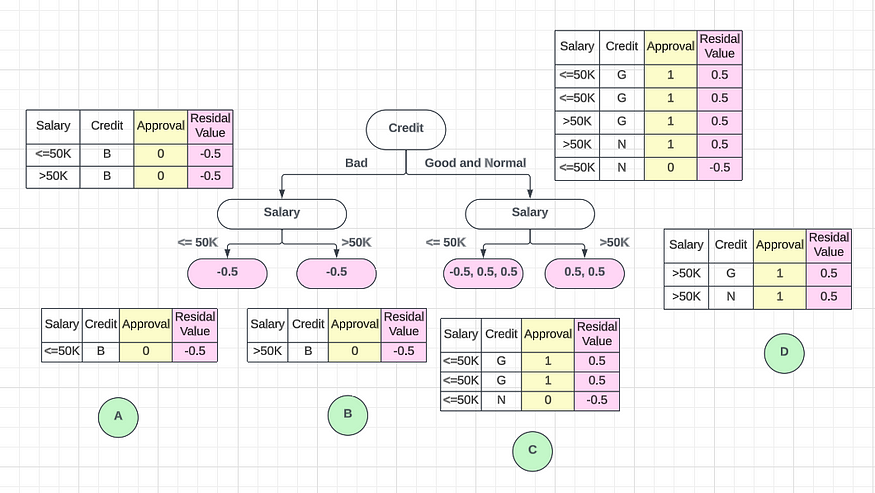
????????现在我们可以计算第二级叶节点的相似度权重。

Leaf Node A:

Similarity Weight = Σ(Residuals) ^2 / Σ(probability * (1 - probability))
                  = -0.5^2 / 0.25 = 0.25 / 0.25 = 1

Leaf Node B:

Similarity Weight = Σ(Residuals) ^2 / Σ(probability * (1 - probability))
                  = -0.5^2 / 0.25 = 0.25 / 0.25 = 1


Root Node:

Similarity Weight = -0.5 + -0.5 ^ 2/ [0.5 * (1 - 0.5) + 0.5 * (1 - 0.5)]
Similarity Weight = 1 / 0.25 + 0.25 
                  = 1 / 0.5 = 2


Leaf Node C:

Similarity Weight = Σ(Residuals) ^2 / Σ(probability * (1 - probability))
                  = (0.5 + 0.5 + -0.5)^2 / (0.25 + 0.25 + 0.25) = 0.25 / 0.25 = 1
                  = 0.25 / 0.75 = 1/3 = 0.33


Leaf Node D:

Similarity Weight = Σ(Residuals) ^2 / Σ(probability * (1 - probability))
                  = (0.5 + 0.5)^2 / (0.25 + 0.25) = 1 / 0.5 = 2

Root Node: 
Similarity Weight = Σ(Residuals) ^2 / Σ(probability * (1 - probability))
                  = 0.5 + 0.5 + 0.5 + 0.5 - 0.5 ^ 2/ [0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5) + 0.5 * (1 - 0.5)]
                  = 2.25 / 1.25 = 1.8



Now we can calculate the Information Gain:
Information Gain  Left Tree = Similarity Weight of A + Similarity Weight of B - Similarity Weight of Root Node 

                            = 1 + 1 - 2 = 0

Information Gain  Left Tree = Similarity Weight of C + Similarity Weight of D - Similarity Weight of Root Node 

                            = 0.33 + 2 - 1.8 = 0.53

????????我们将根据信息增益来比较哪种分割是最好的。现在我已经创建了整个决策树。让我们考虑推理部分。假设一条新记录将进入模型以及我们如何计算输出。首先，该行将转到基本模型。那么基本模型将给出 0.5 的概率。现在我们如何从基本模型计算真实概率？为此，我们可以应用称为Logs的东西。我们可以使用一个公式来计算概率。

P = Base Model Probability
Log (P/1-P)
Log (0.5 / 1 - 0.5) = Log(1) = 0

????????如果我们仔细看看，这等于零。这意味着初始值将为零并通过二元决策树。

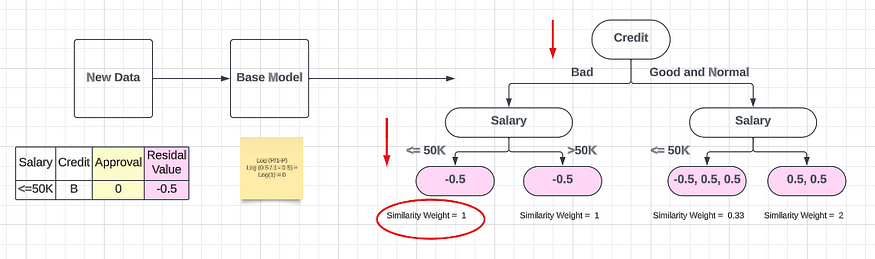
????????所得值将添加到属于不良信用限额且薪资≤ 50K 的分支机构。相似度权重为1，我们传递学习率参数(α)。

0 + α (1)   α = Learning Rate =  0.001

????????将学习率参数乘以相似度权重1，得到参考值。我们使用 Alpha 值（α）作为我们的学习率，它可以是基于我们在其他地方定义的学习参数的最小值。为了解决这个分类问题，我们应用称为 Sigmoid(σ) 的激活函数。这可确保输出值落在零和一之间。

σ (0 + α (1))

????????同样，您也可以创建其他决策树。

????????所以最后你的新记录的输出将是这样的，

σ (0 + α1 (Dicision Tree Similarty Weight1) + α2 (Dicision Tree Similarty Weight2) + α3 (Dicision Tree Similarty Weight3) + α4 (Dicision Tree Similarty Weight4) + ..... + αn (Dicision Tree Similarty Weightn))

????????类似地，该算法会生成多个决策树，并将它们相加组合以生成更好的估计。

四、XGBoost的优点

1. 性能：XGBoost 在各种机器学习任务中产生高质量结果方面拥有良好的记录，尤其是在 Kaggle 竞赛中，它一直是获胜解决方案的热门选择。
2. 可扩展性：XGBoost 专为机器学习模型的高效且可扩展的训练而设计，使其适用于大型数据集。
3. 可定制性：XGBoost 具有广泛的超参数，可以调整这些超参数来优化性能，从而使其高度可定制。
4. 处理缺失值：XGBoost 具有处理缺失值的内置支持，可以轻松处理经常包含缺失值的现实数据。
5. 可解释性：与某些难以解释的机器学习算法不同，XGBoost 提供了特征重要性，可以更好地理解哪些变量在做出预测时最重要。

五、XGBoost 的缺点

1. 计算复杂性：XGBoost 可能是计算密集型的，特别是在训练大型模型时，使其不太适合资源受限的系统。
2. 过度拟合：XGBoost 很容易过度拟合，特别是在小数据集上训练或模型中使用太多树时。
3. 超参数调整：XGBoost 有许多可以调整的超参数，因此正确调整参数以优化性能非常重要。然而，找到最佳参数集可能非常耗时并且需要专业知识。
4. 内存要求：XGBoost 可能会占用大量内存，尤其是在处理大型数据集时，因此不太适合内存资源有限的系统。

这就是 XgBoost 分类器的全部内容。我希望你能更好地理解这个算法。在另一个教程中见。