数值分析总复习
第一章科学计算
误差
解题步骤:
- 先求绝对误差:
∣ x ? x ? ∣ |x - x^*| ∣x?x?∣ - 求相对误差限:
∣ x ?? ? ?? x ? ∣ x ? \frac{|x\,\,-\,\,x^*|}{x^*} x?∣x?x?∣? - 求有效数字
∣ x ? x ? ∣ 需要小于它自身的半个单位 |x-x^*|\text{需要小于它自身的半个单位} ∣x?x?∣需要小于它自身的半个单位,然后算小数点后一共有多少数字
举个例子:
相减得出结果为0.0000345则小于0.0005,则有效数字为4
例题1:

第二章 线性代数直接法
高斯消去法
高斯顺序消去法
解题步骤(假设是一个三行三列的矩阵):
- 先用第一行消去2,3行
- 再用第二行消去第三行
例题1:

例题2:

高斯列主元消去法
解题步骤:
- 比较哪一行的绝对值最大,然后交换
- 用第一行消去第2、3行
- 再次比较哪一行绝对值最大,交换
- 重复步骤
例题1:

例题2:


第三章 线性代数方程组的迭代法
范数和条件数
- 1范数(列范数):每一列元素的绝对值之和的最大值
- 无穷范数(行范数):每一行元素的绝对值之和的最大值
- 2范数:
- 向量:向量元素平方的和的平方根
- 矩阵(又称为谱范数):null
- 无穷范数条件数:
c o n d ∞ ( A ) ?? = ?? ∣ ∣ A ∣ ∣ ∞ ∣ ∣ A ? 1 ∣ ∣ ∞ cond_{\infty}\left( A \right) \,\,=\,\,||A||_{\infty}||A^{-1}||_{\infty} cond∞?(A)=∣∣A∣∣∞?∣∣A?1∣∣∞?
例题1:

例题2:

求 A ? 1 A^{-1} A?1的方法
- 初等变换法

第九章 常微分方程初边值问题数值解
龙格-库塔公式
基本概念
一般问题会有
y
′
,
h
,
f
(
x
)
=
y
y', h , f(x) = y
y′,h,f(x)=y等参数
将其转换为
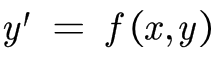
注意h的值,一般是在 0 ≤ x ≤ 1 0 \le x \le 1 0≤x≤1之间,逐渐相加之后递增到1结束计算
四阶四段龙格库塔公式如下:
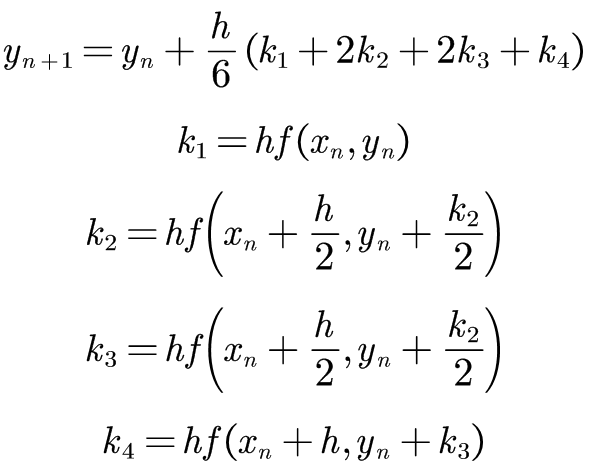
解题步骤
- 将 x 0 , y 0 , h x_0,y_0,h x0?,y0?,h写在旁边
- 将将题目中给出的已知信息代入 k 1 , k 2 , k 3 , k 4 k_1,k_2,k_3,k_4 k1?,k2?,k3?,k4?
- 更新 y n y_n yn?的值
- 重复过程
k 2 k_2 k2?->f的 x n + h 2 x_n+\frac{h}{2} xn?+2h?表示 x x x,同理另外一个表示 y y y,将其代入到f(x,y)中进行化简

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!