MATLAB中cov函数用法

目录

语法

说明

示例

协方差矩阵

两个向量的协方差

两个矩阵的协方差

指定归一化权重

排除缺失值的协方差

---

????????cov函数的功能是计算协方差。

语法

C = cov(A)
C = cov(A,B)
C = cov(___,w)
C = cov(___,nanflag)

说明

C = cov(A) 返回协方差。

• ?如果 A 是由观测值组成的向量，则 C 为标量值方差。

• 如果 A 是其列表示随机变量或行表示观测值的矩阵，则 C 为对应的列方差沿着对角线排列的协方差矩阵。

• 如果 A 是标量，则 cov(A) 返回 0。如果 A 是空数组，则 cov(A) 返回 NaN。

C 按观测值数量 -1 实现归一化。如果仅有一个观测值，应按 1 进行归一化。

C = cov(A,B) 返回两个随机变量 A 和 B 之间的协方差。

• 如果 A 和 B 是长度相同的观测值向量，则 cov(A,B) 为 2×2 协方差矩阵。

• 如果 A 和 B 是观测值矩阵，则 cov(A,B) 将 A 和 B 视为向量，并等价于 cov(A(:),B(:))。A 和 B 的大小必须相同。

• 如果 A 和 B 为标量，则 cov(A,B) 返回零的 2×2 块。如果 A 和 B 为空数组，则 cov(A,B) 返回 NaN 的 2×2 块。

????????C = cov(___,w) 为之前的任何语法指定归一化权重。如果 w = 0（默认值），则 C 按观测值数量 -1 实现归一化。w = 1 时，按观测值数量对它实现归一化。

????????C = cov(___,nanflag) 指定处理输入数组中 NaN 值的条件。例如，cov(A,"omitrows") 在计算协方差时会忽略 A 中包含一个或多个 NaN 值的任何行。默认情况下，cov 包括 NaN 值。

示例

协方差矩阵

????????创建一个 3×4 矩阵并计算它的协方差。

A = [5 0 3 7; 1 -5 7 3; 4 9 8 10];
C = cov(A)
C = 4×4

    4.3333    8.8333   -3.0000    5.6667
    8.8333   50.3333    6.5000   24.1667
   -3.0000    6.5000    7.0000    1.0000
    5.6667   24.1667    1.0000   12.3333

????????由于 A 的列数是 4，结果为 4×4 矩阵。

两个向量的协方差

????????创建两个向量并计算它们的 2×2 协方差矩阵。

A = [3 6 4];
B = [7 12 -9];
cov(A,B)
ans = 2×2

    2.3333    6.8333
    6.8333  120.3333

两个矩阵的协方差

????????创建两个大小相同的矩阵并计算它们的 2×2 协方差。

A = [2 0 -9; 3 4 1];
B = [5 2 6; -4 4 9];
cov(A,B)
ans = 2×2

   22.1667   -6.9333
   -6.9333   19.4667

指定归一化权重

????????创建一个矩阵并计算按行数归一化的协方差。

A = [1 3 -7; 3 9 2; -5 4 6];
C = cov(A,1)
C = 3×3

   11.5556    5.1111  -10.2222
    5.1111    6.8889    5.2222
  -10.2222    5.2222   29.5556

排除缺失值的协方差

????????创建一个包含 NaN 值的矩阵。

A = [1.77 -0.005 3.98; NaN -2.95 NaN; 2.54 0.19 1.01];

????????计算矩阵的协方差，排除包含任一?NaN?值的行。

C = cov(A,"omitrows")
C = 3×3

    0.2964    0.0751   -1.1435
    0.0751    0.0190   -0.2896
   -1.1435   -0.2896    4.4104

参数说明

A — 输入数组

????????输入数组，指定为向量或矩阵。

B — 其他输入数组

????????附加的输入矩阵，指定为向量或矩阵。B 的大小必须与 A 相同。

w — 归一化权重

归一化权重，指定为下列值之一：

• 0 - 输出按观测值数量 -1 实现归一化。如果仅有一个观测值，应按 1 进行归一化。

• 1 - 输出按观测值数量实现归一化。

nanflag — 缺失值条件

缺失值条件，指定为下列值之一：

• "includemissing" 或 "includenan" - 计算协方差时，包含输入数组中的 NaN 值。"includemissing" 和 "includenan" 具有相同的行为。

• "omitrows" - 计算协方差时，忽略输入数组中包含一个或多个 NaN 值的任何行。

• "partialrows" - 对于每个双列协方差计算，仅忽略输入数组中那些成对的包含 NaN 值的行。

C — 协方差

协方差，以标量或矩阵形式返回。

• 对于单矩阵输入，C 基于用 A 表示的随机变量数（列数）提供大小 [size(A,2) size(A,2)]。列的方差沿着对角线排列。如果 A 是行或列向量，则 C 为标量值方差。

• 对于二向量或二矩阵输入，C 是介于两个随机变量之间的 2×2 协方差矩阵。方差沿着 C 的对角线排列。

协方差

????????对于两个随机可变向量 A 和 B，协方差定义为：

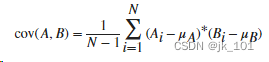
，其中，μA?是 A 的均值，μB?是 B 的均值，*?表示复共轭。

两个随机变量的协方差矩阵是每个变量间成对的协方差计算结果的矩阵，

????????对于矩阵 A，它的列是由观测值组成的随机变量，其协方差矩阵就是每个列组合之间的成对协方差计算结果。换言之，C(i,j)=cov(A(:,i),A(:,j))。

方差

????????对于由 N 个标量观测值组成的有限长向量 A，方差被定义为

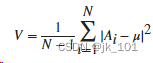
，其中，μ 是 A 的均值，

????????某些方差定义使用 N（而不是 N-1）的归一化因子，可以通过将 w 设置为 1 来指定该因子。在任一情况下，都假定均值包含常见的归一化因子 N。