【BBuf的CUDA笔记】十,Linear Attention的cuda kernel实现解析
欢迎来 https://github.com/BBuf/how-to-optim-algorithm-in-cuda 踩一踩。
0x0. 问题引入
Linear Attention的论文如下: Transformers are RNNs:
Fast Autoregressive Transformers with Linear Attention:https://arxiv.org/pdf/2006.16236.pdf 。官方给出实现代码地址:https://github.com/idiap/fast-transformers 。虽然这个仓库是Linear Attention的原始实现,但基于这个codebase也引出了后续的一系列线性Attention的工作比如:Efficient Attention: Attention with Linear Complexities(https://arxiv.org/abs/1812.01243),Linformer: Self-Attention with Linear Complexity(https://arxiv.org/abs/2006.04768),Reformer: The Efficient Transformer(https://arxiv.org/abs/2001.04451)等等。
这篇文章是对Linear Attention的forward cuda kernel进行解析,在此之前我先基于论文的3.2节对Linear Attention做一个复述,明确这里要计算的是什么。
Linear Attention的目的是将 Self Attention 的平方根序列长度级别复杂度降低为线性的复杂度。假设Attention模块的输入为 x x x,它的shape为 [ N , F ] [N, F] [N,F],其中 N N N表示序列长度, F F F表示的是embedding的维度。对于常见的SelfAttention来说,它的计算过程表示为:

其中矩阵Q、K、V是由输入 x x x经线性变化得到的。如果用下标 i i i来表示矩阵的第 i i i行,那么可以将公式(2)中的计算用如下形式抽象出来:
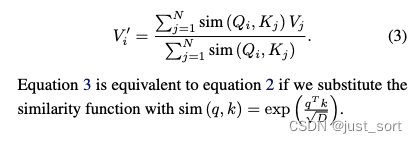
其中sim() 为抽象出的计算Query和Key相似度的函数。在常规的Transformer中,sim()定义为上面的 e x p ( q T k D ) exp(\frac{q^Tk}{\sqrt D}) exp(D?qTk?)。
接着,我们可以将sim()定义为任何我们希望的形式。上述定义过程中对sim()唯一的约束是它需要非负。Linear Transformer采用了kernel来定义上面公式(3)中的sim,这就引出了公式4:
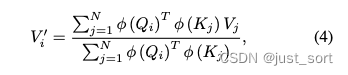
然后在Linear Attention里面
?
\phi
?被定义为
?
(
x
)
=
e
l
u
(
x
)
+
1
\phi(x)=elu(x)+1
?(x)=elu(x)+1 。注意上式中求和项与
i
i
i无关,因此可以把与
i
i
i有关的项提到前面,可以推出公式(5):
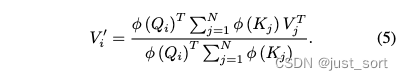
可以想到我们在遍历Q的时候,由于求和项和
i
i
i无关,所以可以提前把右边的求和项计算出来,所以整体的复杂度和序列长度是线性关系而非平方。对应了论文的这部分解释:

上面介绍的是Encoder部分的Linear Attention工作原理,而本篇文章解析的就是使用cuda如何计算和优化上面的公式(5)。
0x1. 接口介绍
我们先从这个naive的Linear Attention实现入手,摸清代码实现和上面介绍的公式5的对应关系。 https://github.com/idiap/fast-transformers/blob/master/fast_transformers/attention/linear_attention.py ,这个实现很短,逐行解释一下。
from ..attention_registry import AttentionRegistry, Optional, Callable, Int, \
EventDispatcherInstance
from ..events import EventDispatcher
from ..feature_maps import elu_feature_map # 这就是论文提到的elu(x)+1
class LinearAttention(Module):
"""实现了未经掩码处理的注意力机制,使用特征映射的点积,在 O(N D^2) 的复杂度下进行计算。
给定query、key和value分别为 Q、K、V,我们不是计算
V' = softmax(Q.mm(K.t()), dim=-1).mm(V),
而是利用一个特征映射函数 Φ(.),执行以下计算
V' = normalize(Φ(Q).mm(Φ(K).t())).mm(V).
上述计算可以在 O(N D^2) 的复杂度下完成,其中 D 是 Q、K 和 V 的维度,N 是序列长度。
然而,根据特征映射的不同,注意力的复杂度可能会受到限制。
Arguments
---------
feature_map: callable, 一个可调用的函数,用于对张量最后一个维度应用特征映射(默认为 elu(x)+1)
eps: float, 一个小数,用于确保分母的数值稳定性(默认为 1e-6)
event_dispatcher: str 或 EventDispatcher 实例,用于此模块进行事件派发的实例(默认为默认的全局调度器)
"""
def __init__(self, query_dimensions, feature_map=None, eps=1e-6,
event_dispatcher=""):
super(LinearAttention, self).__init__()
self.feature_map = (
feature_map(query_dimensions) if feature_map else
elu_feature_map(query_dimensions)
)
self.eps = eps
self.event_dispatcher = EventDispatcher.get(event_dispatcher)
def forward(self, queries, keys, values, attn_mask, query_lengths,
key_lengths):
# 对查询(Q)和键(K)应用特征映射。
self.feature_map.new_feature_map(queries.device)
Q = self.feature_map.forward_queries(queries)
K = self.feature_map.forward_keys(keys)
# 检查并确保 attn_mask 是全部为一的,这表明这种注意力不支持任意的注意力掩码。
if not attn_mask.all_ones:
raise RuntimeError(("LinearAttention does not support arbitrary "
"attention masks"))
K = K * key_lengths.float_matrix[:, :, None, None]
# 计算键和值的点积(KV 矩阵),以此减少计算复杂度。
KV = torch.einsum("nshd,nshm->nhmd", K, values)
# 计算归一化因子(Z)。
Z = 1/(torch.einsum("nlhd,nhd->nlh", Q, K.sum(dim=1))+self.eps)
# 最后,使用 torch.einsum 计算并返回新的值(V)
V = torch.einsum("nlhd,nhmd,nlh->nlhm", Q, KV, Z)
return V.contiguous()
注意,K = K * key_lengths.float_matrix[:, :, None, None] 这行代码是用于在注意力机制的计算中“掩蔽”掉那些序列中的无效或填充部分,确保模型只关注有效的数据部分。这里的key_length表示的是序列中每个元素是否有效,比如在处理具有不同长度的序列时(如在自然语言处理中),较短的序列可能会被 padding 以匹配最长序列的长度。key_lengths 就是用来标识这些 padding 位置的。.float_matrix是将key_lengths转换为浮点数矩阵的操作。[:, :, None, None]这是一个切片操作,用于添加两个额外的维度,用于确保两个张量在进行elementwise乘法之前具有相同的shape。此外,forward的过程中存在爱因斯坦求和表达式,前面2个比较好理解,V = torch.einsum("nlhd,nhmd,nlh->nlhm", Q, KV, Z)这行代码的"nlhd,nhmd,nlh->nlhm"表示的过程为:
- Q 的 d 维度和 KV 的 d 维度会相乘。
- d 维度就会被求和,因为它没有出现在 “nlhm” 中。
- 结果会被重新组织成输出格式 “nlhm” 指定的形状。
这里的代码也就对应着 V’ = normalize(Φ(Q).mm(Φ(K).t())).mm(V) 这个公式。
综上,这里实现的是没有mask的Linear Attention,但目前在主流的解码器架构上进行训练需要的是带因果关系mask的Attention,所以自然也需要一个CausalLinearAttention的实现,而本文要解析的cuda kernel也正是在这个模块引入的。源码见:https://github.com/idiap/fast-transformers/blob/master/fast_transformers/attention/causal_linear_attention.py 。
# 这个函数实现了因果线性注意力的核心计算。它首先调整输入张量 Q、K 和 V的维度,
# 然后应用 causal_dot_product 函数计算新的值张量 V_new。
def causal_linear(Q, K, V):
Q = Q.permute(0,2,1,3).contiguous()
K = K.permute(0,2,1,3).contiguous()
V = V.permute(0,2,1,3).contiguous()
V_new = causal_dot_product(Q, K, V)
return V_new.permute(0,2,1,3).contiguous()
class CausalLinearAttention(Module):
"""实现因果掩码注意力机制,使用特征映射的点积在 O(N D^2) 复杂度下进行计算。
有关用特征映射替换 softmax 的一般概念,请参阅 fast_transformers.attention.linear_attention.LinearAttention。除此之外,我们还利用了因果掩码是三角形掩码的事实,这允许我们在保持 O(N D^2) 复杂度的同时应用掩码并计算注意力。
Arguments
---------
feature_map: callable, 一个可调用的函数,用于对张量最后一个维度应用特征映射(默认为 elu(x)+1)
eps: float, 一个小数,用于确保分母的数值稳定性(默认为 1e-6)
event_dispatcher: str 或 EventDispatcher 实例,用于此模块进行事件派发的实例(默认为默认的全局调度器)
"""
def __init__(self, query_dimensions, feature_map=None, eps=1e-6,
event_dispatcher=""):
super(CausalLinearAttention, self).__init__()
self.feature_map = (
feature_map(query_dimensions) if feature_map else
elu_feature_map(query_dimensions)
)
self.eps = eps
self.event_dispatcher = EventDispatcher.get(event_dispatcher)
# 这个私有方法用于确保 Q 和 K 张量的大小兼容,通过对 K 进行切片或填充以匹配 Q 的大小。
def _make_sizes_compatible(self, Q, K):
"""Either slice or pad K in case that the sizes do not match between Q
and K."""
N, L, H, E = Q.shape
_, S, _, _ = K.shape
if L == S:
return Q, K
if L < S:
return Q, K[:, :L, :, :]
if L > S:
return Q, torch.cat([K, K.new_zeros(N, L-S, H, E)], dim=1)
def forward(self, queries, keys, values, attn_mask, query_lengths,
key_lengths):
# 对query和key应用特征映射。
self.feature_map.new_feature_map(queries.device)
Q = self.feature_map.forward_queries(queries)
K = self.feature_map.forward_keys(keys)
# 检查 attn_mask 是否为下三角因果掩码,并应用键长度掩码。
if not attn_mask.lower_triangular:
raise RuntimeError(("CausalLinearAttention only supports full "
"lower triangular masks"))
K = K * key_lengths.float_matrix[:, :, None, None]
# 确保query和key的大小(长度)兼容。
Q, K = self._make_sizes_compatible(Q, K)
# TODO: Shall we divide the Q and K with a relatively large number to
# avoid numerical instabilities in computing the denominator?
# We used to divide each with the max norm of all q and k but
# that seems relatively costly for a simple normalization.
# Compute the normalizers
Z = 1/(torch.einsum("nlhi,nlhi->nlh", Q, K.cumsum(1)) + self.eps)
# Compute the unnormalized result
V = causal_linear(
Q,
K,
values
)
return V * Z[:, :, :, None]
和full mask的Linear Attention的主要区别就是现在的mask是下三角的,以及 causal_dot_product 这个函数的应用。我们可以从LinearAttention的forward过程推出 causal_dot_product 完成的其实是下面的计算过程:V’ = Φ(Q).mm(Φ(K).t()).mm(V)
0x2. CPU实现
先看一下causal_dot_product的cpu实现,确定它的计算逻辑和上面的结论一致。 https://github.com/idiap/fast-transformers/blob/master/fast_transformers/causal_product/causal_product_cpu.cpp#L10-L125 。下面是一些关键的解释。
// 这个函数计算两个向量 a 和 b 的外积(a 和 b 的转置的点积)并将结果保存在 out 中。
// a 是一个长度为 A 的向量,b 是一个长度为 B 的向量。
// 外积的结果是一个 AxB 的矩阵。
inline void vvt_dot(float *a, float *b, float *out, int A, int B) {
for (int i=0; i<A; i++) {
float * bi = b;
for (int j=0; j<B; j++) {
*out += (*a) * (*bi);
out++;
bi++;
}
a++;
}
}
// 这个函数实现了向量 v 和矩阵 m 的乘积,并将结果保存在 out 中。
// v 是一个长度为 A 的向量,m 是一个 AxB 的矩阵。
// 结果是一个长度为 B 的向量。
inline void vm_dot(float *v, float *m, float *out, int A, int B) {
// TODO: Consider removing the zeroing part and assuming out already
// contains 0s
for (int i=0; i<B; i++) {
out[i] = 0;
}
for (int i=0; i<A; i++) {
float *oi = out;
for (int j=0; j<B; j++) {
*oi += (*v) * (*m);
oi++;
m++;
}
v++;
}
}
// 这个函数计算向量 v 和矩阵 m 转置的乘积,并将结果保存在 out 中。
// v 是一个长度为 B 的向量,m 是一个 AxB 的矩阵。
// 结果是一个长度为 A 的向量。
inline void vmt_dot(float *v, float *m, float *out, int A, int B) {
for (int i=0; i<A; i++) {
float *vi = v;
float s = 0;
for (int j=0; j<B; j++) {
s += (*vi) * (*m);
vi++;
m++;
}
// TODO: Should we be aggregating? See the comment on vm_dot.
*out = s;
out++;
}
}
// 这个函数计算查询(queries)、键(keys)和值(values)的因果掩码点积。
// N、H、L 和 E 分别代表 batch 大小、头数、序列长度和特征维度。M 是value的特征维度。
// 计算公式为:V_j' = (Q_{0:j} * K_{0:j}^T) * V_{0:j}
void causal_dot_product(
const torch::Tensor queries,
const torch::Tensor keys,
const torch::Tensor values,
torch::Tensor product
) {
// Extract some shapes
int N = queries.size(0);
int H = queries.size(1);
int L = queries.size(2);
int E = queries.size(3);
int M = values.size(3);
// Create accessors for all the arguments
auto qa = queries.accessor<float, 4>();
auto ka = keys.accessor<float, 4>();
auto va = values.accessor<float, 4>();
auto pa = product.accessor<float, 4>();
// 使用 OpenMP 实现并行计算,增加计算效率。
#pragma omp parallel for collapse(2)
for (int n=0; n<N; n++) {
for (int h=0; h<H; h++) {
auto kv = torch::zeros({E, M}, queries.options());
float *kvp = kv.data_ptr<float>();
for (int l=0; l<L; l++) {
// 该函数首先计算 K 和 V 的外积(vvt_dot),然后计算 Q 和这个外积的结果(vm_dot)。
vvt_dot(
&ka[n][h][l][0],
&va[n][h][l][0],
kvp,
E,
M
);
vm_dot(
&qa[n][h][l][0],
kvp,
&pa[n][h][l][0],
E,
M
);
}
}
}
}
可以清晰的看到这里的计算过程就是 V j ′ = ( Q 0 : j ? K 0 : j T ) ? V 0 : j V_j' = (Q_{0:j} * K_{0:j}^T) * V_{0:j} Vj′?=(Q0:j??K0:jT?)?V0:j? ,也就是先计算 K 和 V 的外积(vvt_dot),然后计算 Q 和这个外积的结果(vm_dot)。为了更高效,还使用了openmp做并行计算。
0x3. CUDA实现
cuda实现在 https://github.com/idiap/fast-transformers/blob/master/fast_transformers/causal_product/causal_product_cuda.cu 。
Fallback 的 causal_dot_product_kernel
由于整个kernel的行数有点多,这里先只关注forward的kernel,我去掉了大部分的backward的kernel,精简后的代码放在这里:https://github.com/BBuf/how-to-optim-algorithm-in-cuda/blob/master/linear-attention/causal_product_cuda.cu 。
首先来到kernel的入口:
void causal_dot_product(const torch::Tensor queries,
const torch::Tensor keys,
const torch::Tensor values,
torch::Tensor product) {
#ifdef ENABLE_NVIDIA_OPTIMIZATIONS
int fallback = nvidia::lmha_fwd(queries, keys, values, product);
#else
int fallback = 1;
#endif
if( fallback ) {
causal_dot_product_(queries, keys, values, product);
}
}
PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
m.def(
"causal_dot_product",
&causal_dot_product,
"Compute the weighted sum of values but attending only to previous "
"values."
);
}
这里值得注意的地方就是如果开启了ENABLE_NVIDIA_OPTIMIZATIONS才会走优化实现,否则会fallback到causal_dot_product_这个kernel,我们看一下causal_dot_product_ kernel的实现。
typedef torch::PackedTensorAccessor32<float, 4, torch::RestrictPtrTraits> float_accessor;
#define E_BLOCK_SIZE 8
__global__ void causal_dot_product_kernel(
const float_accessor queries,
const float_accessor keys,
const float_accessor values,
float_accessor result,
const int N,
const int H,
const int L,
const int E,
const int M
) {
int n = blockIdx.y; // 确定 batch 所在的id
int h = blockIdx.z; // 确定 attention 所在的头的id
int e_start = blockIdx.x * E_BLOCK_SIZE; // 确定query的特征维度的开始位置
int m = threadIdx.x % M; // 确定 value 的特征维度 id
extern __shared__ float shared_mem[]; // 使用共享内存 (shared_mem) 来临时存储 key 和 value 的乘积。
float* shared_kv = shared_mem;
// 共享内存的初始化
for (int e_local = 0; e_local < E_BLOCK_SIZE && e_local + e_start < E; e_local++) {
shared_kv[m + e_local * M] = 0;
}
for (int t=0; t<L; t++) {
// 对于每个 query 元素,计算与 key 的点积,结果累加到 result 张量中。
float res = 0;
for (int e_local = 0; e_local < E_BLOCK_SIZE && e_local + e_start < E; e_local++) {
shared_kv[e_local*M + m] += keys[n][h][t][e_local + e_start] * values[n][h][t][m];
res += queries[n][h][t][e_local + e_start] * shared_kv[e_local*M + m];
}
atomicAdd(
&result[n][h][t][m],
res
);
}
}
// queries, keys, values 这些都是shape为 [N, H, L, E] 的四维Tensor,通过 float_accessor 访问数据。
void causal_dot_product_(const torch::Tensor queries,
const torch::Tensor keys,
const torch::Tensor values,
torch::Tensor product) {
// 确保使用正确的gpu设置。
torch::DeviceGuard _guard(queries.device());
// N、H、L 和 E 分别代表 batch 大小、头数、序列长度和特征维度。M 是value的特征维度。
int N = queries.size(0);
int H = queries.size(1);
int L = queries.size(2);
int E = queries.size(3);
int M = values.size(3);
// 每个Block处理E_BLOCK_SIZE(=8)个隐藏层的元素
// 一共需要blocks_per_sequence这么多个Block来进行处理
// 注意:这里的blocks_per_sequence还要乘以N和H才是真正的Block个数
const int blocks_per_sequence = (E + E_BLOCK_SIZE - 1) / E_BLOCK_SIZE;
// 每个Block固定有M个线程
dim3 blockDim(M, 1, 1);
dim3 gridDim(blocks_per_sequence, N, H);
// 每个Block固定使用 E_BLOCK_SIZE(=8)* M个float这么大的shm
const int shared_mem_forward = E_BLOCK_SIZE * M * sizeof(float);
causal_dot_product_kernel<<<gridDim, blockDim, shared_mem_forward>>>(
queries.packed_accessor32<float, 4, torch::RestrictPtrTraits>(),
keys.packed_accessor32<float, 4, torch::RestrictPtrTraits>(),
values.packed_accessor32<float, 4, torch::RestrictPtrTraits>(),
product.packed_accessor32<float, 4, torch::RestrictPtrTraits>(),
N, H, L, E, M
);
}
总的来说,这个kernel使用了(E + E_BLOCK_SIZE - 1) / E_BLOCK_SIZE * N * H个Block,并且每个Block里面有M个线程,并且每个Block里面开了一个长度为E_BLOCK_SIZE * M的共享内存来存储当前Block计算出来的KV乘积。
可以这么来想,如果共享内存足够大,那么我们完全可以每个Block处理完一行Q和一行V的计算,也就是E和M做外积得到E*M的矩阵,但是实际上每个Block可以使用的共享内存是有限的,所以在保证线程数为M的情况下,我们每次只能处理一部分的Q,这里就是E_BLOCK_SIZE个,然后处理之后我们要使用atomic_add进行累加,这样才可以保证结果的正确性。
当然,使用了原子加,性能自然会下降,这是考虑共享内存大小和线程数的一个折中,此外虽然key和value的中间结果被存储到了共享内存,但对query的访问依然是走的global memory。接下来我们将看到新的kernel是如何一一解决这些问题。
更优的 lmha_fwd kernel(shared memory+double buffering+free atomic add+pack)
接下来就逐步解析一下lmha_fwd kernel。首先是kernel的dispatch逻辑:
// 此函数的目的是初始化和设置 Lmha_params<T> 结构体的参数,这些参数用于后续的线性多头自注意力操作。
template< typename T >
inline void set_params(Lmha_params<T> ¶ms,
const torch::Tensor q,
const torch::Tensor k,
const torch::Tensor v,
torch::Tensor o) {
// Define the pointers.
// 使用 .data_ptr<T>() 方法获取张量的指针,并将其分配给 params 结构体的对应成员。
params.out = o.data_ptr<T>();
params.q = q.data_ptr<T>();
params.k = k.data_ptr<T>();
params.v = v.data_ptr<T>();
// Define the strides.
// 使用 .stride() 方法获取张量各维度的步长,并存储在 params 结构体中。
params.q_stride_B = (int) q.stride(0);
params.q_stride_H = (int) q.stride(1);
params.q_stride_L = (int) q.stride(2);
params.k_stride_B = (int) k.stride(0);
params.k_stride_H = (int) k.stride(1);
params.k_stride_L = (int) k.stride(2);
params.v_stride_B = (int) v.stride(0);
params.v_stride_H = (int) v.stride(1);
params.v_stride_L = (int) v.stride(2);
params.o_stride_B = (int) o.stride(0);
params.o_stride_H = (int) o.stride(1);
params.o_stride_L = (int) o.stride(2);
// 从query张量 q 中提取出维度信息(如批量大小 N、头数 H、序列长度 L 和特征维度 E)并设置到 params 结构体中。
int N = q.size(0);
int H = q.size(1);
int L = q.size(2);
int E = q.size(3);
int M = v.size(3);
params.B = N;
params.L = L;
params.H = H;
params.E = E;
params.M = M;
}
int lmha_fwd(const torch::Tensor queries,
const torch::Tensor keys,
const torch::Tensor values,
torch::Tensor product) {
// Make sure that we are using the correct GPU device
torch::DeviceGuard _guard(queries.device());
// Make sure the inner-most dimension of the tensors is packed.
// 使用 assert 语句检查张量的最内层维度(即特征维度)是否是packed的
assert(queries.stride(3) == 1);
assert(keys .stride(3) == 1);
assert(values .stride(3) == 1);
assert(product.stride(3) == 1);
// 提取张量的维度信息,如批量大小、头数、序列长度等。
int N = queries.size(0);
int H = queries.size(1);
int L = queries.size(2);
int E = queries.size(3);
int M = values.size (3);
// The structure of params.
Lmha_params<float> params;
// 调用 set_params 函数来初始化 Lmha_params<float> 结构体。
set_params(params, queries, keys, values, product);
// 调用 lmha<false>(params) 函数来执行实际的线性多头自注意力计算。这里 lmha<false> 表示特定的模板实例化。
return lmha<false>(params);
}
这段代码主要是做了一些预处理工作也就是设置Lmha_params对象,然后调用lmha<false>这个函数来执行线性多头自注意力计算,这里的fasle意思是这里执行的是forward计算。另外需要注意的是,虽然这里命名是线性多头自注意力,但实际上计算的东西还是上面讲的causal_dot_product。
接下来看一下 lmha 这个模板函数的实现。
// GO_BACKWARD: 一个布尔类型的模板参数,用于指示是进行前向计算还是反向计算。
template< bool GO_BACKWARD >
int lmha(const Lmha_params<float> ¶ms) {
int blocks = params.B * params.H; // blocks表示GPU的block数量?
int res = 1;
if( blocks < LOW_OCCUPANCY_THRESHOLD ) {
if( params.E <= 32 ) {
res = lmha_low_occupancy_< 32, GO_BACKWARD>(params, blocks);
} else if( params.E <= 64 ) {
res = lmha_low_occupancy_< 64, GO_BACKWARD>(params, blocks);
} else if( params.E <= 128 ) {
res = lmha_low_occupancy_<128, GO_BACKWARD>(params, blocks);
} else if( params.E <= 256 ) {
res = lmha_low_occupancy_<256, GO_BACKWARD>(params, blocks);
}
} else {
if( params.E <= 32 ) {
res = lmha_< 32, 1, GO_BACKWARD>(params);
} else if( params.E <= 48 ) {
res = lmha_< 48, 1, GO_BACKWARD>(params);
} else if( params.E <= 64 ) {
res = lmha_< 64, 1, GO_BACKWARD>(params);
} else if( params.E <= 128 ) {
res = lmha_<128, 2, GO_BACKWARD>(params);
} else if( params.E <= 256 ) {
res = lmha_<256, 4, GO_BACKWARD>(params);
}
}
return res;
}
可以看到如果blocks(batch 和 注意力头的乘积 params.B * params.H)小于LOW_OCCUPANCY_THRESHOLD(=40)的时候,走的是lmha_low_occupancy_这个kernel的实现,否则就会走到lmha_的实现。另外,还会根据 query 的特征维度的大小 E 来设置kernel不同的模板参数。先来看一下lmha_这个常规一些的实现:
// 确定lmha kernel需要的共享内存大小
template< int E, typename Params >
static inline __device__ __host__ int smem_buffer_elts_(const Params ¶ms) {
int M = round_up(params.M, 4);
return 2*E + 2*M;
}
// E: 代表特征维度的大小。
// THREADS_PER_HEAD: 每个 attention 头分配的线程数。
// GO_BACKWARD: 布尔类型的模板参数,指示是进行前向计算还是反向传播。
template< int E, int THREADS_PER_HEAD, bool GO_BACKWARD >
int lmha_(const Lmha_params<float> ¶ms) {
// 调整 M 维度: M 是 params.M 的调整值,向上取整到最接近的 4 的倍数。这种调整可能是出于内存对齐或性能优化的考虑。
int M = round_up(params.M, 4);
// 计算 CUDA kernel中每个block的线程数。这个数是 E 和 M*THREADS_PER_HEAD 的最大值向上取整到最接近的 32 的倍数。
int block = round_up(max(E, M*THREADS_PER_HEAD), 32);
// 如果计算出的块大小超过 512,或者批量大小 (params.B) 超过 65535,则返回 1。
// 这种情况表示配置不适合有效执行。
if( block > 512 || params.B > 65535 ) {
return 1;
}
// grid: 定义了 CUDA 核函数的网格大小,它是由头数 (params.H) 和批量大小 (params.B) 组成的二维网格。
dim3 grid(params.H, params.B);
// smem: 计算共享内存的大小,基于函数 smem_buffer_elts_<E> 的返回值,它根据特征维度 E 来确定共享内存的元素数量。
size_t smem = smem_buffer_elts_<E>(params)*2*sizeof(float);
// 使用 CUDA 的 <<<grid, block, smem>>> 语法调用 lmha_kernel 核函数,这个函数实际上执行线性多头自注意力的计算工作。
lmha_kernel<E, THREADS_PER_HEAD, GO_BACKWARD><<<grid, block, smem>>>(params);
return 0;
}
可以看到这个 kernel 将会启动H*B个Block,每个Block里面的线程数由 E 以及 M*THREADS_PER_HEAD 共同决定。注意,E 是 query 的隐藏层大小,而 M 是 value 的隐藏层大小。此外,还通过smem_buffer_elts_函数确定了这个kernel需要的共享内存大小,这个函数里面的2*表示的是double buffering。
接下来就是最关键的 lmha_kernel 的实现了,阅读之前还是要先想着我们要计算的东西是 V j ′ = ( Q 0 : j ? K 0 : j T ) ? V 0 : j V_j' = (Q_{0:j} * K_{0:j}^T) * V_{0:j} Vj′?=(Q0:j??K0:jT?)?V0:j? ,也就是先计算 K 和 V 的外积(vvt_dot),然后计算 Q 和这个外积的结果(vm_dot)。
// 确定lmha kernel需要的共享内存大小
template< int E, typename Params >
static inline __device__ __host__ int smem_buffer_elts_(const Params ¶ms) {
int M = round_up(params.M, 4);
return 2*E + 2*M;
}
// E: 特征维度的大小。
// THREADS_PER_HEAD: 每个 attention 头分配的线程数。
// GO_BACKWARD: 布尔类型的模板参数,指示是进行前向计算还是反向传播。
// params: Lmha_params<float> 类型的结构体,包含多头自注意力所需的各种参数。
template< int E, int THREADS_PER_HEAD, bool GO_BACKWARD >
__global__
void lmha_kernel(Lmha_params<float> params) {
// Make sure E is a multiple of 4.
static_assert(E % 4 == 0, "");
// The amount of shared memory per buffer (2 buffers for double-buffering).
const int smem_buffer_elts = smem_buffer_elts_<E>(params);
// The M dimension for shared memory.
const int M = round_up(params.M, 4);
// Shared memory to store Q, K and V. Size is 2*smem_buffer_elts.
// 分配共享内存用于存储 Q、K、V(query、key、value)。
// 注意上面的smem_buffer_elts是 (2E + 2M)
extern __shared__ float smem_[];
// The various shared memory buffers.
float *smem_q = &smem_[0*E];
float *smem_k = &smem_[1*E];
float *smem_v = &smem_[2*E];
float *smem_o = &smem_[2*E + M];
// The index of the shared memory buffer (for double-buffering).
// 使用 smem_curr 管理双缓冲区策略,以平滑地在不同迭代间交换共享内存。
int smem_curr = 0;
// 确定处理的序列(bi)和头(hi)。
const int bi = blockIdx.y;
const int hi = blockIdx.x;
// 线程的id
const int tidx = threadIdx.x;
// 根据线程索引(tidx)和 params 中的 stride 计算 Q、K、的偏移量
// The offset to the position loaded by the thread in Q.
int offset_q = bi*params.q_stride_B + hi*params.q_stride_H + tidx;
// The offset to the position loaded by the thread in K.
int offset_k = bi*params.k_stride_B + hi*params.k_stride_H + tidx;
// Determine the base pointers for Q and K.
const float *ptr_q = ¶ms.q[offset_q];
const float *ptr_k = ¶ms.k[offset_k];
// 根据线程索引(tidx)和 params 中的 stride 计算 V、O 的偏移量
int offset_v = bi*params.v_stride_B + hi*params.v_stride_H + tidx;
int offset_o = bi*params.o_stride_B + hi*params.o_stride_H + tidx;
// Determine the base pointers for V.
const float *ptr_v = ¶ms.v[offset_v];
// 通过tidx是否在E的范围内判断当前线程是否是处理Q 和 K的线程
const int active_qk = tidx < params.E;
// 对于处理 Q 和 K 的线程,从全局内存加载数据。
float ldg_q = 0.f, ldg_k = 0.f;
if( active_qk ) {
ldg_q = *ptr_q;
ldg_k = *ptr_k;
}
// Is it an active V thread?
// 同样判断当前线程是否是处理V的活跃线程
const int active_v = tidx < params.M;
// 对于处理V的线程,从全局内存加载数据
float ldg_v = 0.f;
if( active_v ) {
ldg_v = *ptr_v;
}
// Move the load pointers.
// 这里的stride_L实际上就是在E和M的维度上进行整体移动
if( GO_BACKWARD ) {
ptr_q -= params.q_stride_L;
ptr_k -= params.k_stride_L;
ptr_v -= params.v_stride_L;
} else {
ptr_q += params.q_stride_L;
ptr_k += params.k_stride_L;
ptr_v += params.v_stride_L;
}
// 每个注意力头的 float4 元素数量
constexpr int FLOAT4s_PER_HEAD = E / 4;
// 每个线程处理的 float4 元素数量。
constexpr int FLOAT4s_PER_THREAD = FLOAT4s_PER_HEAD / THREADS_PER_HEAD;
// 使用 float4 类型数组 kv 来存储 K 和 V 的乘积。FLOAT4s_PER_THREAD 是每个线程处理的 float4 元素数量。
float4 kv[FLOAT4s_PER_THREAD];
#pragma unroll
for( int ii = 0; ii < FLOAT4s_PER_THREAD; ++ii ) {
kv[ii] = make_float4(0.f, 0.f, 0.f, 0.f);
}
// 输出的指针位置
float *out_ptr = ¶ms.out[offset_o];
// 把q和k存储到shared memory
if( tidx < E ) {
smem_q[smem_curr*smem_buffer_elts + tidx] = ldg_q;
smem_k[smem_curr*smem_buffer_elts + tidx] = ldg_k;
}
// 把v也存储到shared memory
if( tidx < M ) {
smem_v[smem_curr*smem_buffer_elts + tidx] = ldg_v;
}
// 计算每个线程在 V 维度上的位置,用于后续操作。
int vo = tidx / THREADS_PER_HEAD;
int vi = tidx % THREADS_PER_HEAD;
// 遍历每一个时间步(params.L),进行线性多头自注意力计算。
//(回想一下,输入Tensor的形状是 N H L E/M)
for( int ti = 0; ti < params.L; ++ti ) {
// 判断当前迭代是否为最后一次迭代。
int is_last = ti == params.L - 1;
// 如果不是最后一次迭代且当前线程用于处理 Q 或 K,那么从全局内存加载 Q 和 K 的下一个值。
if( !is_last && active_qk ) {
ldg_q = *ptr_q;
ldg_k = *ptr_k;
}
// 同样,如果不是最后一次迭代且当前线程用于处理 V,那么从全局内存加载 V 的下一个值。
if( !is_last && active_v ) {
ldg_v = *ptr_v;
}
// 根据 GO_BACKWARD 标志,移动 Q、K 和 V 的指针,以便加载下一组数据。
if( GO_BACKWARD ) {
ptr_q -= params.q_stride_L;
ptr_k -= params.k_stride_L;
ptr_v -= params.v_stride_L;
} else {
ptr_q += params.q_stride_L;
ptr_k += params.k_stride_L;
ptr_v += params.v_stride_L;
}
// 使用 __syncthreads() 来同步线程,确保所有数据都已经加载到共享内存中。
__syncthreads();
// 每个线程从共享内存中加载 K 的值。使用 float4 来提高数据访问的效率。
float4 k[FLOAT4s_PER_THREAD];
#pragma unroll
for( int ii = 0; ii < FLOAT4s_PER_THREAD; ++ii ) {
int ki = tidx % THREADS_PER_HEAD * 4 + ii * THREADS_PER_HEAD * 4;
k[ii] = *reinterpret_cast<const float4*>(&smem_k[smem_curr*smem_buffer_elts + ki]);
}
// 每个线程加载单个 V 的值。
float v = 0.f;
if( vo < params.M ) {
v = *reinterpret_cast<const float *>(&smem_v[smem_curr*smem_buffer_elts + vo]);
}
// 计算 K*V^T
#pragma unroll
for( int ii = 0; ii < FLOAT4s_PER_THREAD; ++ii ) {
kv[ii].x += k[ii].x * v;
kv[ii].y += k[ii].y * v;
kv[ii].z += k[ii].z * v;
kv[ii].w += k[ii].w * v;
}
// 类似地,从共享内存中加载 Q 的值。
float4 q[FLOAT4s_PER_THREAD];
#pragma unroll
for( int ii = 0; ii < FLOAT4s_PER_THREAD; ++ii ) {
int qi = tidx % THREADS_PER_HEAD * 4 + ii * THREADS_PER_HEAD * 4;
q[ii] = *reinterpret_cast<const float4*>(&smem_q[smem_curr*smem_buffer_elts + qi]);
}
// 使用 Q 和 K*V^T 的乘积来计算每个线程的部分输出值。
float sum = 0.f;
#pragma unroll
for( int ii = 0; ii < FLOAT4s_PER_THREAD; ++ii ) {
sum += q[ii].x * kv[ii].x;
sum += q[ii].y * kv[ii].y;
sum += q[ii].z * kv[ii].z;
sum += q[ii].w * kv[ii].w;
}
// 当每个注意力头有多于一个线程时,需要汇总这些线程的计算结果。
if( THREADS_PER_HEAD > 1 ) {
// 使用 __shfl_xor_sync 函数进行汇总。这个函数能够在 warp 内部的所有线程间高效地交换数据。
// 通过这种方式,线程可以获取并累加其他线程的 sum 变量。
// mask 用于指定参与交换的线程。每次迭代,mask 减半,意味着交换的范围越来越小,最终实现全局汇总。
#pragma unroll
for( int mask = THREADS_PER_HEAD / 2; mask >= 1; mask /= 2 ) {
sum += __shfl_xor_sync(uint32_t(-1), sum, mask);
}
// 如果当前线程对应的 V 维度索引 vo 小于 M 且在其头内的索引 vi 为 0,
// 则将汇总后的 sum 存储到共享内存的输出部分。
if( vo < M && vi == 0 ) {
smem_o[smem_curr*smem_buffer_elts + vo] = sum;
}
// 使用 __syncthreads() 来确保所有线程都完成了对共享内存的写操作。
__syncthreads();
// 活跃的处理 V 的线程读取共享内存中的汇总结果到 sum 变量中。
if( active_v ) {
sum = smem_o[smem_curr*smem_buffer_elts + tidx];
}
} // THREADS_PER_HEAD > 1.
// 活跃的处理 V 的线程将汇总结果写入全局内存的输出位置。
if( active_v ) {
*out_ptr = sum;
}
// 根据 GO_BACKWARD 标志移动输出指针,为下一步迭代做准备。
if( GO_BACKWARD ) {
out_ptr -= params.o_stride_L;
} else {
out_ptr += params.o_stride_L;
}
// 切换共享内存缓冲区,以便在下一个时间步中使用。
smem_curr = (smem_curr + 1) % 2;
// 如果不是最后一次迭代,存储下一步迭代的 Q、K 和 V 到共享内存中。
if( !is_last && tidx < E ) {
smem_q[smem_curr*smem_buffer_elts + tidx] = ldg_q;
smem_k[smem_curr*smem_buffer_elts + tidx] = ldg_k;
}
if( !is_last && tidx < M ) {
smem_v[smem_curr*smem_buffer_elts + tidx] = ldg_v;
}
}
}
kernel里面从shared memory加载Q,K,V的时候的索引代码不是很好理解,这里单独解释一下,以加载K为例:
float4 k[FLOAT4s_PER_THREAD];
#pragma unroll
for( int ii = 0; ii < FLOAT4s_PER_THREAD; ++ii ) {
int ki = tidx % THREADS_PER_HEAD * 4 + ii * THREADS_PER_HEAD * 4;
k[ii] = *reinterpret_cast<const float4*>(&smem_k[smem_curr*smem_buffer_elts + ki]);
}
这里的目的是给每个线程加载一组 float4 类型的 Key 值到局部数组 k 中,FLOAT4s_PER_THREAD 表示每个线程要处理的float4的元素数量,THREADS_PER_HEAD 表示每个注意力头需要分配的线程数,以及tidx表示的是当前的线程索引。
tidx % THREADS_PER_HEAD 这行代码标识当前线程在它所属的注意力头中的局部索引。由于每个注意力头有 THREADS_PER_HEAD 个线程,取模操作确保了索引在 0 到 THREADS_PER_HEAD - 1 的范围内。然后*4用于确保我们访问的是连续的 float4 元素。
接着,ii 是循环变量,从 0 到 FLOAT4s_PER_THREAD - 1。这一步是为了在整个 Key 共享内存中跳过前面所有线程已经处理的部分。乘以 THREADS_PER_HEAD * 4 是因为每个线程负责 FLOAT4s_PER_THREAD 个 float4 元素。
再之后,索引 ki 是以上两部分的和,它确定了当前线程应该从共享内存 smem_k 中读取 K 值的起始位置。
最后,当计算出正确的索引 ki后,kernel就通过 *reinterpret_cast<const float4*>(&smem_k[smem_curr*smem_buffer_elts + ki]) 从共享内存中加载 float4 类型的 Key 值。这里使用了 reinterpret_cast 来确保将共享内存中的数据正确地解释为 float4 类型。
最后,对这个kernel的计算逻辑以及线程配置做一个总结:
- block size:每个块的线程数计算基于
E和M*THREADS_PER_HEAD的最大值,向上取整到最近的 32 的倍数。 - grid size:由头数(H)和批量大小(B)组成的二维网格。
- 共享内存大小:由 smem_buffer_elts_ 函数计算,考虑到特征维度和双缓冲策略。
计算逻辑为:
- 加载和存储 Q、K、V:
- 根据线程索引和参数中的 stride(步长),计算 Q、K 和 V 的偏移量。
- 将 Q、K 和 V 的值加载到共享内存中。
- 计算 K*V^T 乘积:
- 每个线程从共享内存中加载 K 和单个 V 值。
- 计算 K 和 V 的乘积,并累加到局部内存中。
- 加载 Q 值并计算输出:
- 从共享内存中加载 Q 值。
- 使用 Q 和 K*V^T 的乘积来计算每个线程的部分输出值。
- 汇总计算结果:
- 当每个注意力头有多个线程时,使用
__shfl_xor_sync函数在 warp 内部进行数据交换,实现线程间的汇总。
- 当每个注意力头有多个线程时,使用
- 存储输出:
- 将汇总后的结果存储到输出指针指向的全局内存位置。
- 更新指针和缓冲区:
- 根据 GO_BACKWARD 标志更新指针位置。
- 切换共享内存缓冲区以备下一次迭代使用。
这个kernel的执行条件是 B * H 比较大(>40),也就是说可以保证 Block 的数量比较多,这个时候可以获得更高的GPU利用率。但如果 B * H 比较小的时候,如果还是调用这个 kernel,那就会导致 Block 的数量较少,比较难打满 GPU ,所以对于这种情况上面还提供了另外一个 kernel,即:lmha_low_occupancy_kernel 用于在 B * H 比较小时尽可能提高occupancy。但是这个kernel我目前还没完全看明白,等看明白了有机会再分析。
0x4. 总结
本文主要是对Linear Transformer的核心组件Linear Attention进行了原理讲解,并对实现Linear Attention组件的forward cuda kernel进行了详细解析,但这里的实现涉及到3个cuda kernel,分别在不同的数据规模和优化选项下触发,这里只解析了其中的两个。对于 lmha_low_occupancy_kernel 等看明白了有机会再分享。
0x5. 参考
- https://www.zhihu.com/question/602564718
- https://arxiv.org/pdf/2006.16236.pdf
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!