【期末复习向】走进MLP多层感知机

mlp多层感知机，属于最简单的人工神经网络，也被称为全连接神经网络、前馈网络。它是了解神经网络的基础，包括输入层、隐藏层和输出层3个架构。输入层就是具有维度的向量，输出层也是向量。只有隐藏层是包括了所谓的人造神经元。

输入层

输入层即1个向量，向量的维度是由事物本身的特征决定的，根据任务需要确定。

隐藏层

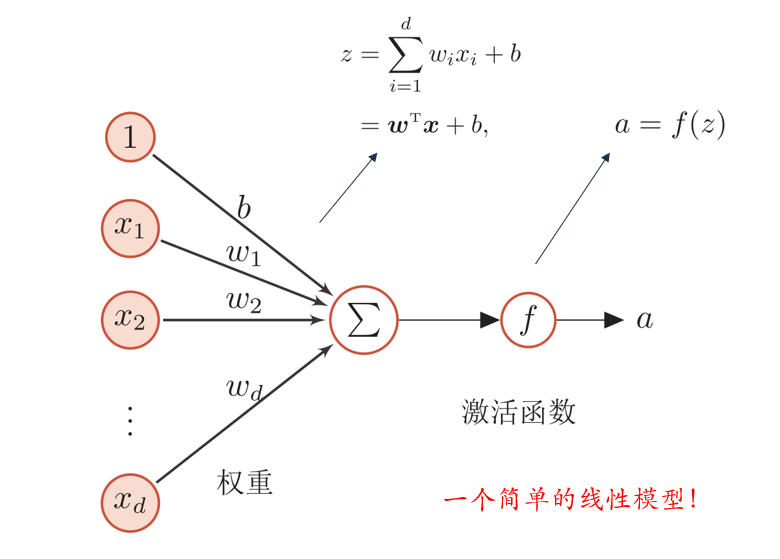
隐藏层是由多个神经元组成的，同时我们常说的神经网络的层数，就是指的隐藏层的个数，有时会算上输入层。其中每个隐藏层由它的权重矩阵和使用的激活函数构成，最简单的隐藏层是，f(w1x1 + b1)，其中w是权重矩阵，b1是偏置，而外面套的f则属于激活函数。

（1）激活函数

激活函数包括sigmoid，tanh，logistics等，具体介绍参考这篇文章：

【期末复习向】常见的激活函数-CSDN博客文章浏览阅读120次，点赞2次，收藏3次。激活函数是非线性的函数，使用它的原因就是因为线性函数无论叠加多少层，最终带来的变化都是线性的组合，一般也只能用于线性分类，如经典的多层感知机。但是如果加上非线性的变换，根据通用近似定理，就可使得神经网络无限逼近任意函数，可以解决的问题范围也就大大增加了。下面举例3个常见的激活函数，sigmoid、tanh、relu及其变种。sigmoid也叫logistics函数它的输出恒大于0如图所示，值域是在0-1的。relu属于非饱和函数，即不存在训练饱和的问题，但是容易导致梯度爆炸问题。而Tanh函数是零中心化。https://blog.csdn.net/weixin_62588253/article/details/134985006?spm=1001.2014.3001.5501（2）权重矩阵

权重矩阵的值在MLP全连接神经网络中是每个神经元和输入向量或者其他神经元连线的权重。它最初的值是通过随机设置的，后续通过反向传播即bp算法进行参数的更新。

（3）参数更新?

具体来说，进行参数的更新需要涉及到数据集，反向传播算法，损失函数，梯度下降，学习率，链式法则。每个数据集包括了x特征向量和y真实值。然后让x向量经过完整的神经网络（前向/正向传播）计算出模型的预测值；随后根据反向传播算法，从后往前依次计算每个权重对损失函数的梯度，并根据梯度下降算法更新权重（用原来的权重-学习率*权重对损失函数的导数）。而想要计算前面的权重对损失函数的导数就需要用到链式法则

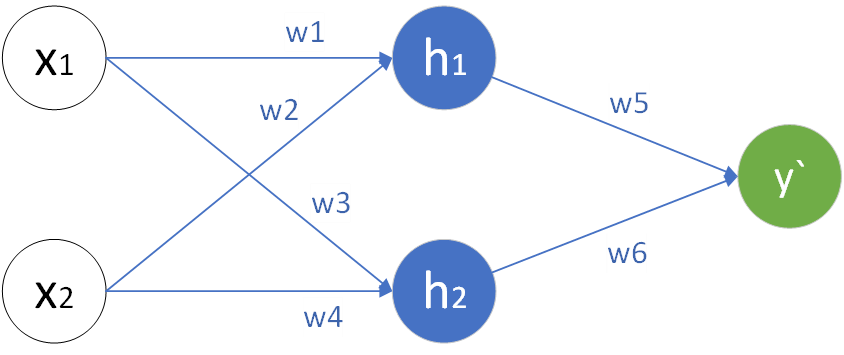
如图，y`是预测值，它可以直接计算w5,w6对损失函数的梯度；但是要计算w1-w4的梯度，则要借助链式法则。在计算完所有权重的梯度后就可以结合学习率更新参数，那么这样就完成了一轮参数的更新。

（4）数据集划分

当然数据集的使用也有讲究，根据每次训练使用的数据集数量不同，采用的梯度下降算法也有所不同。一种是全部的样本用来求loss,这种方式称为批量梯度下降(BGD)；一种是随机的选取一个样本，求loss，进而求梯度，这种方式称为随机梯度下降(SGD)；BGD和SGB的这种，产生了第三种梯度下降的方法：小批量梯度下降(MBGD)。更多细节可以参考下面这篇文章：

https://www.cnblogs.com/lliuye/p/9451903.htmlhttps://www.cnblogs.com/lliuye/p/9451903.html批量梯度下降是最原始的，一次性采用所有数据。它可以很好的代表样本的总体分布，但是训练速度很慢；随机梯度下降是一次用一个样本，它大大加快了训练的速度，但是可能导致局部最优问题并且不易于并行计算；小批量梯度下降则是一次采用batch_size个样本进行训练，可以采用矩阵运算加快训练速度

输出层

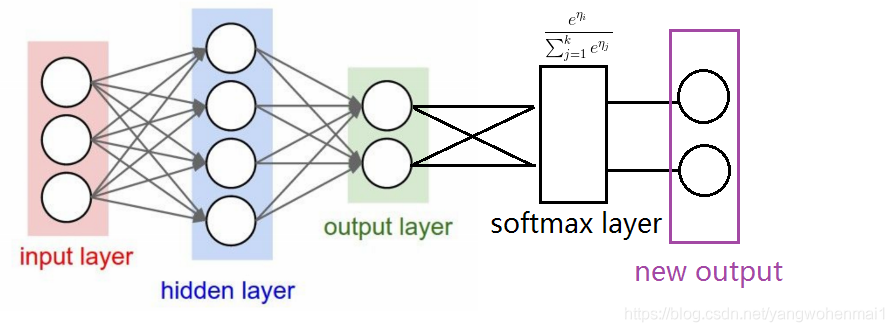
输出层其实就是最后一个隐藏层的输出，也是一个向量。这个向量具体的大小由任务决定，例如在分类任务中由任务的类别决定输出向量的维度。因此最后一个隐藏层的输出大小就是输出层的大小。但是对于分类问题，在最后一个隐藏层后，还需要接上一个softmax分类器，这个softmax层其实就是把输出结果进行了一次换算，将输出结果用概率的形式表现出来，概率和为1，因为一件事情发生的各种概率和一定为1。