leetcode--11 盛水最多的容器 【双指针C/C++】

原题链接：

11. 盛最多水的容器 - 力扣（LeetCode）

题目解析：

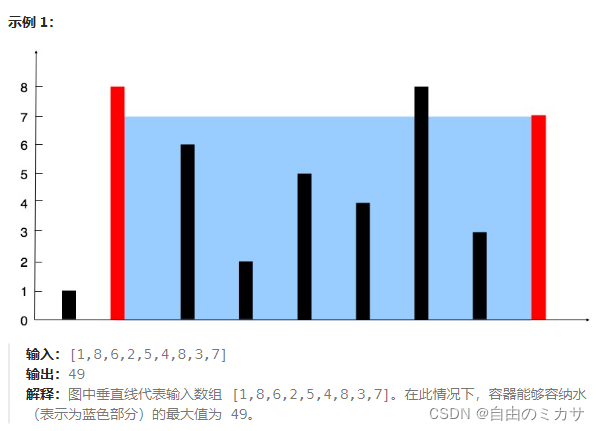
从示例1看，需要返回的最大储水量就是 图中?长x宽（即面积）最大的数 。长是数组下标的差值，以示例1为例，就是两个红色的边的下标的差值；宽就是较矮的那一边的高度。（符合水桶原理，一个水桶的最高水位取决于其最短的板）

算法原理： 单调性+双指针

此题的双指针不是凭空想出来的，而是根据推算，寻找规律，总结出来的。这里为了方便讲述，就直接把左右两端说成左右指针了。实际上，我们是从图中的左右两端的移动? 造成 的容积大小变化而 总结出 左右两端可以看成是双指针的结论。觉得绕的没关系，直接看下面解释。

以 数组 [6， 2 ， 5 ， 4] 为例

定义left 、 right两个指针，指向两端，表示这个储水器的两条边，也可以看成是两块木板。

假设left指向6，right指向4。

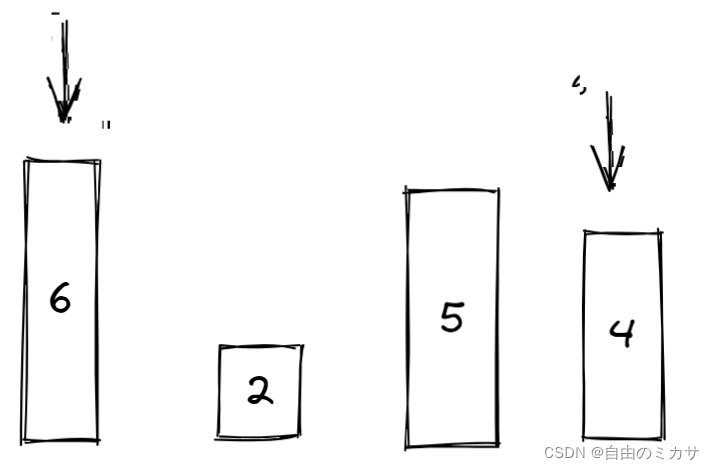
接下来无论移动哪一个指针，其长度都是必然减小的。我们假设指向4的指针不动（即固定较短），移动指向6的指针到2，此时长度和高度都会减小。

若移动left指向5，则right指向的4 作为较矮的那一端，根据水桶原理，其（最短板）高度就是水位的高度，所以就算在宽度减小的时候遇到更高的，其水位高度也不会变化。

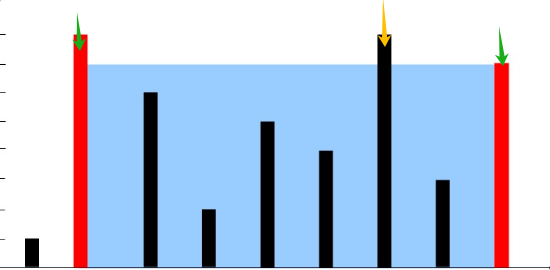
就如图中所示。（黄色箭头表示left移动后的指向）

所以这两种情况下，容积都是变小的。也可以总结成，在固定短板的情况下，无论怎么移动另一块板，容积都变小，也就是盛水的量变小。从这里也可以体现出单调性

------------------------------------------------------------------------------------------------------------------------

而上面的情况都是针对容器的两端中较矮的那一端不动进行研究的，所以继续寻找盛水最多的容器的方法就是移动较矮的那一端。

继续以数组[6， 2 ， 5 ， 4]为例

继续寻找盛水最多的容器的方法就是移动指向4的指针（或者说改变较矮的木板），即不再去遍历计算 固定4（较短板）的容器储水量大小。而是改为以5为端点（移动较短那一端的指针）。

以此类推，直到左右两个指针相遇，结束遍历。

时间复杂度O(n) 空间复杂度O(1)

编写代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int left = 0,right =n-1, ret = 0;
        while(left != right)
        {
            int v = min(height[left],height[right])*(right-left);
            ret= max(ret , v);
            if(height[left] > height[right])
            {
                right--;
            }
            else
            {
                left++;
            }
        }
        return ret;
    }
};