数据库 补充 树,红黑树,b树,b+树
01.树

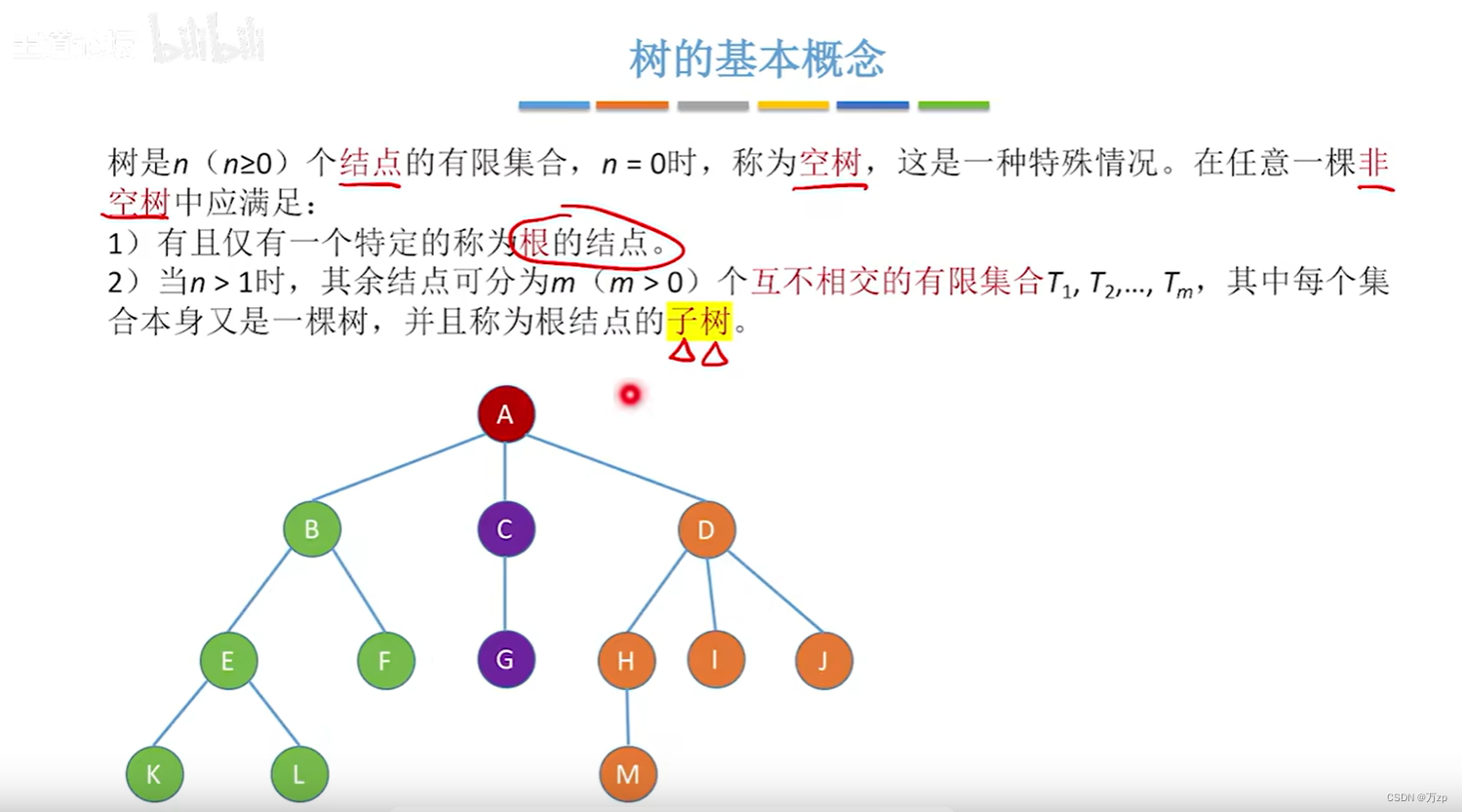
02.二叉树和二叉平衡树
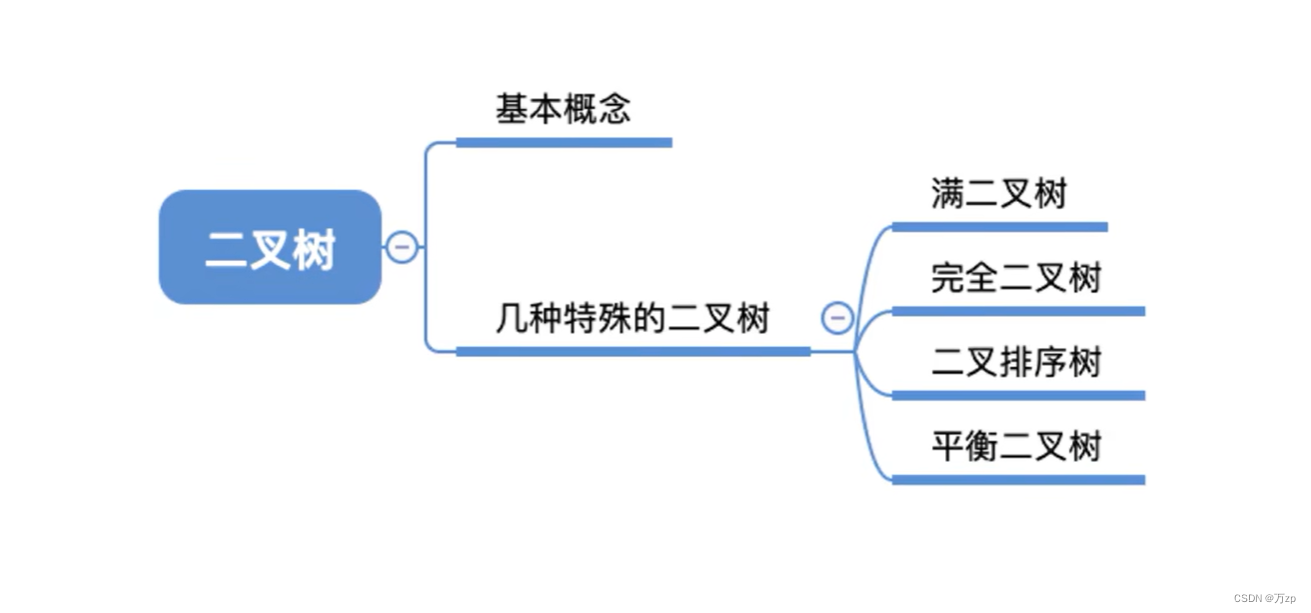
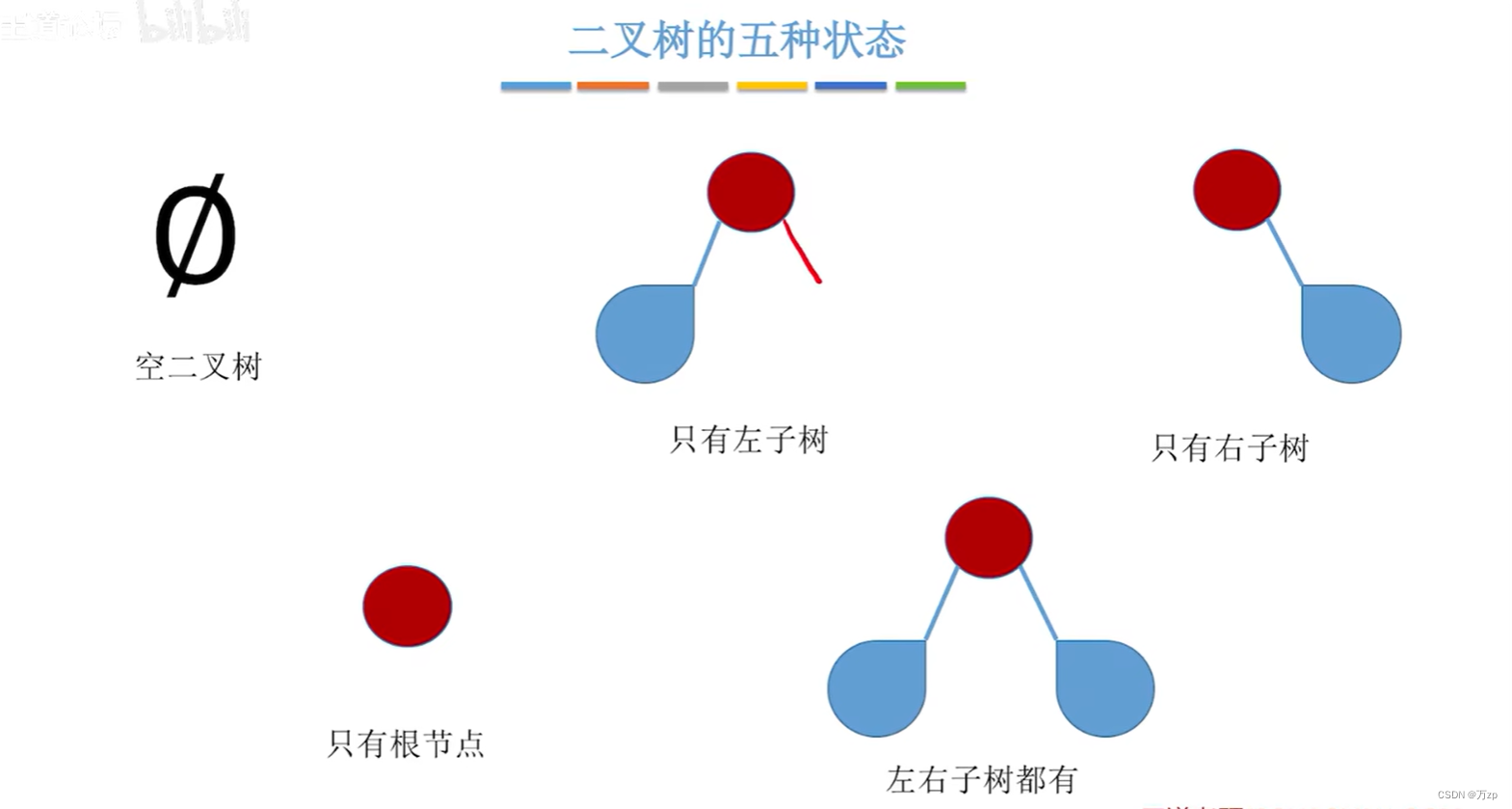
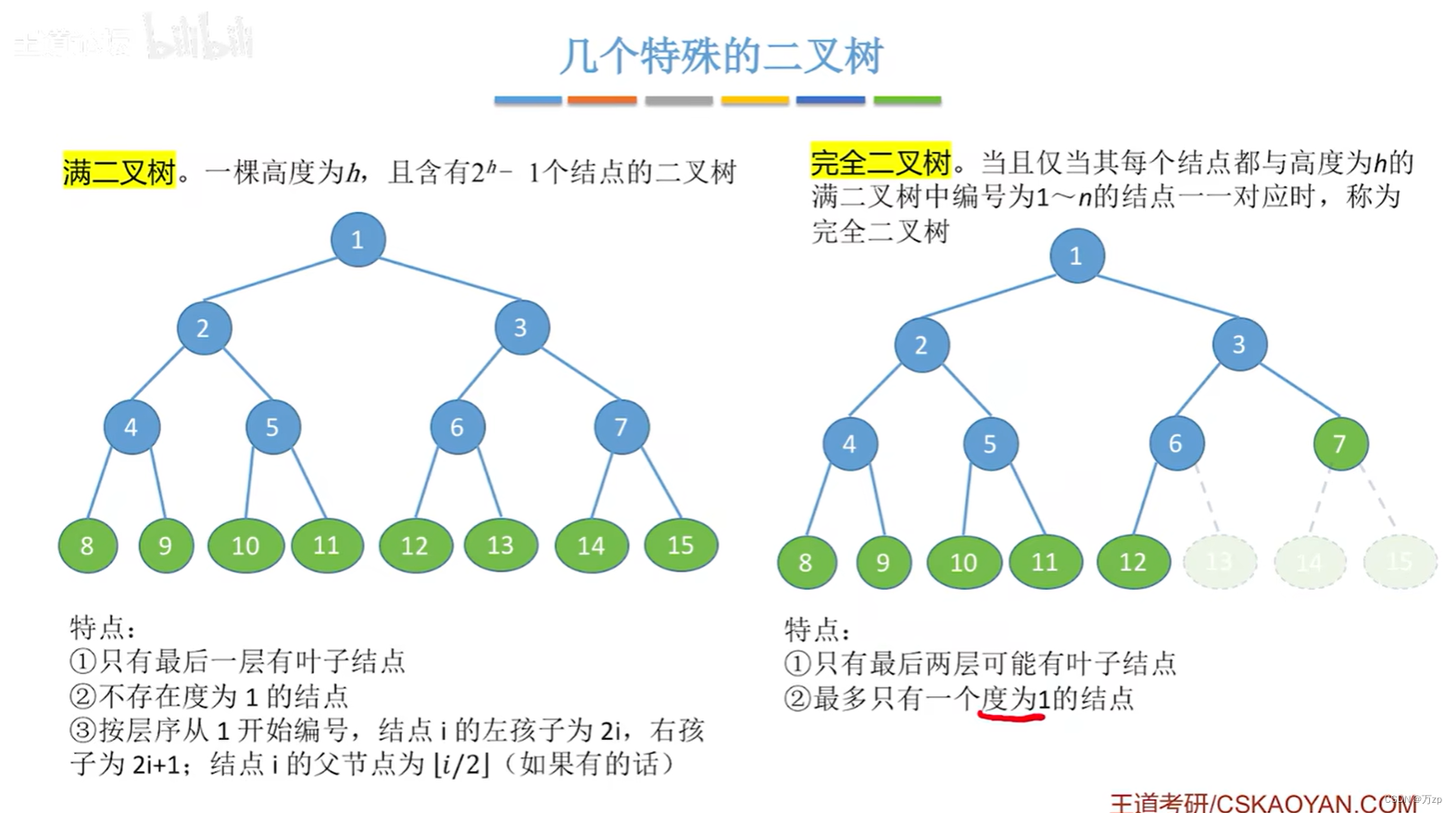
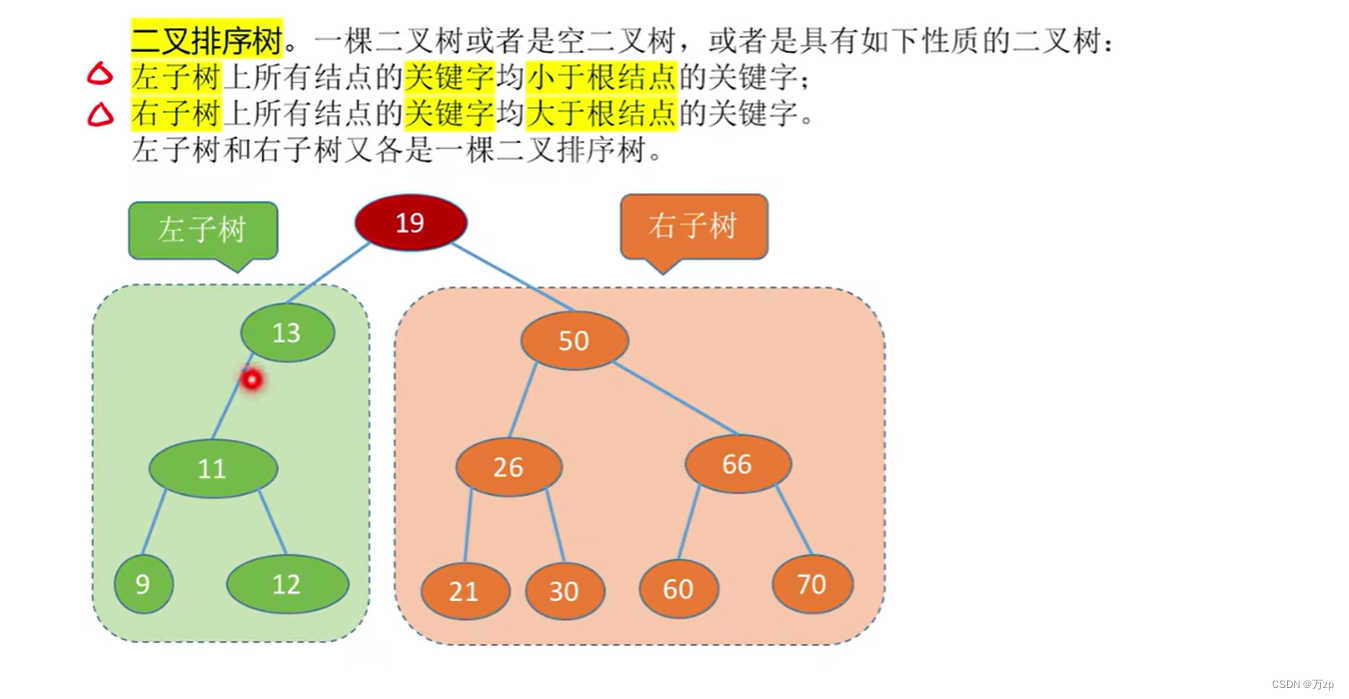
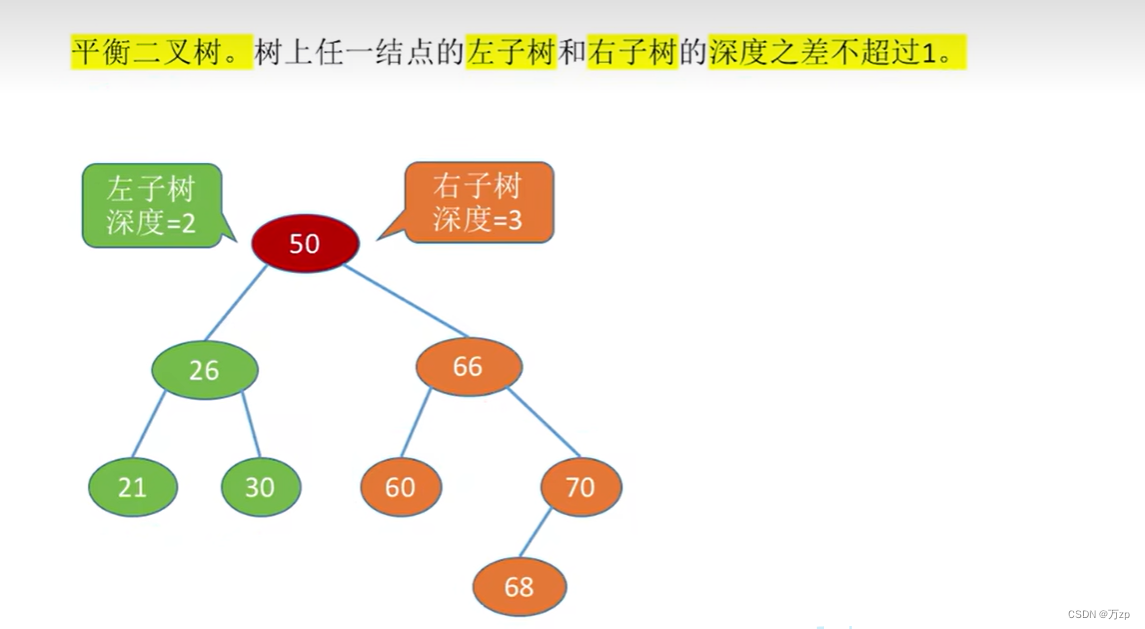
03.平衡二叉树的恢复

将导致不平衡的结点称作被破坏者,破坏了结点的平衡的结点成为破坏者,经过调整可以让该树平衡的结点称为调整结点。
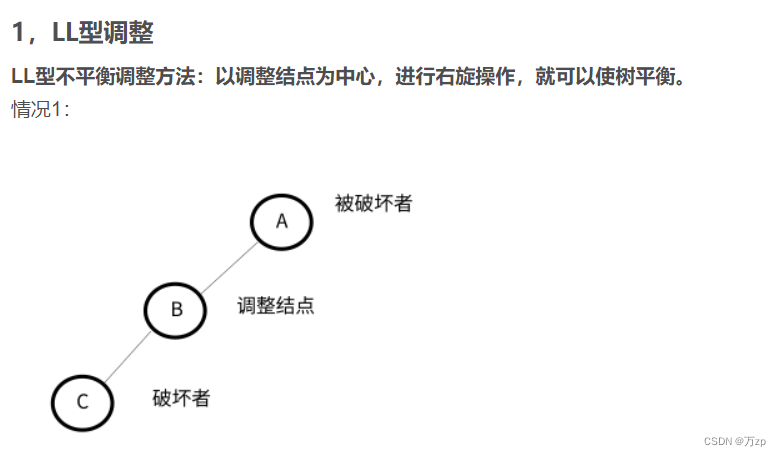
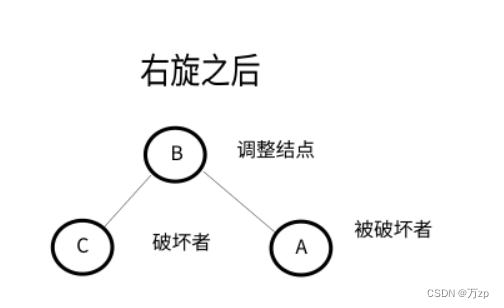
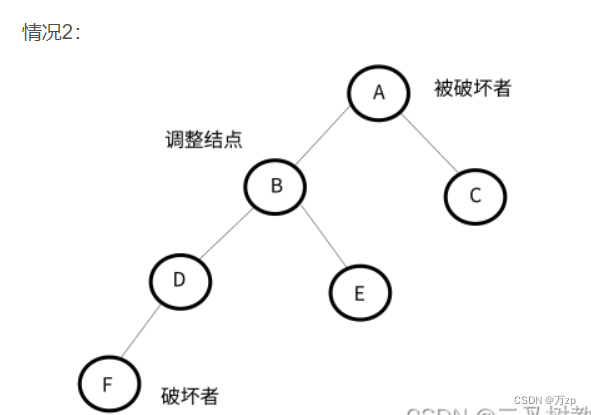
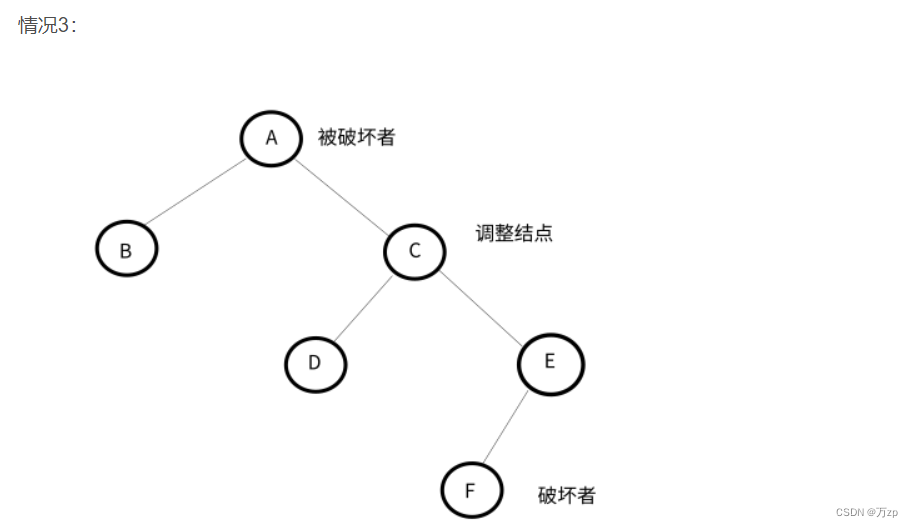
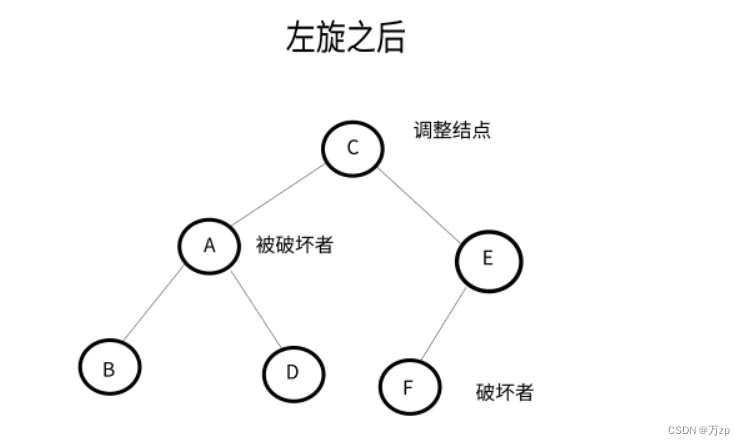

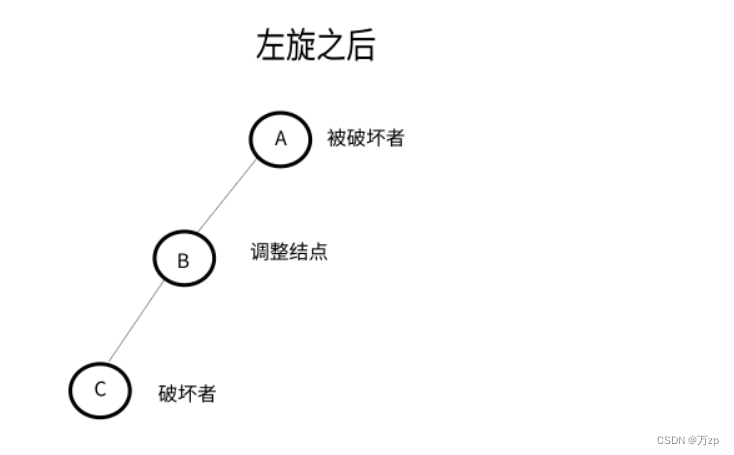



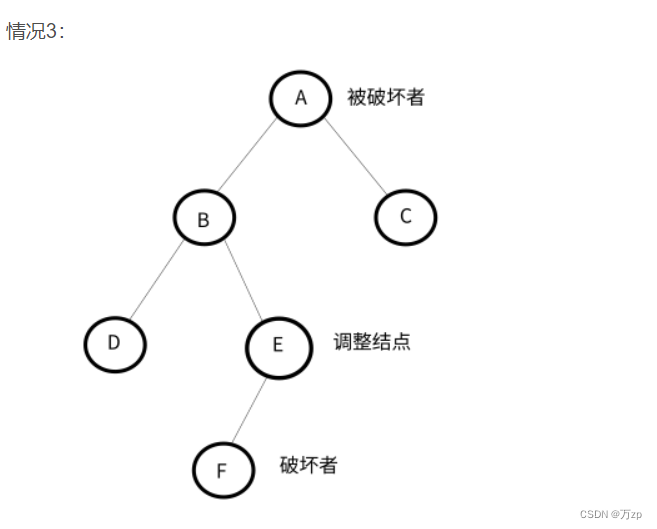


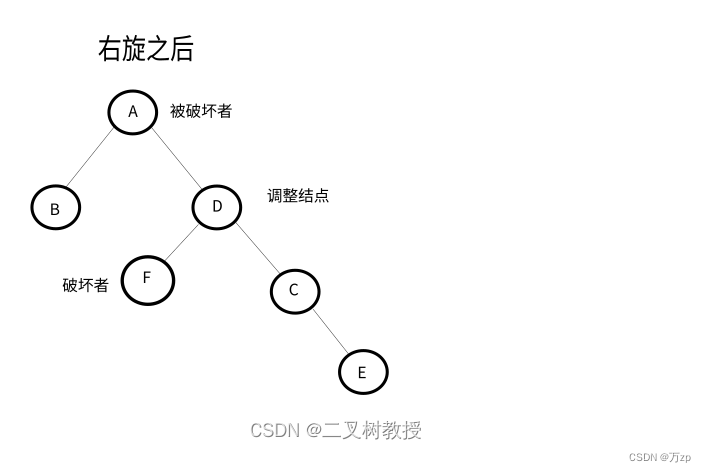
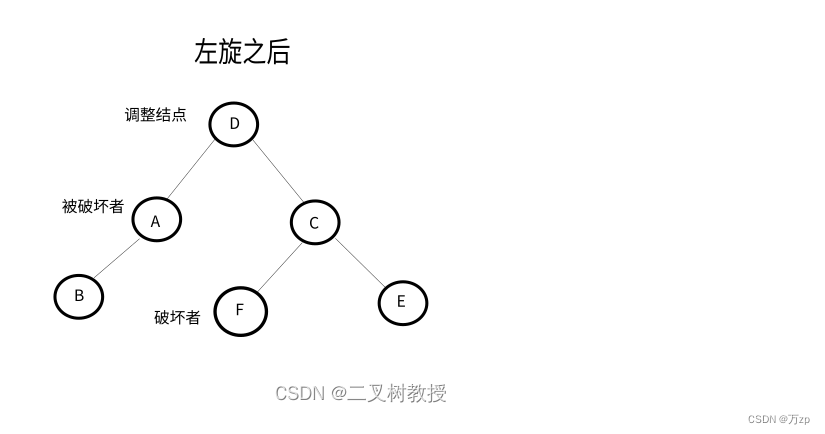
LL型:
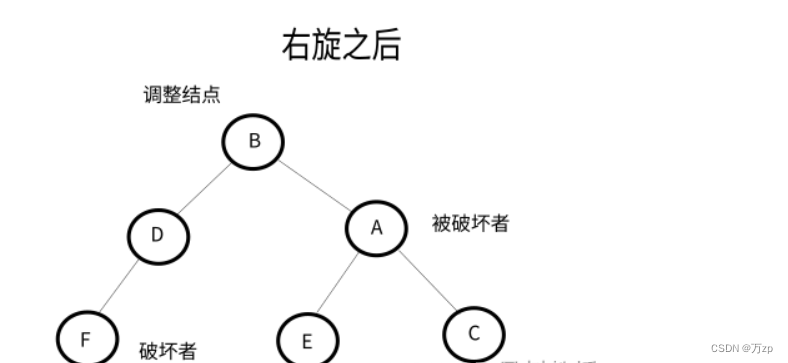
以被破坏者的左孩子结点作为调整结点,对其进行右旋。如果调整结点有右子树,将其右子树作为被破坏者的左子树。
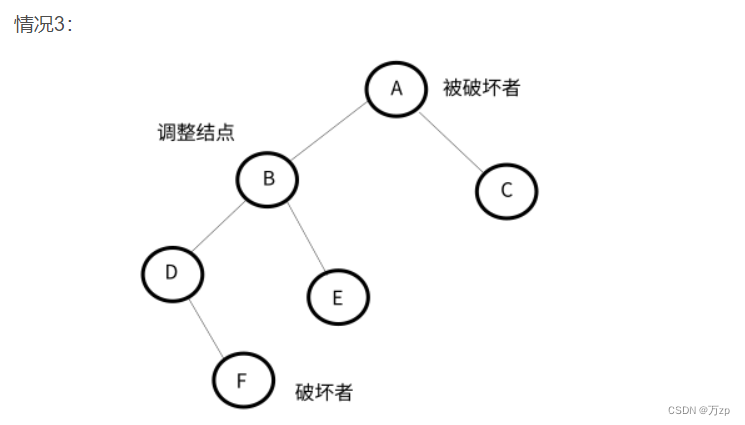
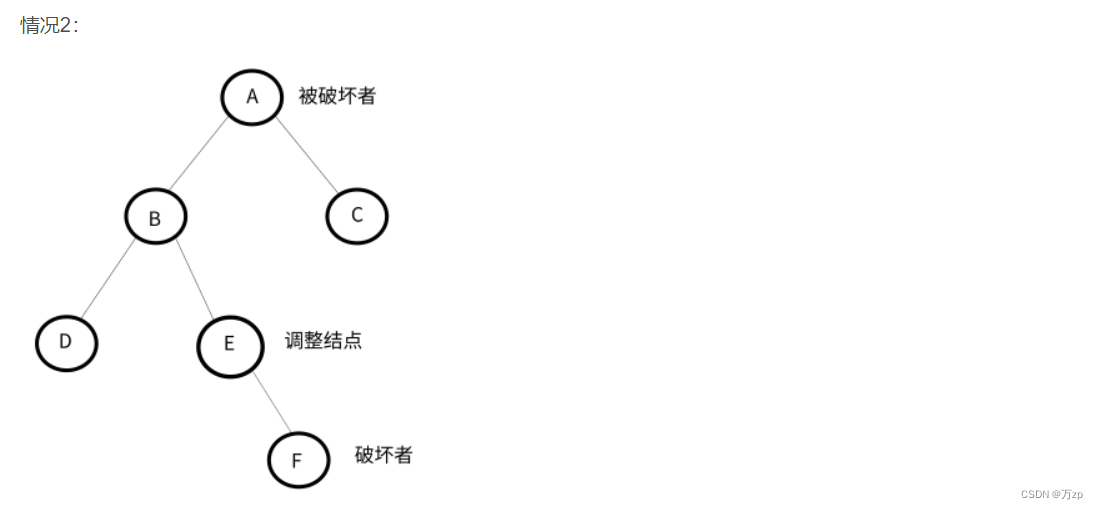
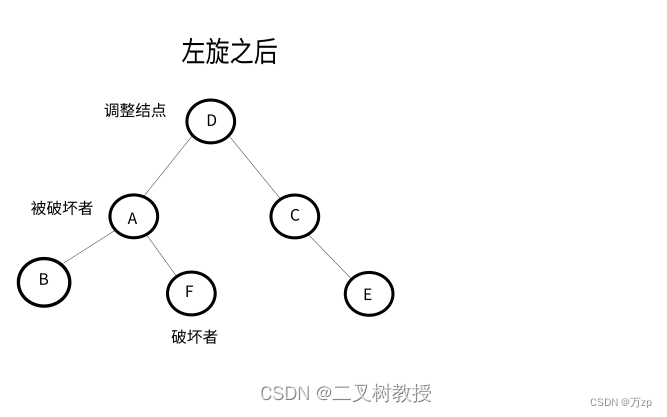
LR型:
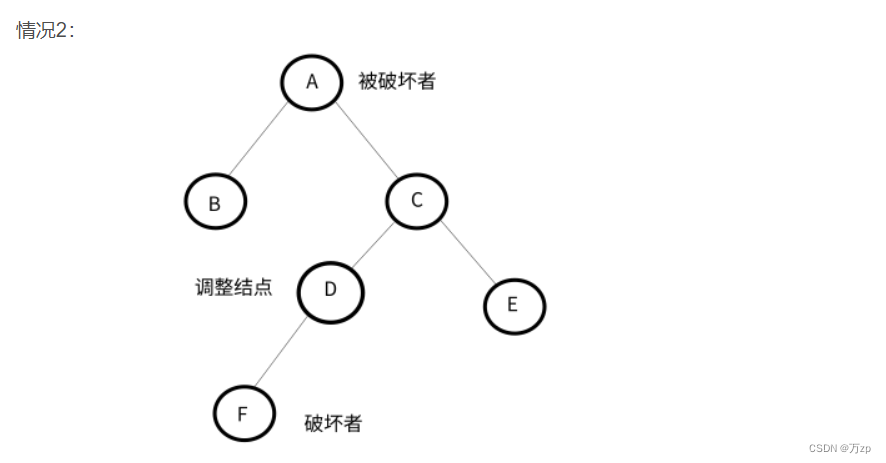
以被破坏者的左孩子的右孩子结点为调整结点。
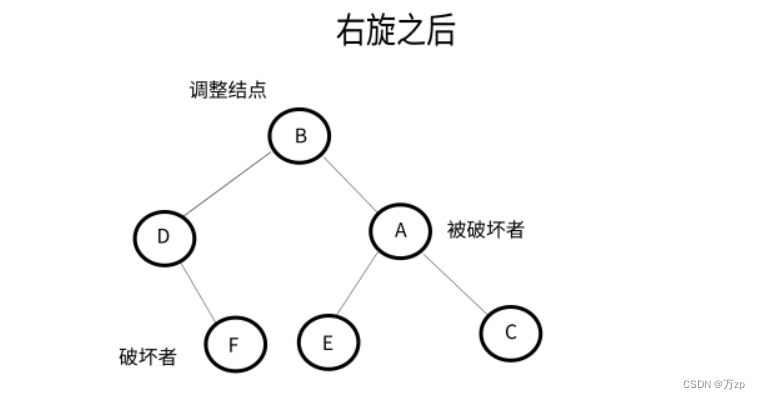
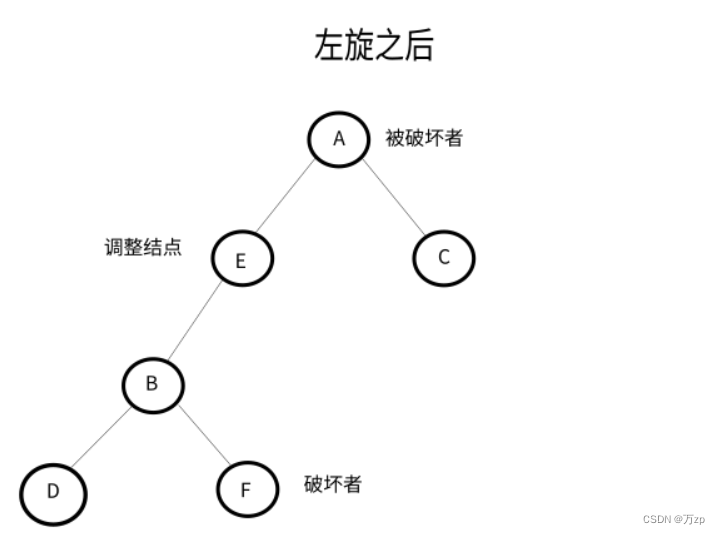
如果破坏者为调整结点的左孩子,以调整结点进行左旋,将破坏者作为调整结点的父节点的右子树,后进行右旋,破坏者位置保持不变。
如果破坏者为调整结点的右孩子,以调整结点进行左旋,破坏者位置保持不变。后进行右旋,将破坏者作为被破坏者的左子树。
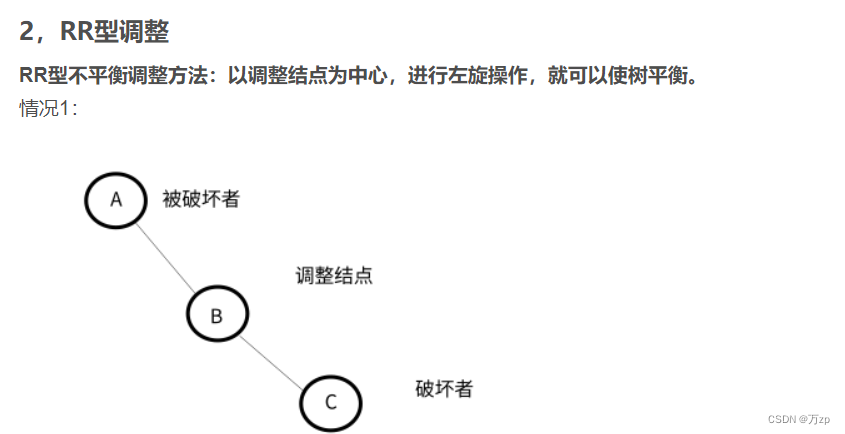
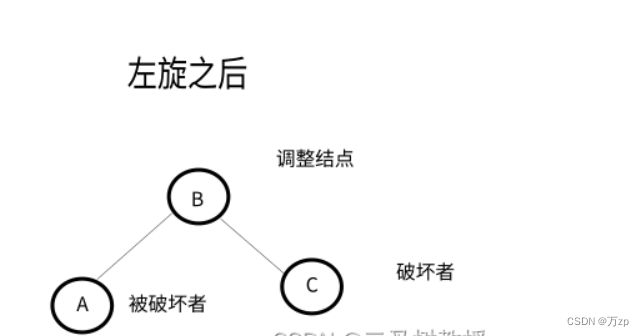
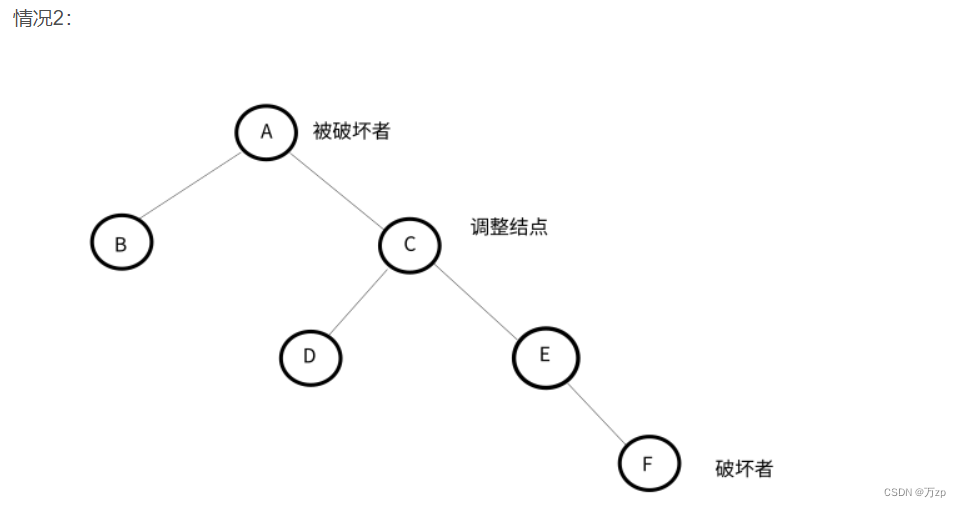
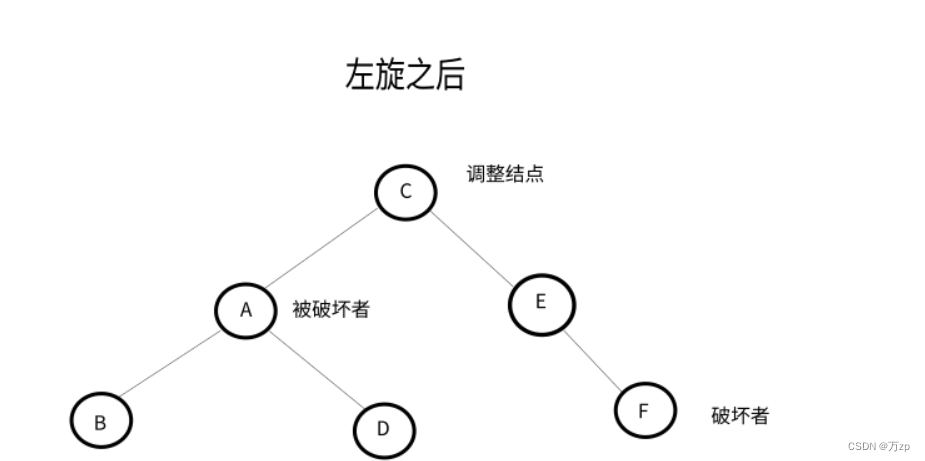
RR型:
以被破坏者的右孩子结点为调整结点,对其进行左旋。如果调整结点有左子树,将其右子树作为被破坏者的右子树。
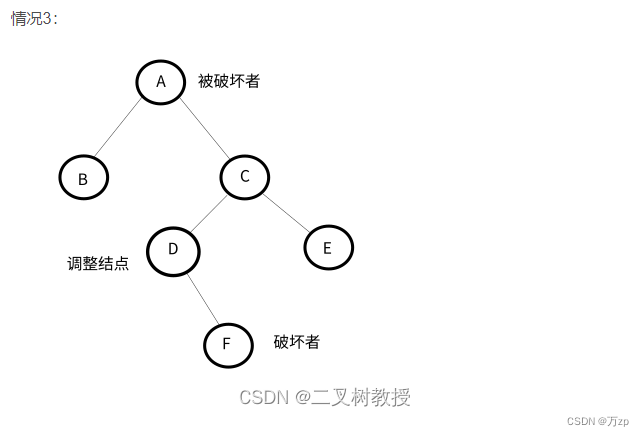
RL型:
以被破坏者的右孩子的左孩子结点为调整结点。
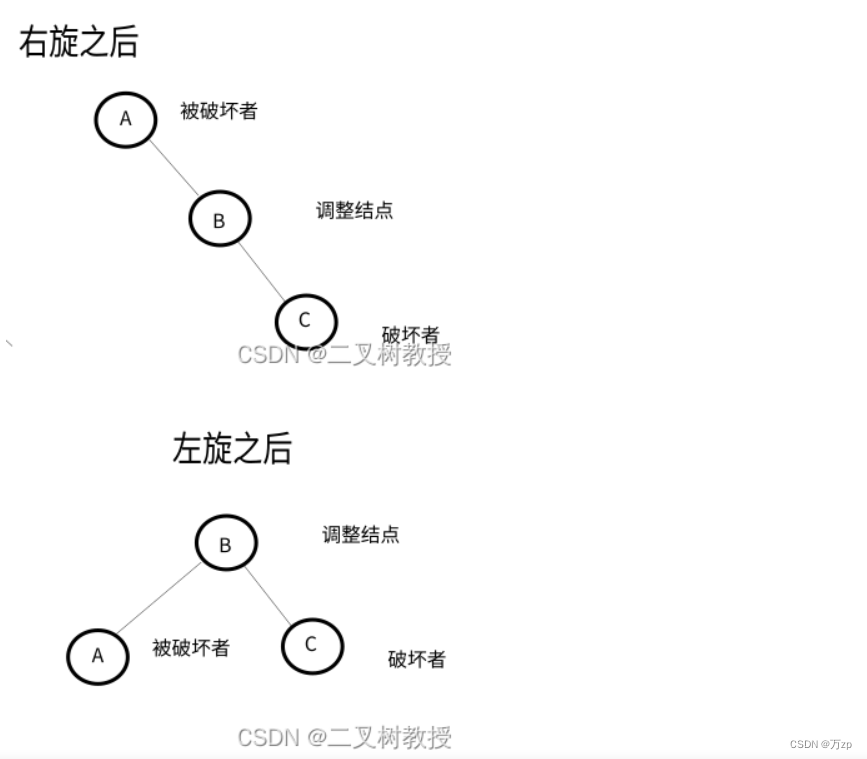
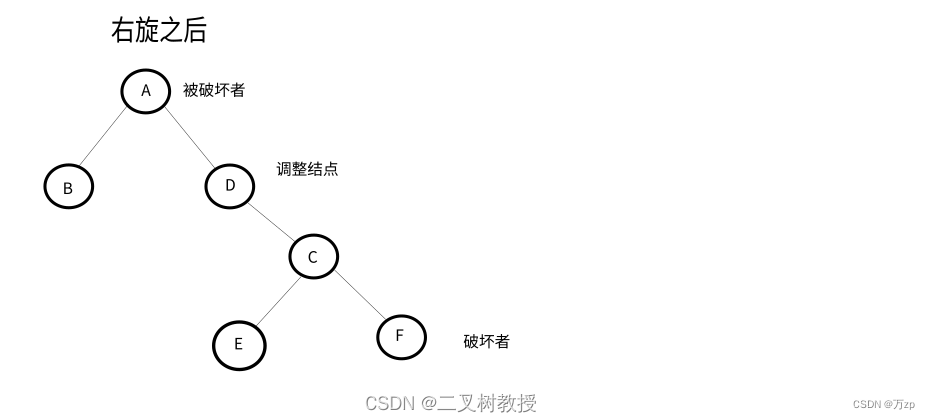
如果破坏者为调整结点的左孩子,以调整结点进行右旋,破坏者位置保持不变,后进行左旋,将破坏者作为被破坏者的右子树。
如果破坏者为调整结点的右孩子,以调整结点进行右旋,将破坏者作为调整结点的父节点的左子树。后进行左旋,破坏者位置保持不变。
红黑树:
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。
http://t.csdnimg.cn/Gy3MM
最重要的是红黑树的根节点到任意的叶子结点的最短路径都是一样的长度。
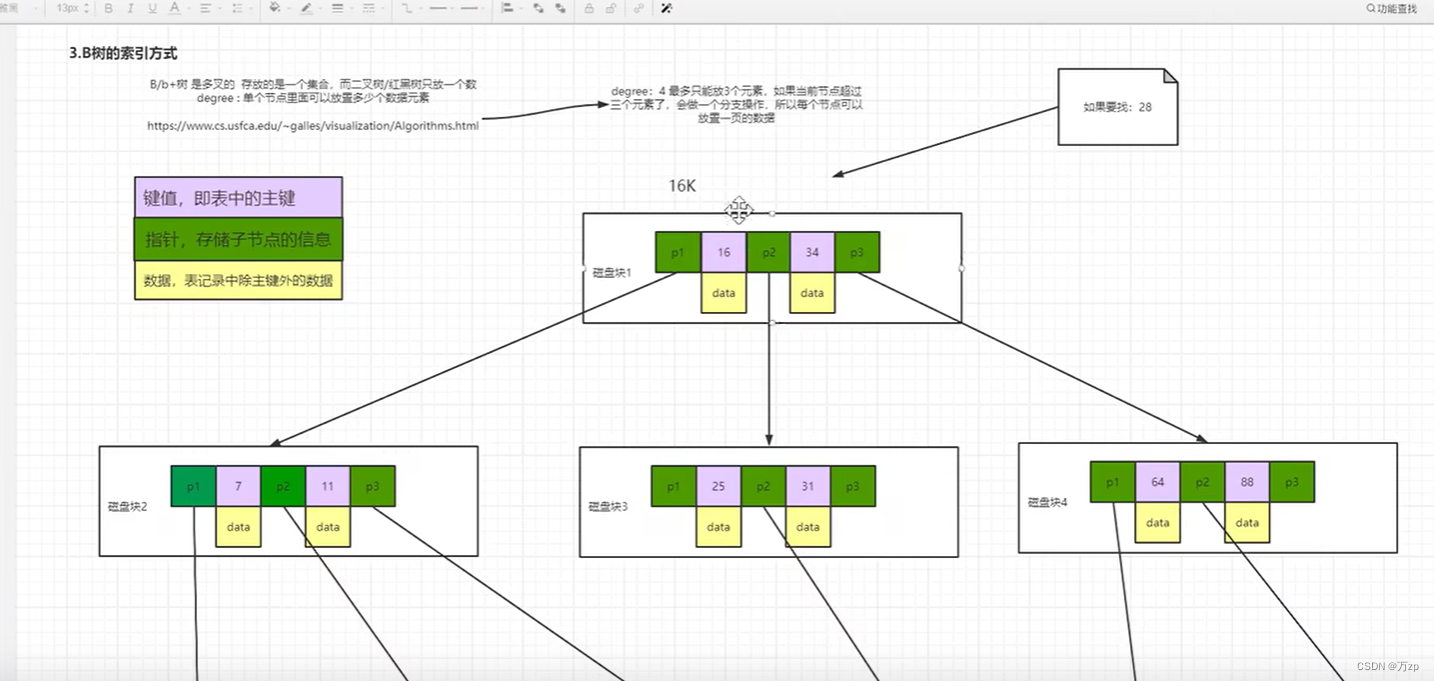
B树:(m阶查找树)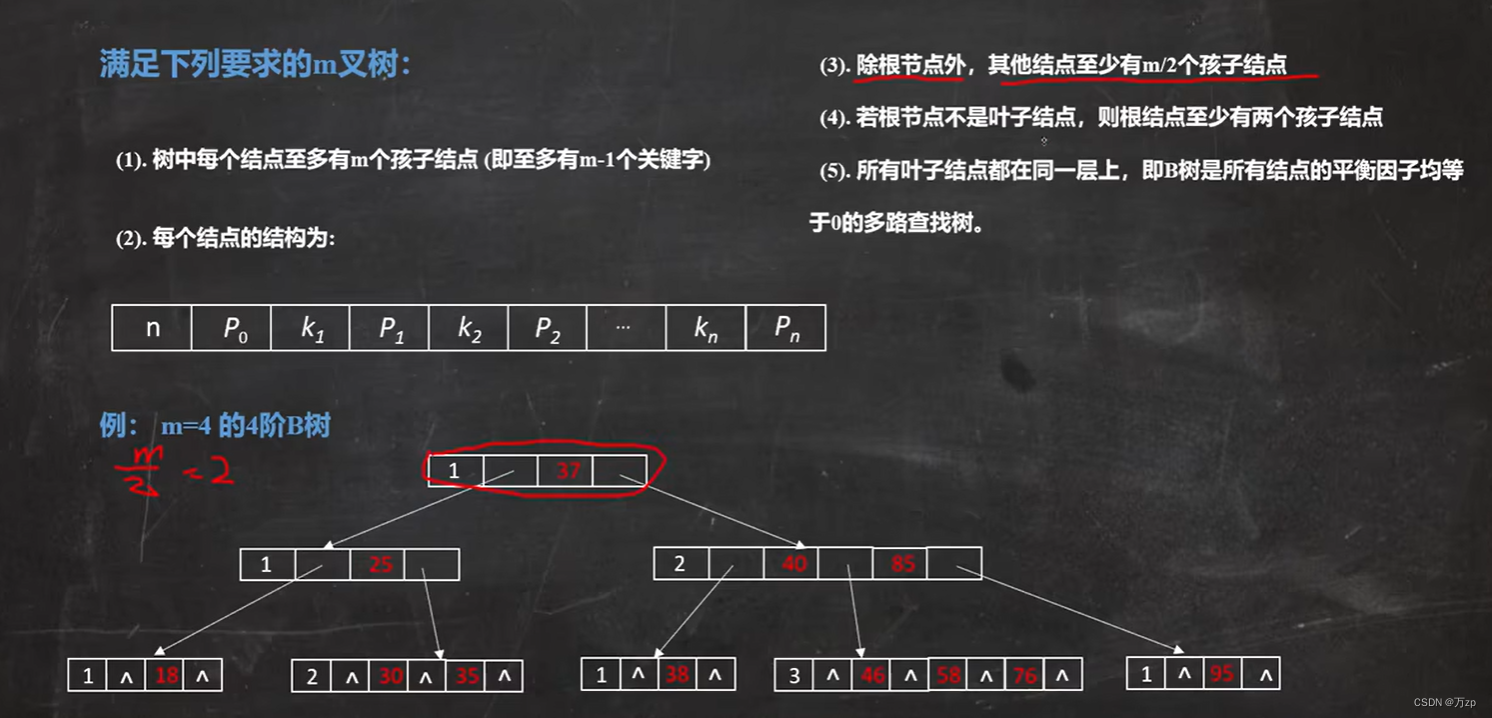
节点结构中的
n记录关键字的个数
k是关键字
p是指针
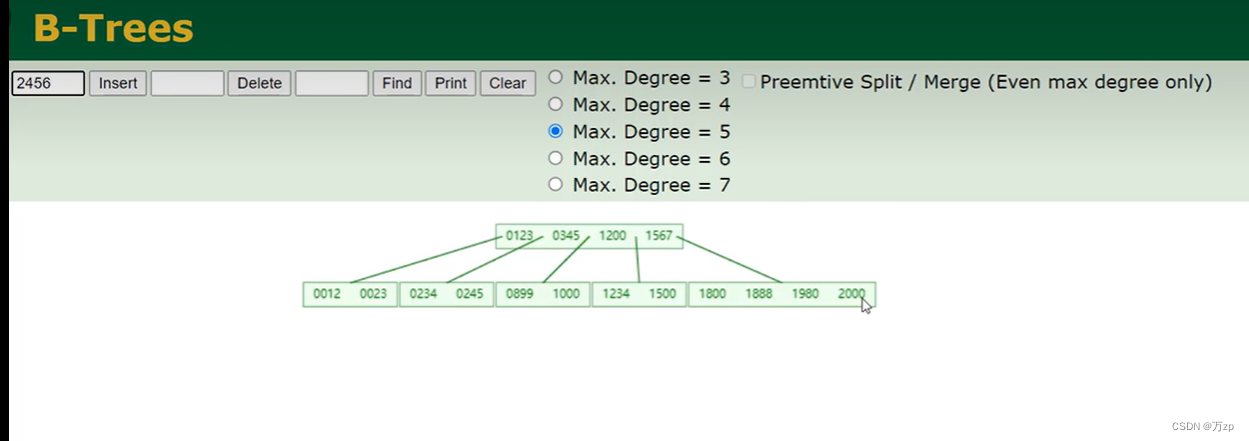
一颗m阶的B树满足如下条件:
- 每个节点最多只有m个子节点(节点内至多m-1关键字)。
- 除根节点外,每个非叶子节点具有至少有 m/2(向下取整)个子节点。
- 非叶子节点的根节点至少有两个子节点。
- 有k颗子树(k个孩子节点)的非叶节点有k-1个键,键按照递增顺序排列。 叶节点都在同一层中。
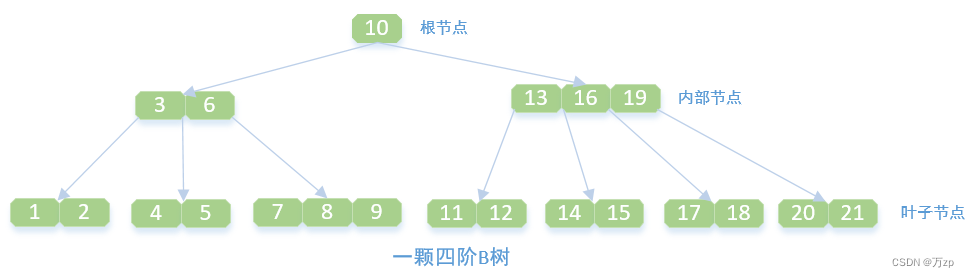
(1)什么是B树的阶 ?
B树中一个节点的子节点数目的最大值,用m表示,假如最大值为4,则为4阶,如图,所有节点中,节点[13,16,19]拥有的子节点数目最多,四个子节点(灰色节点),所以可以定义上面的图片为4阶B树。
(2)什么是根节点 ?
节点【10】即为根节点,特征:根节点拥有的子节点数量的上限和内部节点相同,如果根节点不是树中唯一节点的话,至少有俩个子节点(不然就变成单支了)。在m阶B树中(根节点非树中唯一节点),那么有关系式2<= M <=m,M为子节点数量;包含的元素数量 1<= K <=m-1,K为元素数量。
(3)什么是内部节点 ?
节点【13,16,19】、节点【3,6】都为内部节点,特征:内部节点是除叶子节点和根节点之外的所有节点,拥有父节点和子节点。假定m阶B树的内部节点的子节点数量为M,则一定要符合(m/2)<= M <=m关系式,包含元素数量M-1;包含的元素数量 (m/2)-1<= K <=m-1,K为元素数量。m/2向上取整。
(4)什么是叶子节点?
节点【1,2】、节点【11,12】等最后一层都为叶子节点,叶子节点对元素的数量有相同的限制,但是没有子节点,也没有指向子节点的指针。特征:在m阶B树中叶子节点的元素符合(m/2)-1<= K <=m-1。
b树的形成:
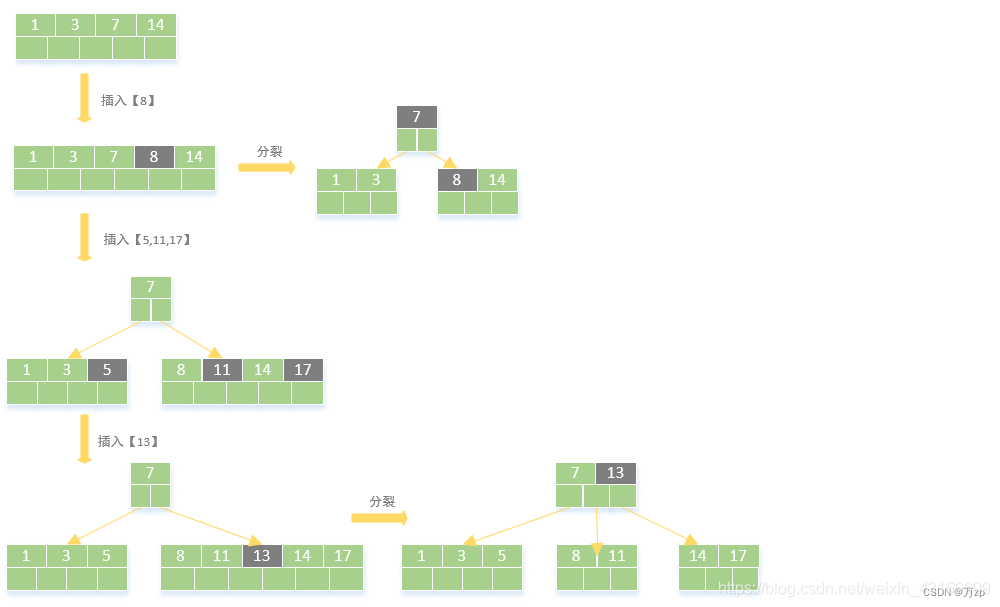
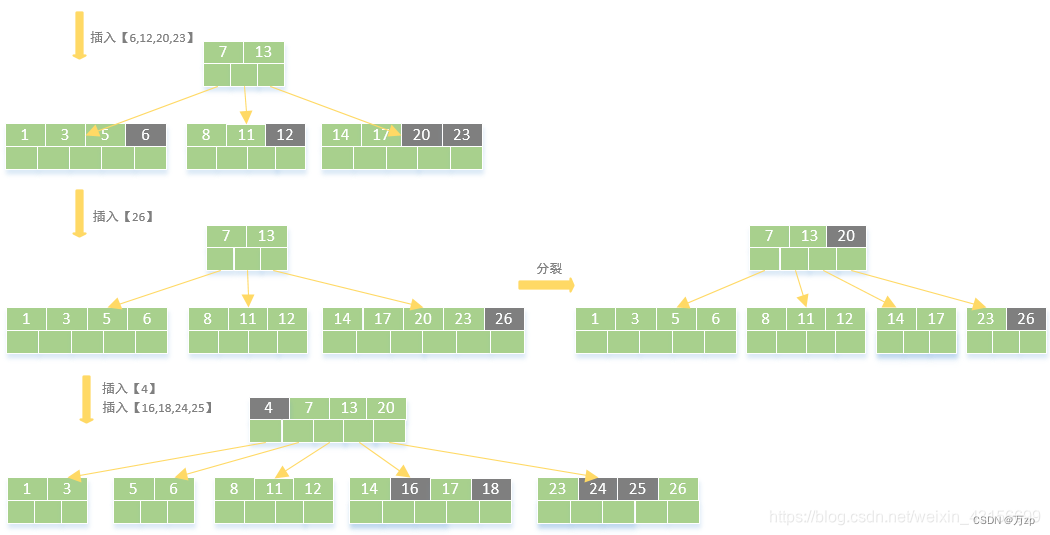
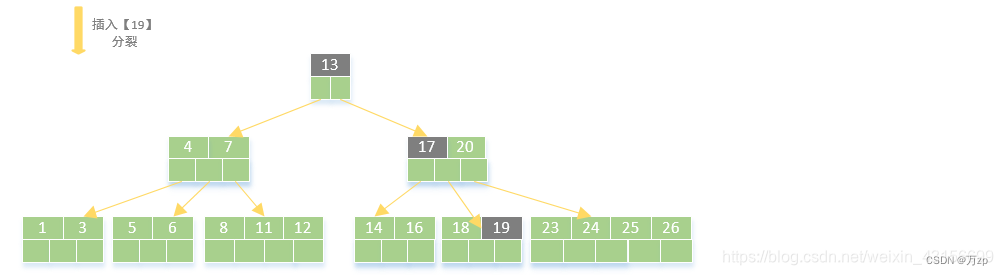
b+树:
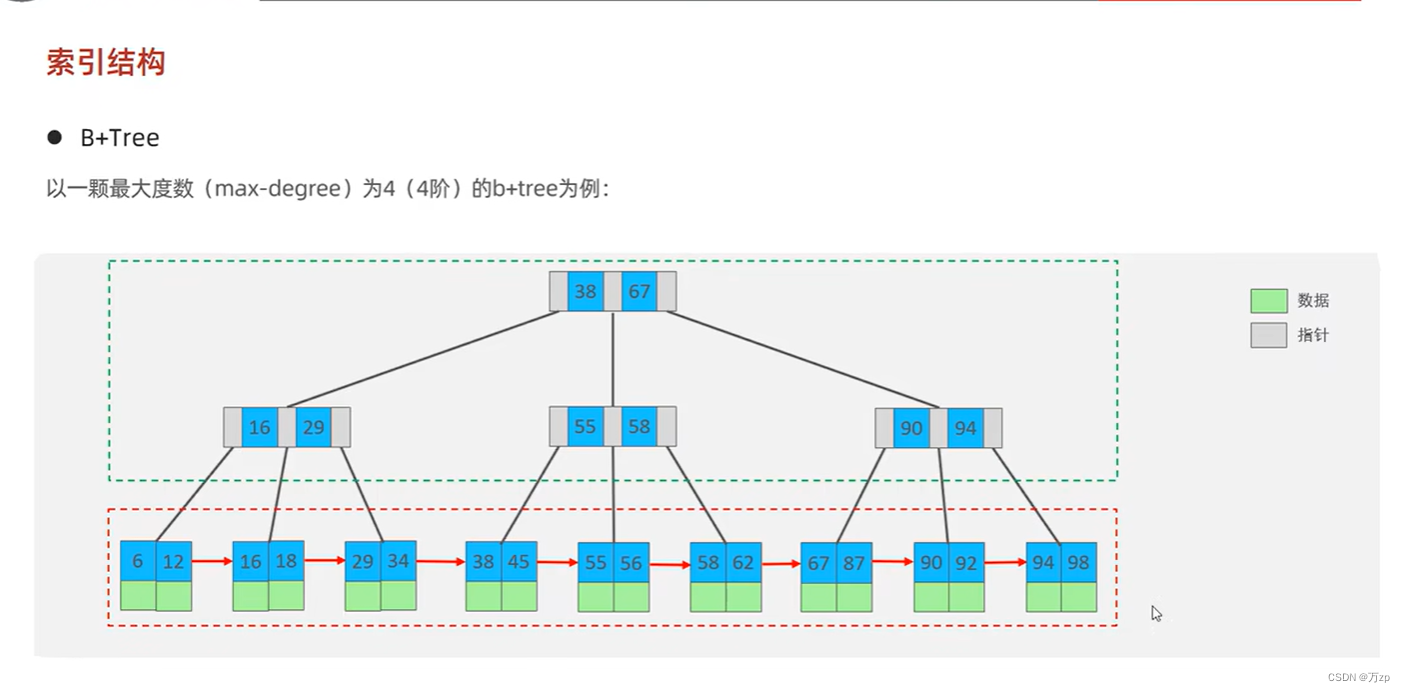
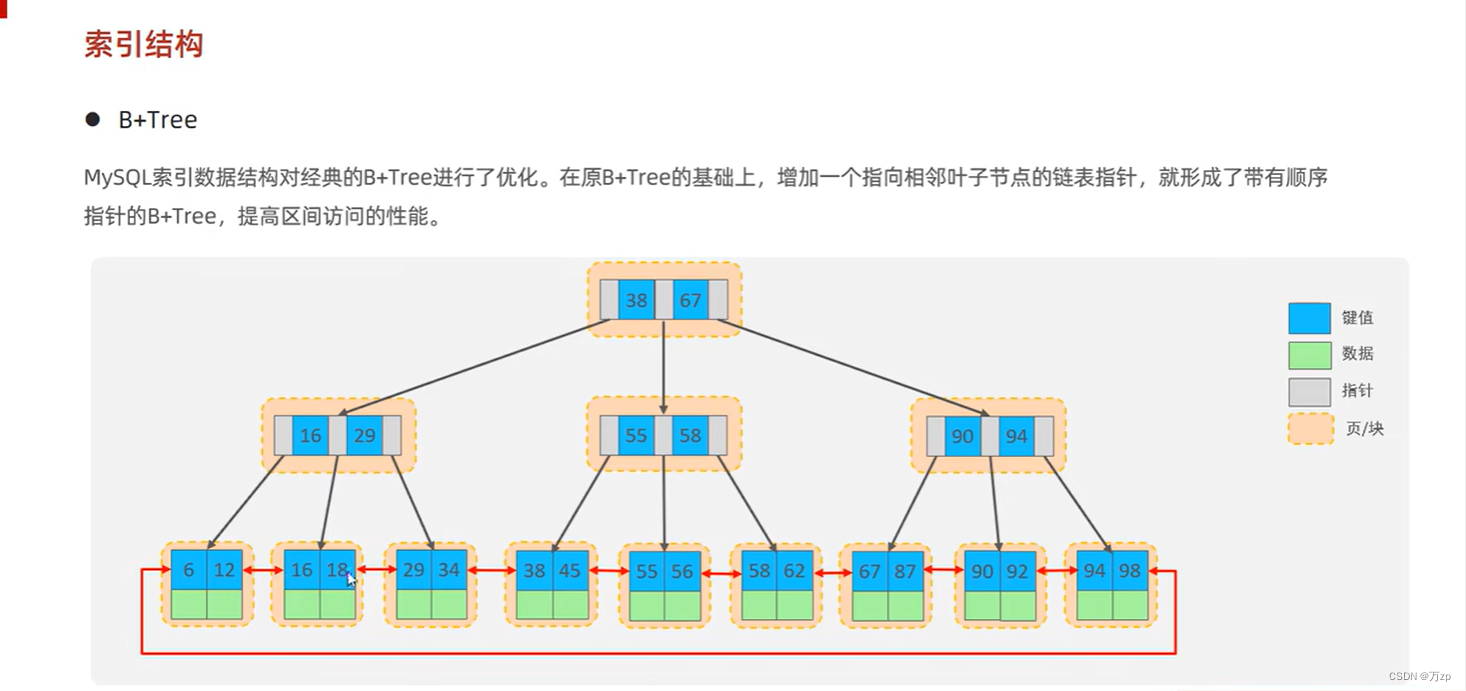
所有节点都会出现在叶子节点链表中:
叶子节点会形成一个链表。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!