第二课:布尔逻辑与逻辑门、二进制及算术逻辑单元
2023-12-28 10:41:30
第二课:布尔逻辑与逻辑门、二进制及算术逻辑单元
各位小伙伴想要博客相关资料的话,关注公众号:chuanyeTry即可领取相关资料!
第三章:布尔逻辑与逻辑门
1、计算机为什么使用二进制
- 计算机的元器件晶体管只有 2 种状态,通电(1)&断电(0),用二进制可直接根据元器件的状态来设计计算机。
- 而且,数学中的“布尔代数”分支,可以用 True 和 False(可用 1 代表 True,0 代表 False)进行逻辑运算,代替实数进行计算。
- 计算的状态越多,信号越容易混淆,影响计算。对于当时每秒运算百万次以上的晶体管,信号混淆是特别让人头疼的。
2、布尔代数&布尔代数在计算机中的实现
- 变量:没有常数,仅 True 和 False 这两个变量。
- 三个基本操作:NOT/AND/OR。
- 为什么称之为“门”:控制电流流过的路径
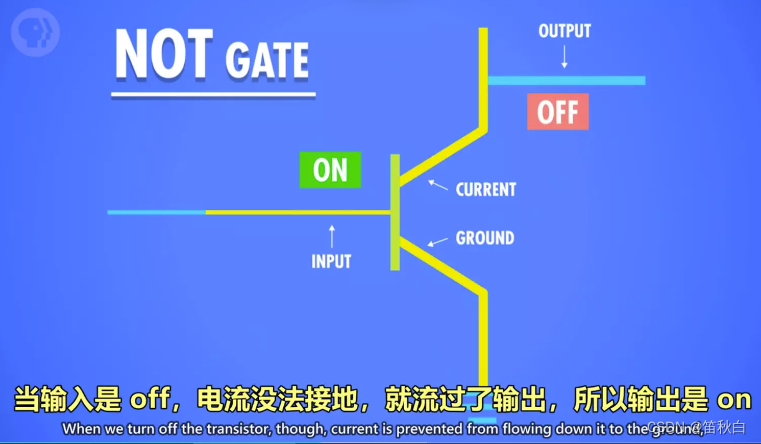
1)NOT 操作
- 命名:称为 NOT 门/非门。
- 作用:将输入布尔值反转。输入的 True 或 False,输出为 False 或 True。
- 晶体管的实现方式:
– 半导体通电 True,则线路接地,无输出电流,为 False。
– 半导体不通电 False,则输出电流从右边输出,为 True。
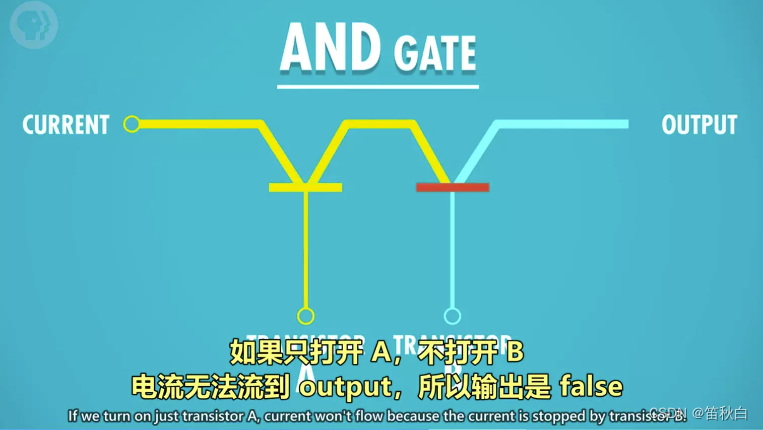
2)AND 操作
- 命名:AND 门/与门
- 作用:由 2 个输入控制输出,仅当 2 个输入 input1 和 input2 都为 True 时,输出才为 True,2 个输入的其余情况,输出均为 False。
可以理解为,2 句话(输入)完全没有假的,整件事(输出)才是真的。

- 用晶体管实现的方式:串联两个晶体管,仅当 2 个晶体管都通电,输出才有电流(True)。
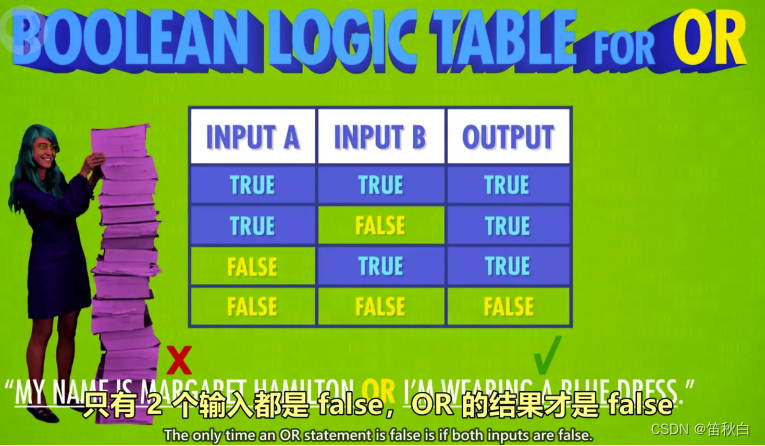
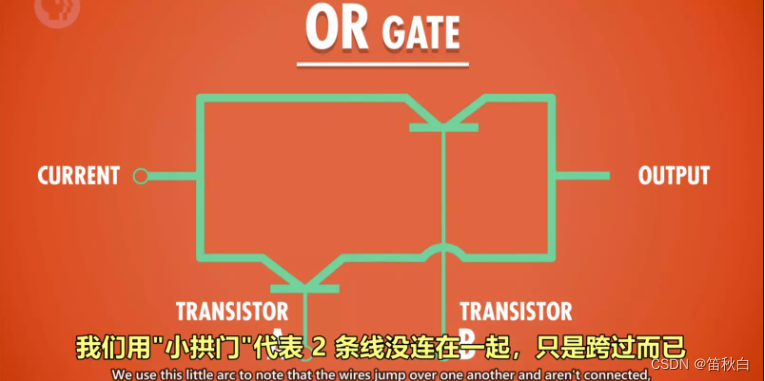
3)OR 操作
- 命名:OR 门/或门
- 作用:由 2 个输入控制输出,只要其中一个输入为 True,则输出 True。
- 用晶体管实现的方式:使用 2 个晶体管,将它们并联到电路中,只要有一个晶体管通电,则输出有电流(True)。
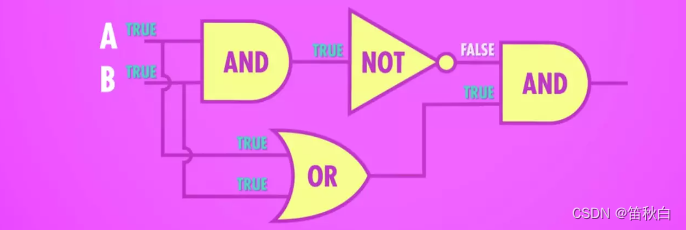
3、特殊的逻辑运算——异或
- 命名:XOR 门/异或门
- 作用:2 个输入控制一个输出。当 2 个输入均为 True 时,输出 False,其余情况与 OR 门相同。

- 图示:先用一个 OR 门,将其与 AND 门并联,AND 门与 NOT 门串联,最后让 NOT 与 AND 门并联,获得输出。
4、逻辑门的符号表示
- 作用:将逻辑门简化,将逻辑门用于构建更大的组件,而不至于太复杂。
- 图示:

– 非门:用三角形+圆圈表示
– 与门:用 D 型图案表示
– 或门:用类似 D 向右弯曲的图案表示
– 异或门:用或门+一个圆弧表示
5、抽象的好处
使得分工明确,不同职业的工程师各司其职,而不用担心其他细节。
第四章:二进制
1、二进制的原理,存储单元 MB/GB/TB 解释
- 计算机中的二进制表示:单个数字 1 或 0,1 位二进制数字命名为位(bit),也称 1 比特。
- 字节(byte)的概念:1byte=8bit,即 1byte 代表 8 位数字。最早期的电脑为八位的,即以八位为单位处理数据。为了方便,将八位数字命名为 1 字节(1byte).
- 十进制与二进制的区别:
– 十进制有 10 个数字,0-9,逢 10 进 1(不存在 10 这个数字),则每向左进一位,数字大 10 倍。
– 二进制有 2 个数字,0-1,逢 2 进 1,(不存在 2 这个数字),则每向左进一位,数字大 2 倍。 - 如何进行二进制与十进制联系起来:
– 将十进制与二进制的位数提取出来,编上单位:
eg.二进制的 1011=1* 2^0 + 1* 2^1 + 0* 2^2 + 1* 2^3= 11(从右往左数)
eg.十进制的 1045= 1* 10^3 + 0* 10^2 + 4* 10^1 + 5* 10^0 - 十进制与二进制的图示:
十进制的 263

二进制的 10110111
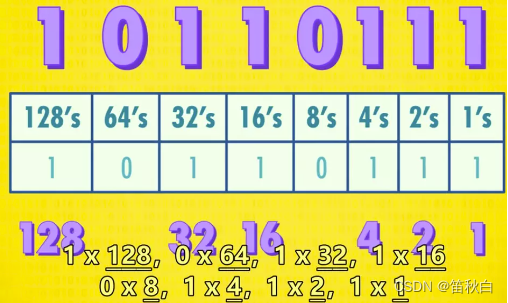
- 二进制的运算:
相同的位数相加,逢 2 进 1

- byte 在电脑中的单位换算:
1kb=2^10bit = 1024byte =1000b
1TB=1000GB
1GB=十亿字节=1000MB=10^6KB - 32 位与 64 位电脑的区别
32 位的最大数为 43 亿左右 32 位能表示的数字:0——2的32次方-1,一共2的32次方个数
64 位的最大数为 9.2*10^18
2、正数、负数、正数、浮点数的表示
1)计算机中表示数字的方法
- 整数:
表示方法:
– 第 1 位:表示正负 1 是负,0 是正(补码)
– 其余 31 位/63 位: 表示实数 - 浮点数(Floating Point Numbers):
定义:小数点可在数字间浮动的数(非整数)
表示方法:IEEE 754 标准下用类似科学计数法的方式,存储十进制数值
– 浮点数=有效位数*指数
– 32 位数字中:第 1 位表示正负,第 2-9 位存指数。剩下 23 位存有效位数eg.625.9=0.6259(有效位数)*10^3(指数)
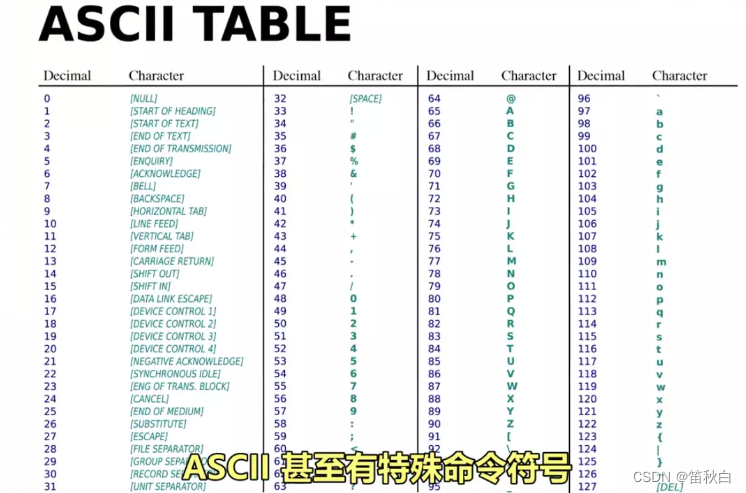
3、美国信息交换标准代码-ASCⅡ,用来表示字符
- 全称:美国信息交换标准代码
- 作用:用数字给英文字母及符号编号
- 内容:7 位代码,可存放 128 个不同的值。
- 图示:
4、UNICODE,统一所有字符编码的标准
- 诞生背景:1992 诞生,随着计算机在亚洲兴起,需要解决 ASCⅡ不够表达所有语言的问题。为提高代码的互用性,而诞生的编码标准。
- 内容:UNICODE 为 17 组的 16 位数字,有超过 100 万个位置,可满足所有语言的字符需求。
第五章:算术逻辑单元
1、什么是算术逻辑单元
- 命名:简称 ALU,Arithmetic&Logic Unit
- 组成:ALU 有 2 个单元,1 个算术单元和 1 个逻辑单元(Arithmetic Unit 和 Logic Unit)
- 作用:计算机中负责运算的组件,处理数字/逻辑运算的最基本单元。
2、算术单元
1)基本组件
- 由半加器、全加器组成
– 半加器、全加器由 AND、OR、NOT、XOR 门组成
2)加法运算
- 组件:AND、OR、NOT、XOR 门
- 元素:输入 A,输入 B,输出(均为 1 个 bit,即 0 或 1)
- 半加器:
- 作用:用于计算个位的数字加减。
– 输入:A,B
– 输出:总和,进位
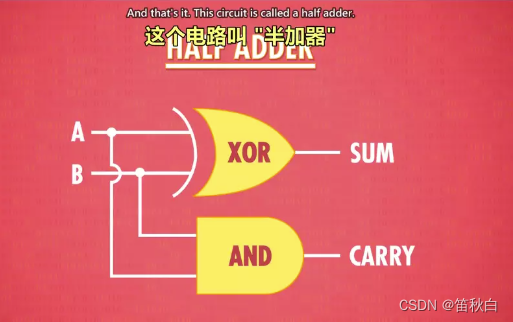
- 抽象:

– sum :总和
– carry:进位
- 全加器:作用:用于计算超过 1 位的加法(ex:1+1+1),由于涉及进位,因此有 3 个输入(C 充当进位)。
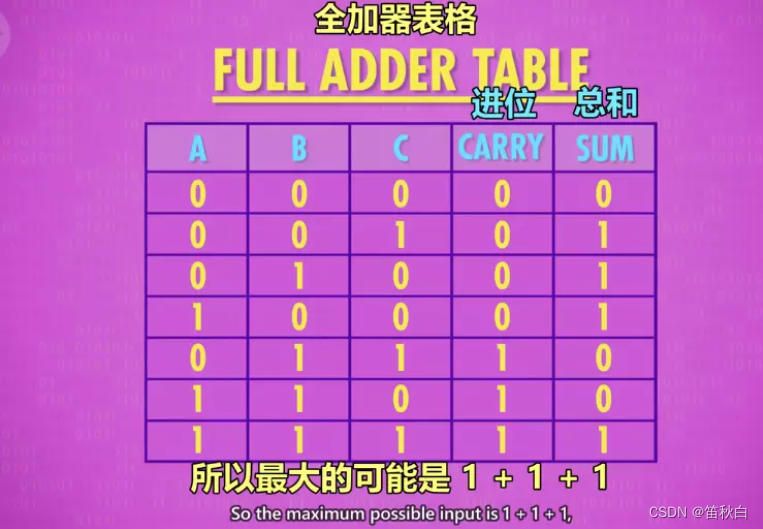 原理图示:
原理图示: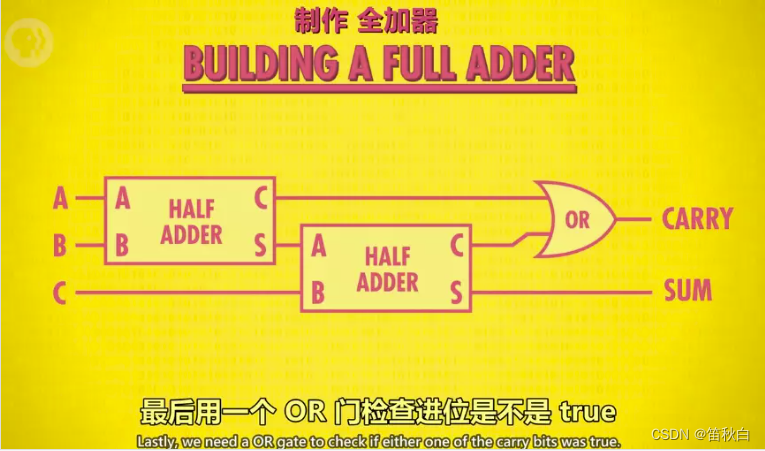
3)如何用半加器与全加器做 8 位数的加法
以 8 位行波加法器为例:
- 用半加器处理第 1 位数(个位)的加法,得到的和为结果的第 1 位。
- 将输出的进位,输入到第 2 位用的全加器的输入 C 中。
- 将第 2 位的 2 个数用全加器计算,得到的和为结果的第 2 位(sum)。
- 将第 2 位计算的进位连接到百位的全加器输入 C 中。
- 在第 3-8 位上,循环第 3-4 步的操作。
*现在电脑使用的加法器叫“超前进位加法器”。

4)算术单元支持的其他运算

3、溢出的概念
内容:在有限的空间内,无法存储位数过大的数,则称为溢出。
说明:第 8 位的进位如果为 1,则无法存储,此时容易引发错误,所以应该尽量避免溢出。
4、逻辑单元
作用:执行逻辑操作,如 NOT、AND、OR 等操作,以及做简单的数值测试。
5、ALU 的抽象
1)作用
ALU 的抽象让工程师不再考虑逻辑门层面的组成,简化工作。
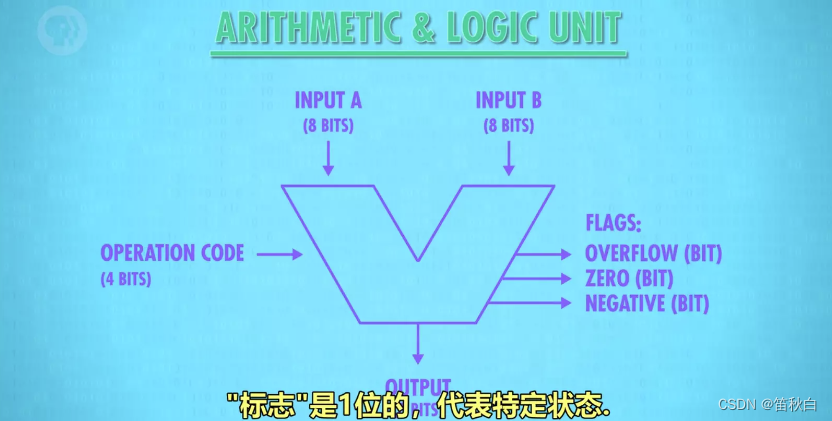
2)图示
像一个大“V”。

3)说明
图示内容包括:输入 A,B输出标志:溢出、零、负数
文章来源:https://blog.csdn.net/hellow_xqs/article/details/135229889
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!