DWA（dynamic window approach）算法学习

系列文章目录

A*算法学习-CSDN博客

弗洛伊德算法（Floyd）和路径平滑弗洛伊德算法（Smooth Floyd）学习-CSDN博客

D*算法学习-CSDN博客

---

目录

系列文章目录

前言

搜索空间?—减小速度搜索空间

优化过程?—最大化目标函数

算法实现

总结

---

前言

在机器人的路径规划中少不了DWA算法，学习！！！

DWA动态窗口法的原理及应用:The Dynamic Window Approach to Collision Avoidance - 知乎 (zhihu.com)

自动驾驶决策规划算法—DWA 动态窗口法 - 知乎 (zhihu.com)?

---

动态窗口法（Dynamic Window Approach， DWA）是一种避障规划方法，DWA算法通过对速度空间施加约束以确保动力学模型和避障的要求，在速度空间中搜索机器人最优控制速度，最终实现快速安全地到达目的地。

DWA算法的实现主要由两部分组成：?1.减小速度空间2.定义目标函数，并最大化目标函数

搜索空间?—减小速度搜索空间

通过施加弧线轨迹、允许速度、滑动窗口约束以减小搜索空间。

• 弧线轨迹 Circular trajectories
  在原论文中，作者对简化了机器人的运动学模型，并得出了机器人运动轨迹可由一系列弧线和直线组成。所以，作者将速度空间约束在由机器人的平移速度和旋转速度(v,w)组成的二维速度搜索空间。

• 允许速度 Admissible velocities
  允许速度（Admissible velocities）确保机器人可以在障碍前停下，最大的允许速度取决于当前轨迹距最近障碍的距离dist(v,w)。允许速度集被定义为：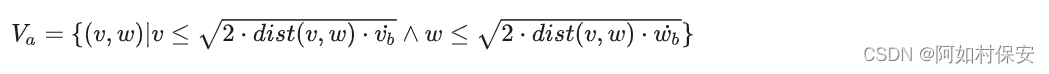

  

  下图中展示了Vs,Va速度空间：

  

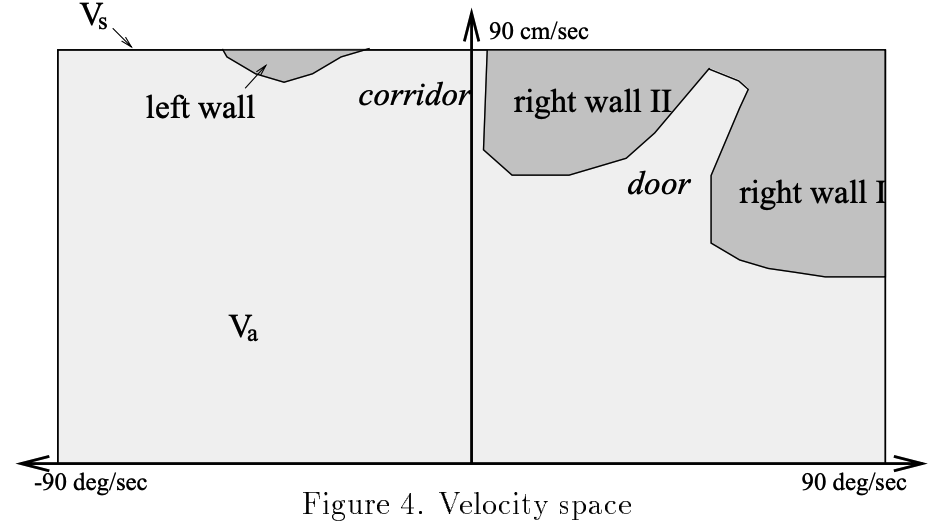
• 滑动窗口 Dynamic window
  考虑到机器人存在加速度限制，搜索空间被限定动态窗口Vd中（在下一个规划间隔可达到的速度），具体如下：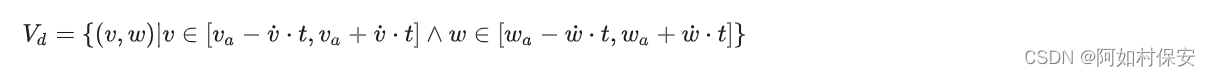

  

  其中，v˙,w˙表示机器人的加速度。
  最终的搜索空间：Vr=Vs∩Va∩Vd,如下图所示：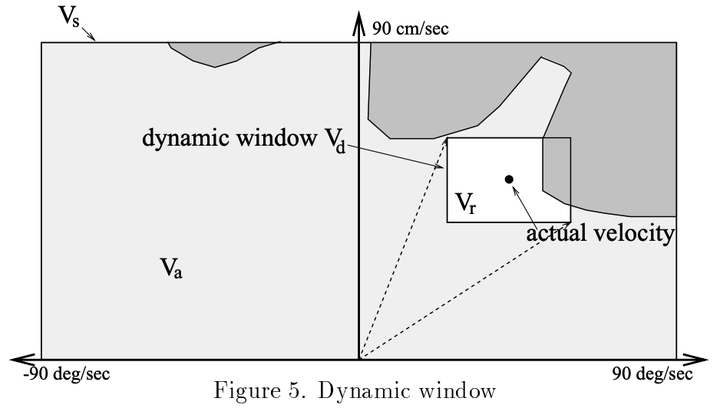

  

优化过程?—最大化目标函数

目标函数考虑了方位角、安全距离和速度：

• 方位角 Target heading
  方位角项heading(v,w)可确保机器人在运动过程中快速对准目标点。
• 安全距离 Clearance
  dist(v,w)确保机器人不发生任何碰撞
• 速度 Velocity
  速度项Velocity(v,w)可确保机器人尽快到达目标点

目标函数被定义为：

其中，?,??,???可以根据需求调整。这三个指标是目标函数的重要组成部分，缺一不可。仅使clearance和velocity最大化，机器人始终在无障碍空间运动，但不会有向目标位置移动的趋势。单独最大化heading，机器人很快就会被阻碍其前进的第一个障碍所阻挡，无法在其周围移动。通过组合三个指标，机器人在上述限制条件下能够快速地绕过碰撞，同时朝着目标方向运动。

算法实现

具体的DWA算法参考：https://github.com/AtsushiSakai/PythonRoboticsGifsplanning

函数讲解

• 动态窗口
  创建动态窗口

  def calc_dynamic_window(x, config):
    """
    calculation dynamic window based on current state x
    """
  
    # Dynamic window from robot specification
    Vs = [config.min_speed, config.max_speed,
          -config.max_yaw_rate, config.max_yaw_rate]
  
    # Dynamic window from motion model
    Vd = [x[3] - config.max_accel * config.dt,
          x[3] + config.max_accel * config.dt,
          x[4] - config.max_delta_yaw_rate * config.dt,
          x[4] + config.max_delta_yaw_rate * config.dt]
  
    #  [v_min, v_max, yaw_rate_min, yaw_rate_max]
    dw = [max(Vs[0], Vd[0]), min(Vs[1], Vd[1]),
          max(Vs[2], Vd[2]), min(Vs[3], Vd[3])]
  
    return dw
  

• 计算动态窗口内最优速度和最优轨迹

  • 在动态窗口dw中采样并计算可能的轨迹，并求解各条轨迹的目标函数
  • 选取令目标函数最小化（最小化指标，即对每个指标取倒数）的轨迹作为最优轨迹

  def calc_control_and_trajectory(x, dw, config, goal, ob):
    """
    calculation final input with dynamic window
    """
  
    x_init = x[:]
    min_cost = float("inf")
    best_u = [0.0, 0.0]
    best_trajectory = np.array([x])
  
    # evaluate all trajectory with sampled input in dynamic window
    for v in np.arange(dw[0], dw[1], config.v_resolution):
        # v_resolution: speed interval
        for y in np.arange(dw[2], dw[3], config.yaw_rate_resolution):
            # yaw_rate_resolution: yaw_rate interval
            trajectory = predict_trajectory(x_init, v, y, config)
            # calc cost
            to_goal_cost = config.to_goal_cost_gain * calc_to_goal_cost(trajectory, goal)
            speed_cost = config.speed_cost_gain * (config.max_speed - trajectory[-1, 3])
            ob_cost = config.obstacle_cost_gain * calc_obstacle_cost(trajectory, ob, config)
  
            final_cost = to_goal_cost + speed_cost + ob_cost
  
            # search minimum trajectory
            if min_cost >= final_cost:
                min_cost = final_cost
                best_u = [v, y]
                best_trajectory = trajectory
                if abs(best_u[0]) < config.robot_stuck_flag_cons \
                        and abs(x[3]) < config.robot_stuck_flag_cons:
                    # to ensure the robot do not get stuck in
                    # best v=0 m/s (in front of an obstacle) and
                    # best omega=0 rad/s (heading to the goal with
                    # angle difference of 0)
                    best_u[1] = -config.max_delta_yaw_rate
    return best_u, best_trajectory
  

• 目标函数

  • 方位角目标函数

  def calc_to_goal_cost(trajectory, goal):
    """
        calc to goal cost with angle difference
    """
  
    dx = goal[0] - trajectory[-1, 0]
    dy = goal[1] - trajectory[-1, 1]
    error_angle = math.atan2(dy, dx)
    cost_angle = error_angle - trajectory[-1, 2]
    cost = abs(math.atan2(math.sin(cost_angle), math.cos(cost_angle)))
  
    return cost
  

  • 障碍目标函数
    计算机器人与最近障碍的距离

  def calc_obstacle_cost(trajectory, ob, config):
    """
    calc obstacle cost inf: collision
    """
    ox = ob[:, 0]
    oy = ob[:, 1]
    dx = trajectory[:, 0] - ox[:, None]
    dy = trajectory[:, 1] - oy[:, None]
    # r = sqrt(dx^2 + dy^2)
    r = np.hypot(dx, dy)
  
    if config.robot_type == RobotType.rectangle:
        yaw = trajectory[:, 2]
        rot = np.array([[np.cos(yaw), -np.sin(yaw)], [np.sin(yaw), np.cos(yaw)]])
        rot = np.transpose(rot, [2, 0, 1])
        local_ob = ob[:, None] - trajectory[:, 0:2]
        local_ob = local_ob.reshape(-1, local_ob.shape[-1])
        local_ob = np.array([local_ob @ x for x in rot])
        local_ob = local_ob.reshape(-1, local_ob.shape[-1])
        upper_check = local_ob[:, 0] <= config.robot_length / 2
        right_check = local_ob[:, 1] <= config.robot_width / 2
        bottom_check = local_ob[:, 0] >= -config.robot_length / 2
        left_check = local_ob[:, 1] >= -config.robot_width / 2
        if (np.logical_and(np.logical_and(upper_check, right_check),
                           np.logical_and(bottom_check, left_check))).any():
            return float("Inf")
    elif config.robot_type == RobotType.circle:
        if np.array(r <= config.robot_radius).any():
            return float("Inf")
  
    min_r = np.min(r)
    return 1.0 / min_r  # OK
  

  最终机器人规划避障轨迹：

  

---

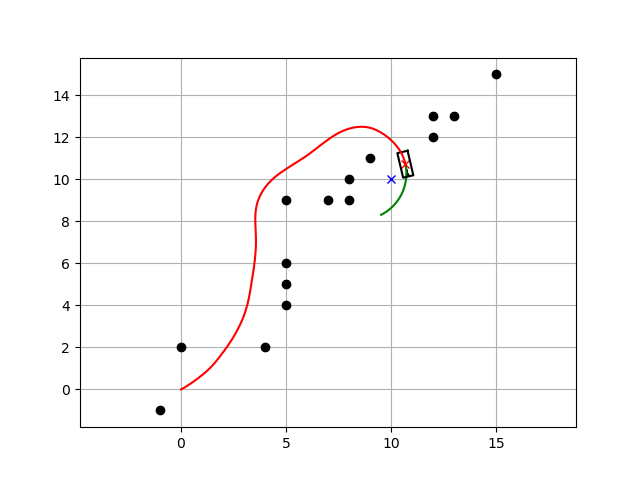
总结

机器人轨迹规划的基本算法，之后做实验跑一跑！！！之后还要研究下欧几里得距离转换算法(Euclidean Distance Transform, EDT)，建立EDT梯度图衡量障碍物代价以优化障碍物判断优化。