数据结构——堆
2023-12-25 16:55:13
1. 堆的概念
堆是一种特殊的树,满足如下条件:
-
完全二叉树:除了最后一层,其他层节点个数都是满的,最后一层的节点都集中在左侧连续位置。
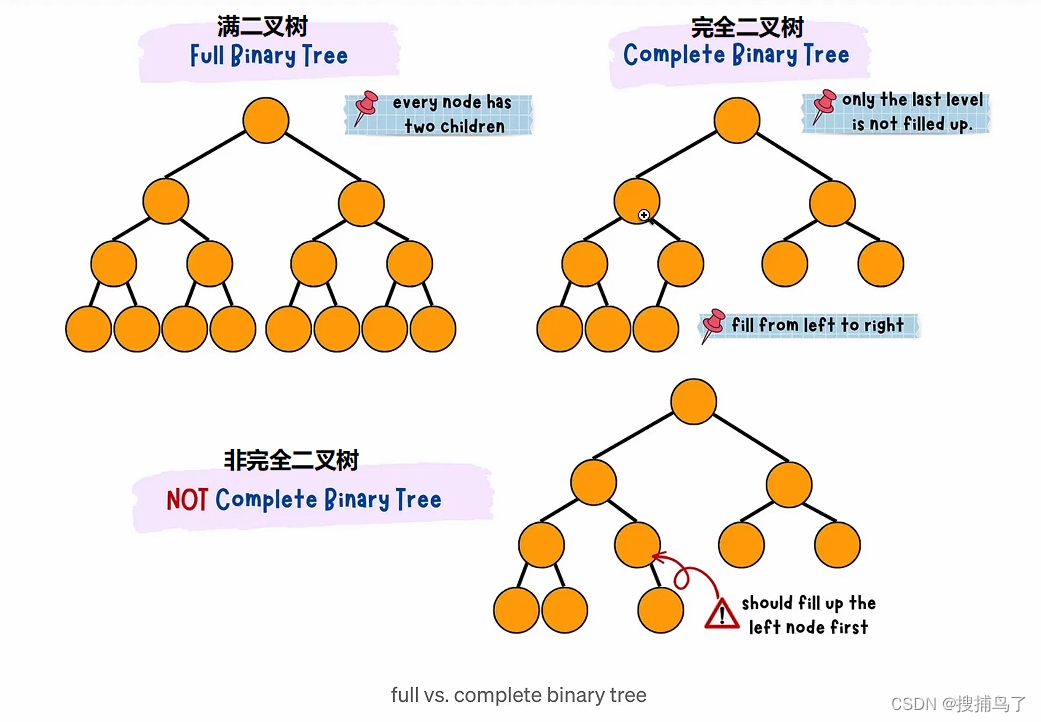
-
堆中每一个节点的值都必须大于等于(或小于等于)其左右节点的值。
- 每个节点都大于等于其左右节点的叫大根堆。
- 每个节点都小于等于其左右节点的叫小根堆。
堆和二叉搜索树的区别是:二叉搜索树的要求更为严格,它要求某个节点大于(小于)左侧节点小于(大于)右侧节点,而堆只要求某个节点大于(小于)左右两侧节点即可,因此同一组数据可以构建多种不同形态的堆。
2. 堆的表示
堆是完全二叉树,因此大部分时候使用数组来存储堆。
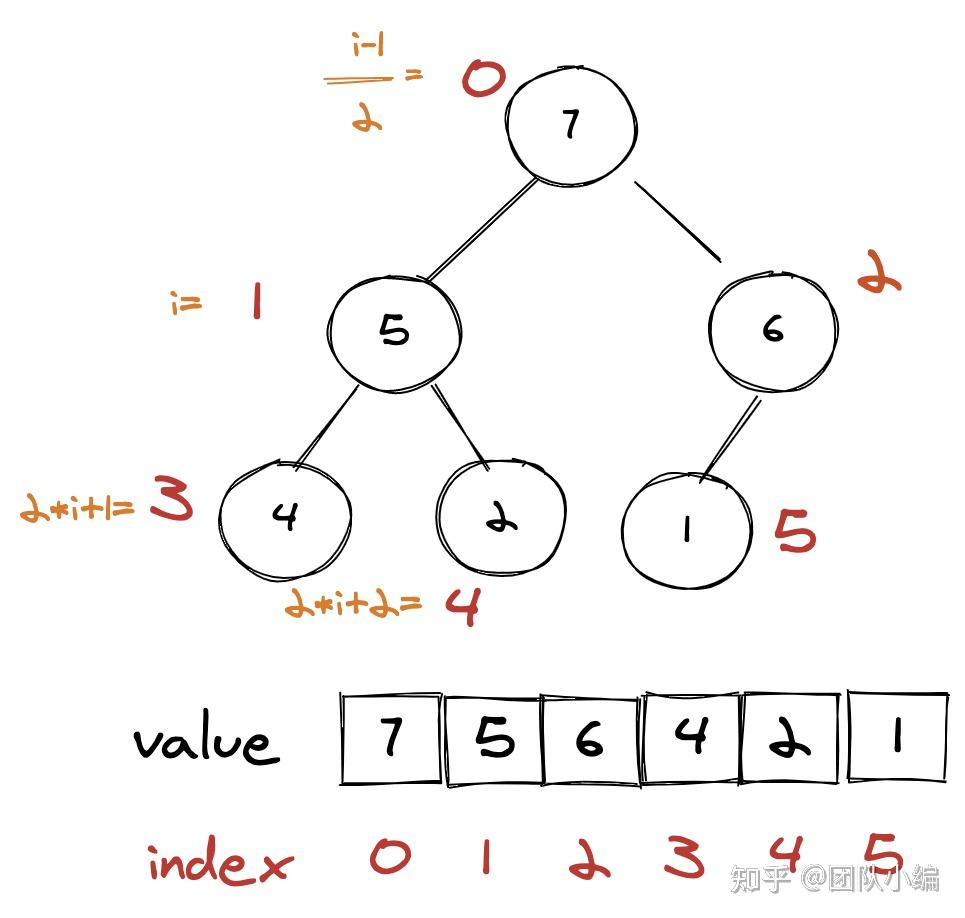
如上图,我们使用len来表示数组长度,i表示当前节点,我们可以总结出如下规律:
| 节点 | 索引 |
|---|---|
| 根节点root | 0 |
| 当前节点current | i |
| 父节点parent | floor((i - 1) / 2) |
| 左孩子节点left | i * 2 + 1 |
| 右孩子节点right | i * 2 + 2 |
| 最后一个孩子节点 |
3. 堆的构建
3.1 堆化
堆化指的是对数组元素顺序进行调整,以满足堆的特性,这个调整过程叫做堆化。
堆化分两种:
-
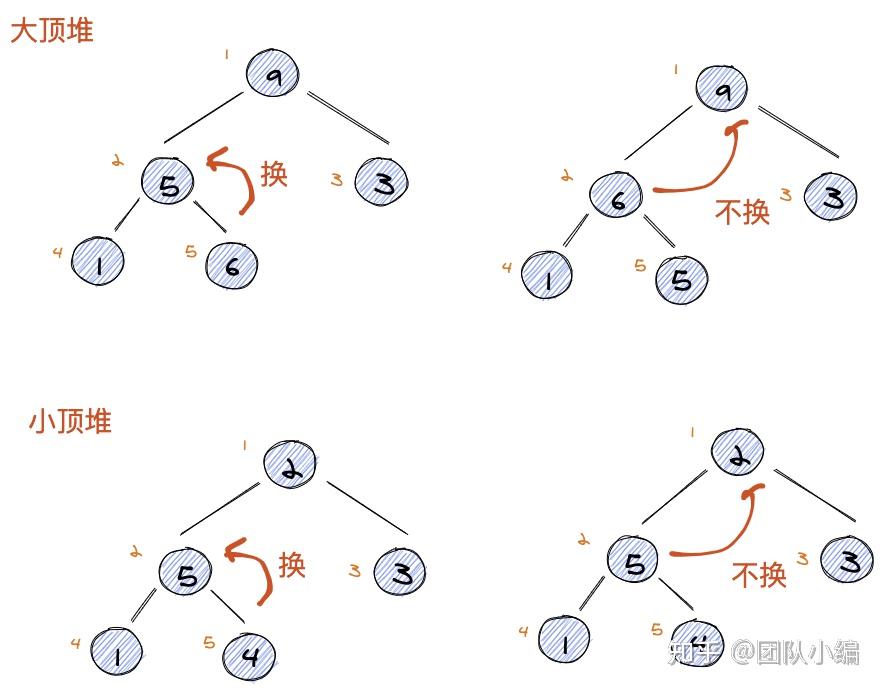
从下往上(上浮)
当前元素不断向上和父节点比较大小:
- 大顶堆:当前元素比父节点大,交换,让大的节点上去
- 小顶堆:当前元素比父节点小,交换,让小的节点上去
-
从上往下(下沉)
当前元素不断向下和两个孩子节点比较大小
- 大顶堆:当前元素与子节点中较大的比,比子节点小交换,让小的节点下去
- 小顶堆:当前元素与子节点中较小的比,比子节点大交换,让大的节点下去

3.2 构建堆的思路
通过上小节我们了解到,堆化是对有孩子节点的节点进行的操作,因此我们只需要对二叉树的每个非孩子节点进行堆化即可得到堆。根据2.堆的表示那节总结的规律可知最后一个非叶子节点的索引为Math.floor(len / 2) - 1,因此我们对需要对数组从此索引开始向0遍历,依次对节点进行堆化即可得到一个堆。
4. 堆的代码实现
这里以大根堆为例,下面我们通过代码实现一个简单的大根堆类,其中包括堆的初始化,插入元素,删除堆顶元素这三个功能。
class Heap {
constructor(arr) {
this.arr = arr;
this.heapify();
}
/**
* 堆化
*/
heapify() {
for (let i = Math.floor(this.arr.length / 2) - 1; i >= 0; i--) {
this.sink(this.arr, i);
}
}
/**
*
* @param {Array} arr
* @param {Number} i
* arr[i]节点的下沉操作,即自顶向下堆化
*/
sink(arr, i) {
// 当左孩子节点的索引合规
while (2 * i + 1 < arr.length) {
let j = 2 * i + 1; // 初始化将最大孩子节点指针指向左孩子
if (j + 1 < arr.length && arr[j + 1] > arr[j]) {
// 如果当前节点的右孩子比左孩子更大 最大孩子节点指针指向右孩子
j++;
}
if (arr[i] > arr[j]) {
// 当前节点的左右儿子都 <= 当前节点,停止下沉
break;
}
// 下沉——交换值
[arr[i], arr[j]] = [arr[j], arr[i]];
// 下沉——更新当前操作的节点i
i = j;
}
}
/**
*
* @param {Number} val
* 向堆中插入值为val的元素,val插入数组最后一位,自底向上堆化
*/
insert(val) {
this.arr.push(val);
let i = this.arr.length - 1; // 初始化当前操作的节点 即插入节点的索引
while (i > 0) {
let j = Math.floor((i - 1) / 2); // 父节点的索引
if (this.arr[i] <= this.arr[j]) {
// 当前节点小于等于父节点 停止上浮
break;
}
// 上浮——交换
[this.arr[i], this.arr[j]] = [this.arr[j], this.arr[i]];
// 上浮——更新当前操作的节点i
i = j;
}
}
/**
*
* 删除堆顶元素
*/
delete() {
let len = this.arr.length;
// 将最后一个元素值和堆顶互换
[this.arr[len - 1], this.arr[0]] = [this.arr[0], this.arr[len - 1]];
// 删除最后一个元素
this.arr.pop();
// 下沉
this.sink(this.arr, 0);
}
}
验证结果:
let heap = new Heap([1, 6, 5, 6, 88, 3, 5, 10]);
console.log(heap.arr); // [88, 10, 5, 6, 6, 3, 5, 1]
heap.insert(100);
console.log(heap.arr); // [100, 88, 5, 10, 6, 3, 5, 1, 6]
heap.delete();
heap.delete();
heap.delete();
heap.delete();
console.log(heap.arr); // [ 6, 5, 5, 1, 3 ]
根据结果可以看到完全符合大根堆的要求。
参考:
文章来源:https://blog.csdn.net/weixin_43599321/article/details/135202056
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!