PolarNet: 一种改进的时实激光雷达点云语义分割网格表示方法
PolarNet介绍
github工程代码:https://github.com/edwardzhou130/PolarSeg
点云语义分割在自动驾驶领域的感知模块占据重要地位, 从多年前基于传统的点云聚类和分割,到近些年基于深度学习的点云语义分割方法, 技术逐渐成熟已经进入实时端到端的阶段. 前有基于球面投影映射出二维深度图的SqueezeSeg,后又百度的Apollo和Autoware中开源的基于鸟瞰图二维网格的cnn_seg. 本文将介绍一种较新的点云语义分割方法: PolarNet,以及它的升级版点云全景语义分割方法:Panoptic-PolarNet.
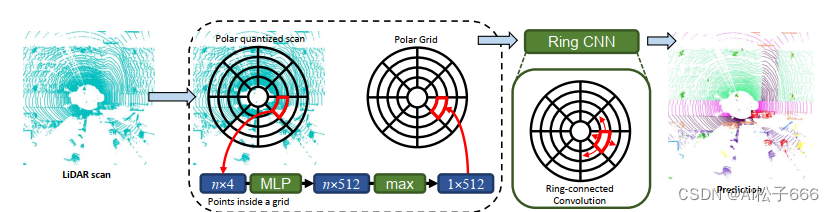
从整体结构来看,PolarNet和多数点云语义分割网络结构一样, 针对点云数据的特点: 空间分布稀疏性,无序性和随是三维数据却无法直接应用三维卷积(计算量剧增)等问题, 先将三维点云的鸟瞰图映射为二维图像,然后使用编码器-解码器结构的全卷积网络进行逐像素的分类. 这里PolarNet使用U-Net网络的编码阶段来学习不同尺度的特征,使用解码器阶段完成每个像素点的分类.
关于U-Net网络及其升级版U-Net++,U-Net3+, 其主体网络都是基于FCN网络, 只是在垮层级间的深浅特征融合方式上做了不同的调整. 使网络可以提取和学习到更为细节的图像信息,语义分割效果也更佳.
所以, PolarNet主要思想重点就放在如何将3维点云的鸟瞰图映射为二维图像上. 同样的思想, SqueezeSeg的实现方法是通过将3维点云经球面投射映射为一个二维的深度图,cnn_seg的实现方法是将3维点云鸟瞰视图向地面投影映射为直角坐标系网格的二维网格.
PolarNet的基于极坐标的鸟瞰图(Bird Eye View, BEV)投影:
PolarNet对BEV投射的采用了极坐标系来分割二维投影映射(这让我想起了有一种基于传统方法的点云地面分割算法,也采用了类似的方法,在<<二十五. 智能驾驶之基于点云分割和聚类的障碍物检测>>做了介绍). 这有别于其他算法对BEV投影以笛卡尔坐标系来分割二维投影映射(二维网格).如下图所示:
(以笛卡尔坐标系分割二维鸟瞰图)
(以极坐标系分割二维鸟瞰图)
如上图,PolarNet采用了极坐标系替代笛卡尔坐标系,使用极角θ和极径ρ表示的有序对(ρ,θ)来代表点云的投影分区,按照极坐标系网格对平面进行划分,这种做法能够进一步使得点在网格间均匀分布,远距离的网格也能保留更多的点。特别是对地面,可以保证同一条激光扫描线落在同一个分区内.
基于极坐标系分割鸟瞰图BEV的过程(图片来源原伦文供图):
PolarNet训练了一个简单的PointNet(注:此PointNet不是语义分割网络PointNet)神经网络用于极坐标网格内的特征提取. 如上图, 对点云的处理大致分以下几步:
一. 将一帧点云从鸟瞰图BEV视角投射到地面,映射为一个二维平面映射图. 并以车身载体坐标系原点为中心点,建立极坐标系.
二. 在极坐标系中,按照预设的角度偏移θ为step,将0-360度的极坐标系平分为360/θ=N份扇面,类似于磁盘单个盘面的扇区感念, 同时在以原点为中心的径向方向,按照预设的半径偏移ρ,向外等分出一系列同心圆, 类似于磁盘单个盘面的柱面. 此时,由不同的扇区和同心圆,就将整个有效极坐标系内的点云,分成若干个不同的扇形网格, 类似于磁盘单盘面的一个扇区.
三. 使用代码内置的一个PointNet对每一个扇形网格进行学习得到一个固定长度的特征表示.
四. 因为每一个同心圆环是有若干个扇形网格环绕一周连接而成,即它们是首尾连接的. 为了学习到的特征完整不间断,把学习到的每一个同心圆环内的扇形网格的特征也按原顺序首尾拼接,形成一个环形特征表示.
五. 将学习到的环形特征表示输入一个Ring CNN的神经网络中学习其整体特征.
Ring CNN就是基于环卷积的卷积神经网络,这也是PolarNet的独到之处. 普通的卷积网络输入的特征是个平面二维数据. Ring CNN这里输入的是将平面首尾连接的特征, 使用卷积核循环一边卷积操作,以保证不遗漏极坐标系下同心环的连接处的特征(详细参见其官方源码).
极坐标划分
点云有越远越稀疏的特性,相对于传统的BEV视角,点云分割更加的均匀。
1、极化鸟瞰图
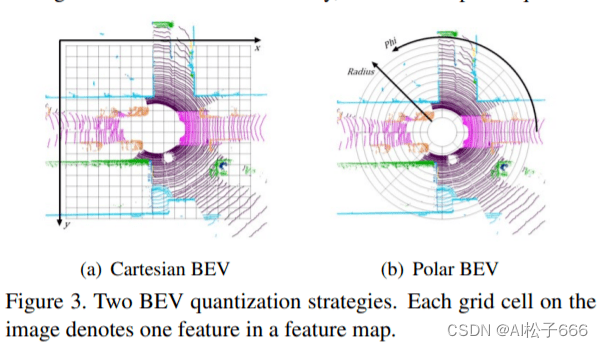
基于LiDAR扫描俯视图出现的环形结构,作者展示了图3所示的Polar分区,取代了图3中的笛卡尔分区。具体地,首先以传感器的位置为原点,计算XY平面上每个点的方位角和半径,而不是对笛卡尔坐标系中的点进行量化。然后将点云分配给根据量化方位角和半径确定的网格单元。
极化BEV有两个好处,首先,它可以更平均地分配点。通过统计SemanticKITTI数据集拆分的验证集,发现每个极点栅格像元靠近传感器时的点数远小于笛卡尔BEV中的点数。因而,用于密集区域的网格的表示更精细。在相同数量的网格单元中,传统的BEV网格单元平均为0.7±3.2点,而极性BEV网格单元平均为0.7±1.4点。标准偏差之间的差异表明,总体而言,这些点在极地BEV网格上分布更均匀。
极化BEV的第二个好处是,更平衡的点分布减轻了预测变量的负担。由于将2D网络输出重塑为体素以进行点预测,因此不可避免地,某些具有不同真实值标签的点将分配给同一体素。而且其中有些无论如何都会被错误分类。使用笛卡尔BEV,每个网格单元中平均98.75%的点共享相同的标签。在极化BEV中,这一数字跃升至99.3%。这表明由于空间表示特性,极化BEV中的点较少遭受错误分类。考虑到小物体更有可能被体素中的多数标签所淹没,这种0.6%的差异可能会对最终的mIoU产生更深远的影响。研究mIoU的上限表明,笛卡尔BEV的mIoU达到97.3%。极化BEV达到98.5%。极化BEV的较高上限可能会提高下游模型的性能。

2、环形卷积
无需随意为每个网格手工绘制特征,而是使用固定长度的表示形式捕获每个网格中的点分布。它是由可学习的简化PointNet [22] h和最大池化产生的。该网络仅包含完全连接的层,批处理规范化和ReLu层。扫描中第i,第j网格单元中的特征为:
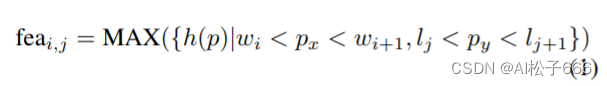
其中w和l是量化大小。px和py是地图中点p的位置。注意,位置和量化大小可以是极坐标或笛卡尔坐标。我们不对沿z轴的输入点云进行量化。类似于point pillar,学习到的表示表示网格的整个垂直列。
如果表示是在极坐标系中学习的,则特征矩阵的两侧将在物理空间中沿方位轴连接,如图2所示。作者开发了离散卷积,称为环形卷积。假设矩阵在半径轴的两端相连,则环形卷积核将对矩阵进行卷积。同时,位于相反一侧的梯度可以通过该环形卷积核传播回另一侧。通过在2D网络中将常规卷积替换为环形卷积,该网络将能够端到端处理极坐标网格,而不会忽略其连通性。这为模型提供了扩展的应用范围。由于它是一个2D神经网络,因此最终的预测也将是一个极坐标网格,其特征维等于量化的高度通道和类数的乘积。然后,可以将预测重塑为4D矩阵,以得出基于体素的分割损失。将卷积替换为环形卷积,则大多数CNN在技术上都可以处理极坐标网格。作者将具有环形卷积的网络称为经过训练以处理极化网格的环CNN。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!