认识机器学习【woodwhales.cn】

为了更好的阅读体验，建议移步至笔者的博客阅读：认识机器学习

生活中的问题1：居民家庭生活用气价格

北京燃气小程序在线咨询，查询北京居民家庭生活用气价格

上图价格梯度，可以由文字转换成表格：

第一档用气量为0-350（含）立方米，气价为2.61元/m3；

第二档用气量在350-500（含）立方米之间，气价为每立方米2.83元/m3；

第三档用气量为500立方米以上，气价为每立方米4.23元/m3。

分档	用气量（立方米）	价格（元/立方米）
第一档	0-350（含）	2.61
第二档	350-500（含）	2.83
第三档	500以上	4.23

某居民使用一些天然气之后，需要知道应该支付多少费用，该使用什么函数来计算：居民家庭生活用气量 x 与 价格 f(x) 的关系：

利用初中数学知识，可以得到居民家庭生活用气量 x 与 价格 f(x) 的函数关系为：

生活中的问题2：北京市部分区域二手房房价

以 2023年11月30日北京市部分区域二手房房价为例

如何从上图的二手房真实价格中，找出面积和房价的函数关系？

二手房价的数学函数表达

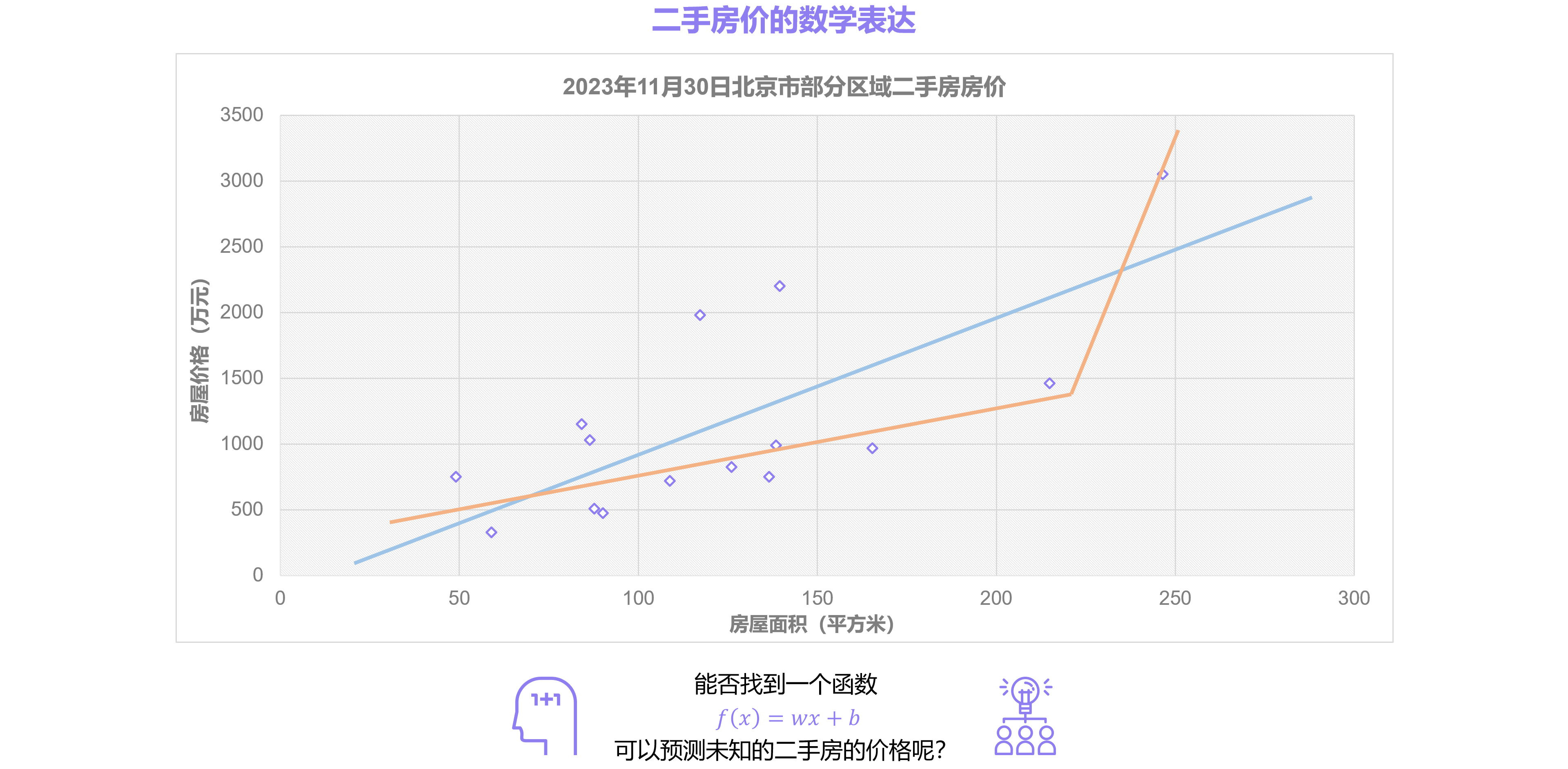
将上章节中的面积和房价形成一个个二位坐标点信息，放到二位坐标系中，能否找到一条直线或者曲线来表达：面积和房价的关系：

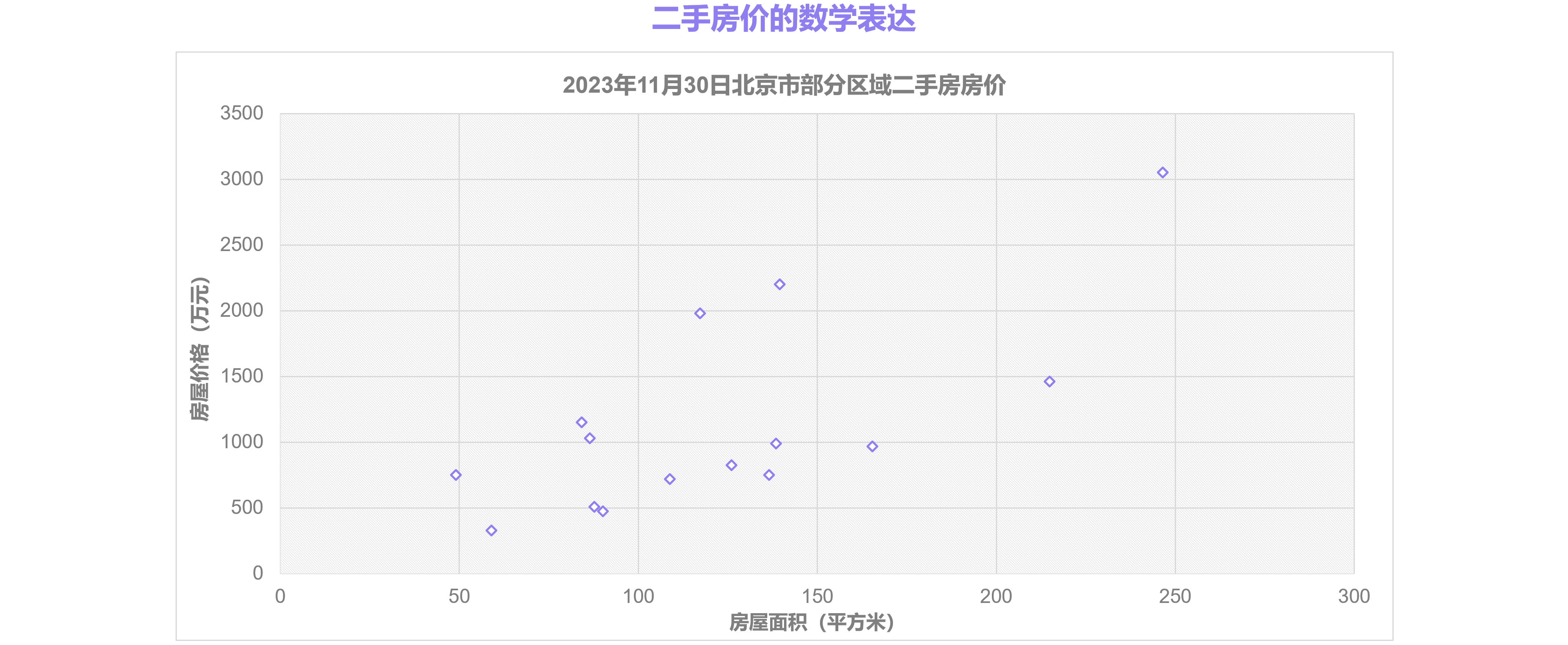
从直觉来看，可以绘制如下可能的函数直线或曲线：

从上图中可以看到：蓝色和橙色函数均可以表达面积和房价的关系，但是哪一条是最合适的需要有充分的说服力。

我们知道，房价的影响因素很多，还有诸多因素：

每一个影响因素可以使用形如面积和房价的函数关系式表达，所有因素之和最终决定了房价：

从上述房价的函数式可以知道，房价最终是由 w 和 b 决定。

结合线性代数的矩阵转置基础知识，可以将上述函数式简化表达：

假设我们已经找到参数对（W1, b1）是房价函数的可能最优解，那么如何来确认这个参数对就一定是最优解呢？

正如上图所说：如果存在某个函数存在，使得能精准预测所有真实结果，则该函数为最优解。但是现实情况中，可能没有最完美的函数。那如何在所有“差的”函数中找到“最不差的”？

利用高中的期望知识可以得到：真实值 – 预测值 = 差值（代价），所有差值之和最小则为最优解。即：只要存在参数对（W1, b1）利用房价函数的得到的所有房价和其真实房价差距最小则为最优解。

代价函数

从上述可以得到下述三个函数式

将上图中的下方俩个函数带入第一个函数，可以简化成如下：

对于函数 g(w,b) 的参数对 (w,b) 数值进行穷举，会得到诸多 g 和 g（w, b）的数据对，将这些数据对绘制到三维坐标系中，可以表示为如下图：

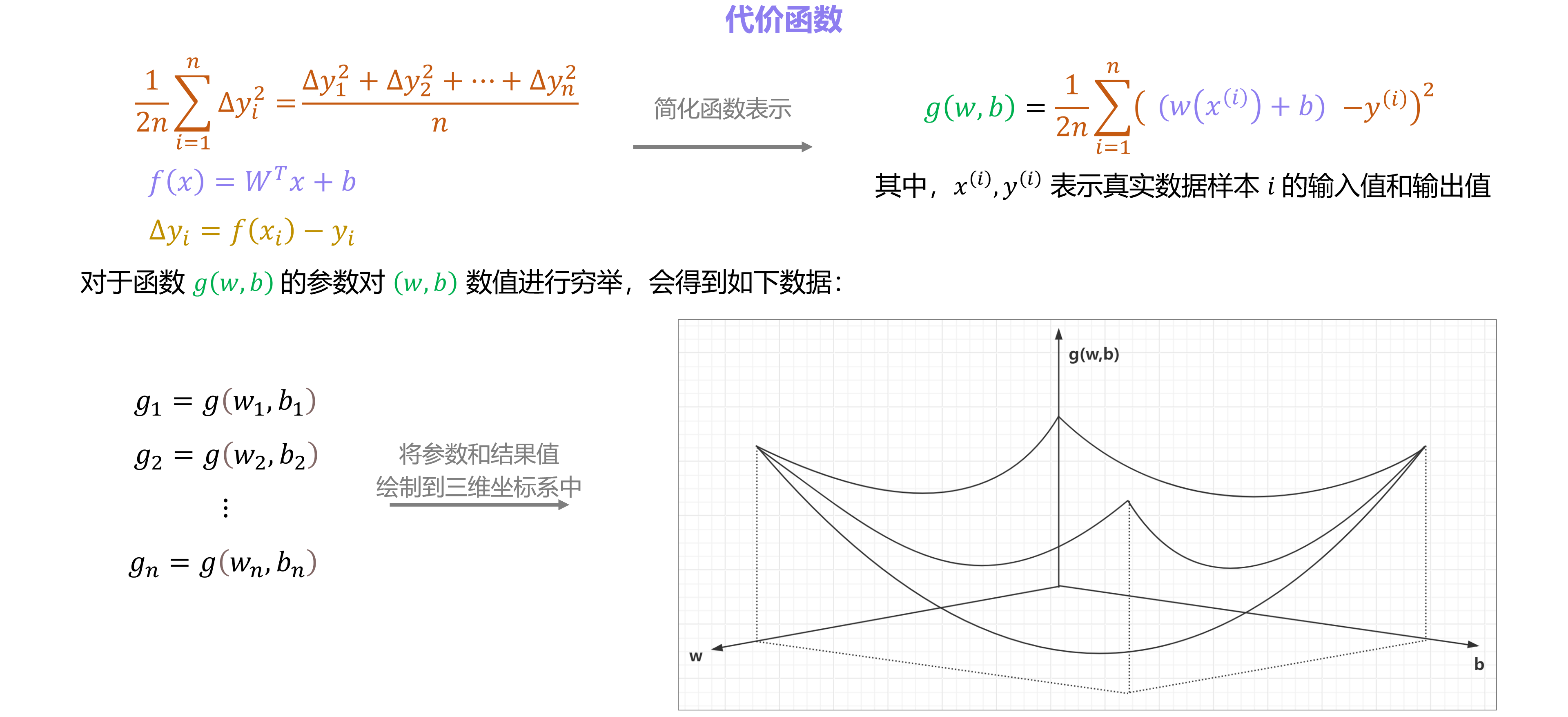
梯度下降

从上图可以看到，三维坐标系中的函数图像”最低处“就是方差最小的地方，也就是参数对（w, b）对于房价函数的最优解。求“最低点”的方法叫：梯度下降算法。

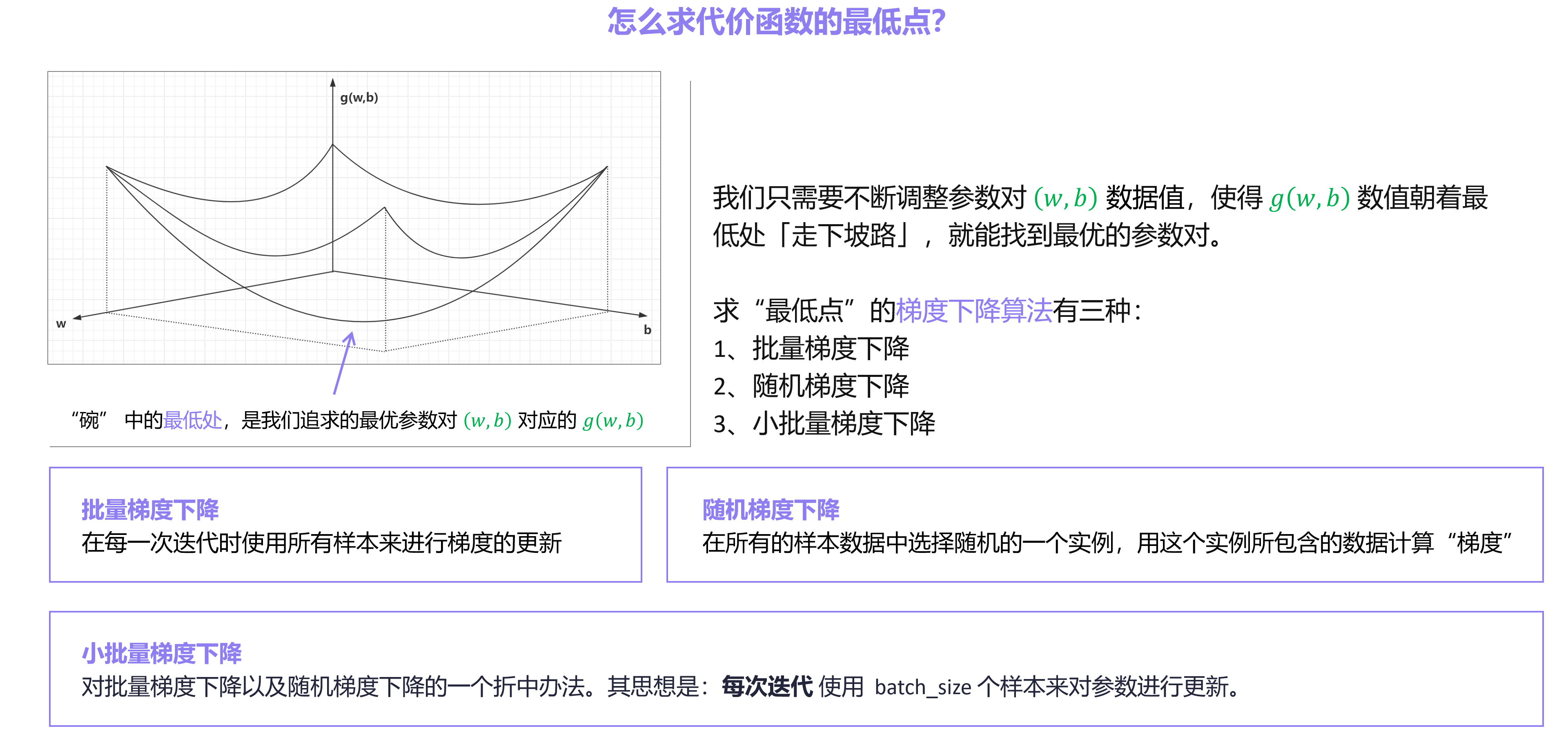
通过上述推理，可以得知，想要找到房价函数的最优解，就是在找代价函数的最优解。

类推其他问题

生活中除了房价问题，还有很多类似问题都是需要人类找到最优的函数：

上图中函数就是在解答相应的问题，那么谁来解决帮我们找到最优函数呢？答案不言而喻。

常见的机器学习问题

常见的机器学习问题可以归类为：回归问题、分类问题、聚类问题

机器学习算法的分类

按学习的方式来划分：

• 监督学习
• 非监督学习
• 半监督学习
• 强化学习

按功能来划分：

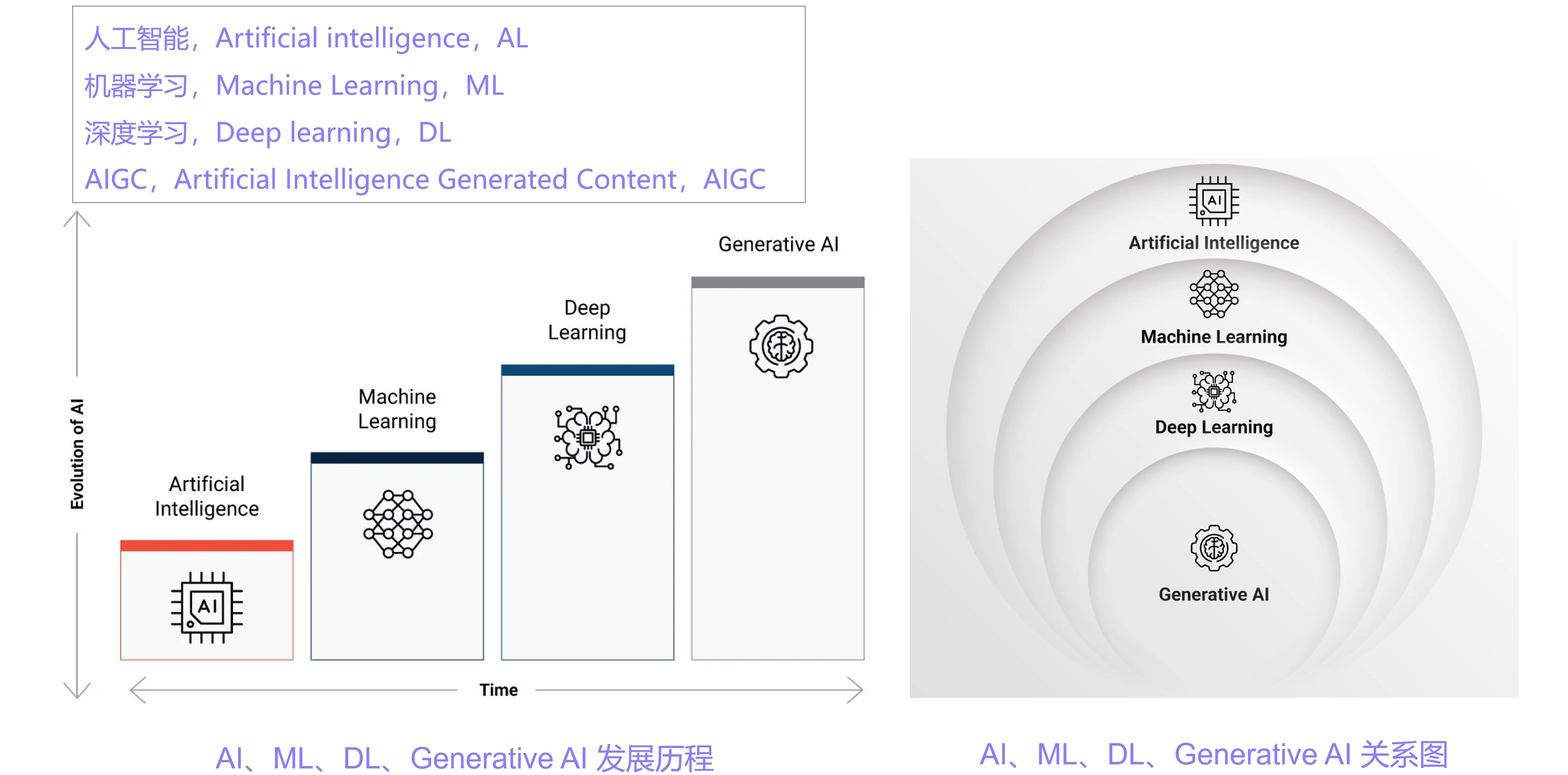
AI、ML、DL、 AIGC

AI、ML、DL、 AIGC 四者的关系如图：

参考资料

文字资料

神经网络与深度学习-邱锡鹏

https://medium.com/@ageitgey/machine-learning-is-fun-80ea3ec3c471#.ak1of1xbg

https://synoptek.com/insights/it-blogs/data-insights/ai-ml-dl-and-generative-ai-face-off-a-comparative-analysis/

https://feisky.xyz/machine-learning/basic.html

https://cloud.google.com/learn/what-is-artificial-intelligence?hl=zh-cn

视频资料

下述视频资料可以在 B 站上找到同名视频

机器能像人一样思考吗？人工智能（一）机器学习和神经网络

人脸识别啥原理？人工智能（二）卷积神经网络

“神经网络”是什么？如何直观理解它的能力极限？它是如何无限逼近真理的？