【计算机图形学】《五讲速通CG重点》第二讲-Viewing

?如果这篇文章对你有帮助，欢迎点赞与收藏~

目录

2D_3D_transformation

?编辑

1 Homogeneous coordinate 齐次坐标

2 Affine transformation 仿射变换

3 Composite transformations

4 3D transformations

2D_3D_viewing

1 The process of viewing

2 Projection transformation

2.1 Orthogonal projection

2.2 Perspective projection ？

3 Clipping

3.1 Why？

3.2 Cohen-Sutherland Algorithm

3.3 Weiler-Atherton Clipping

3.4 Sutherland-Hodgman Polygon Clipping

Visible surface detection

1 Back face culling

2 Painter’s Algorithm

3 BSP Tree (Binary space partitioning)

4 Z-buffer complexity (n*m*k)

2D_3D_transformation

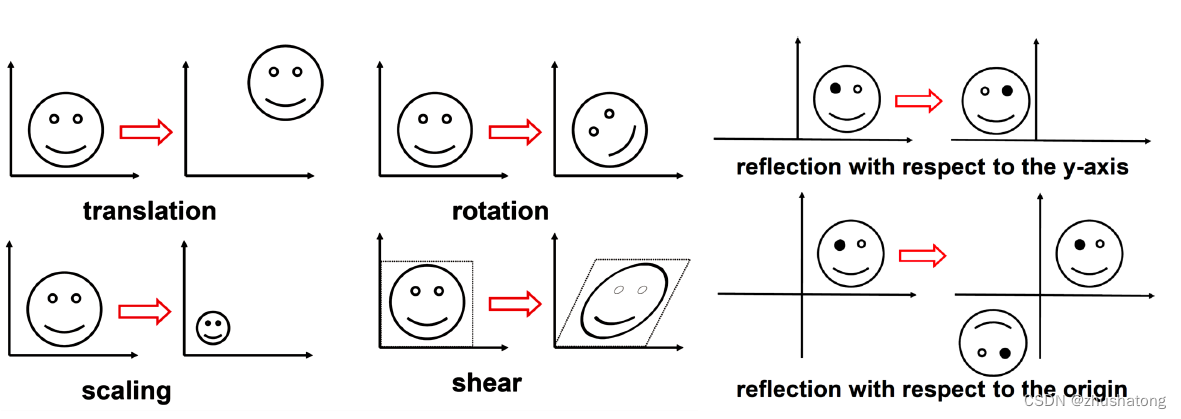
线性：Rotation, scale, shear, reflection are all linear but translation is not linear.

可交换：Only the same kinds of transformation are commutative.

1 Homogeneous coordinate 齐次坐标

Point refers that the last coordinate is 1

Vector refers that the last coordinate is 0

--> point - point = vector

2 Affine transformation 仿射变换

translation together with linear transformations

Translation: Move dx, dy

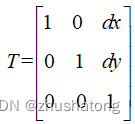
Rotation(counterclockwise)

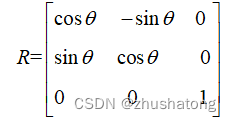
Scale

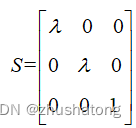
Rigid-motion: translation+rotation

3 Composite transformations

Rotate about a particular point : translate to the origin | rotate | translate back

Transformation of local coordinate systems---> obtain the coordinate in world space （以原先local coordinate原点为原点的世界系）

𝑝𝑛 is the world coordinate of point p after n transformations

4 3D transformations

Translation

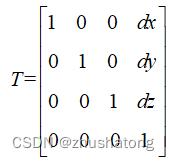
Scale

空间中的三维旋转（欧拉角的矩阵）四元数

2D_3D_viewing

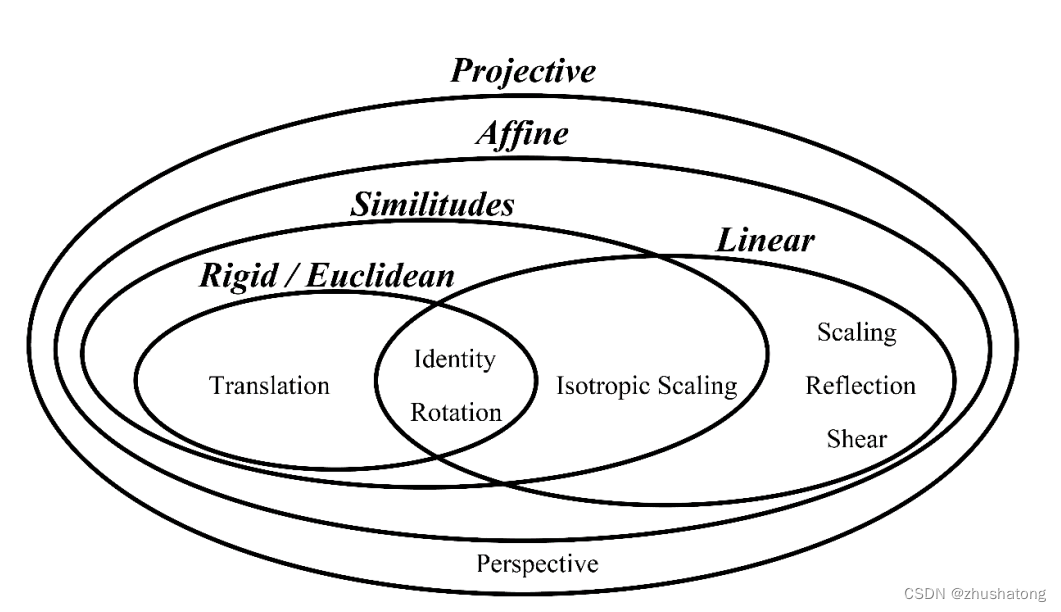
内侧的椭圆是“Affine”（仿射），仿射变换是射影变换的一个子集，它保持了图形的平行性。仿射变换包括了“Similaritudes”（相似）和“Linear”（线性）变换。

“Similaritudes”椭圆进一步细分为“Rigid / Euclidean”（刚体或欧几里得）变换，这种变换包含了平移（Translation）、旋转（Rotation）和恒等（Identity）。这些变换保持了图形的形状和大小不变。

在“Linear”变换的范围内，有“Scaling”（缩放），“Reflection”（反射），“Shear”（剪切），以及“Isotropic Scaling”（等距缩放）。这些变换可以改变图形的大小，但可能会改变其形状。

“Perspective”（透视）在图的底部被提及，它通常关联于射影变换，但在这个图中没有被包含在任何椭圆内，这可能意味着它作为一个独立概念存在，涉及从特定视点观察物体时的变换。

The camera is located at origin and point in the -z direction.

1 The process of viewing

Transform into camera coordinate

-> perform projection into view volume (orthogonal transformation/perspective transformation)

-> clip geometry outside the clipping volume

-> project into screen coordinate(perspective division & viewport NDC)

-> remove hidden surface

Model view matrix:

If we want to visualize objects with both positive and negative z values, we can move the camera in the positive z direction/ move the objects in the negative z direction.

2 Projection transformation

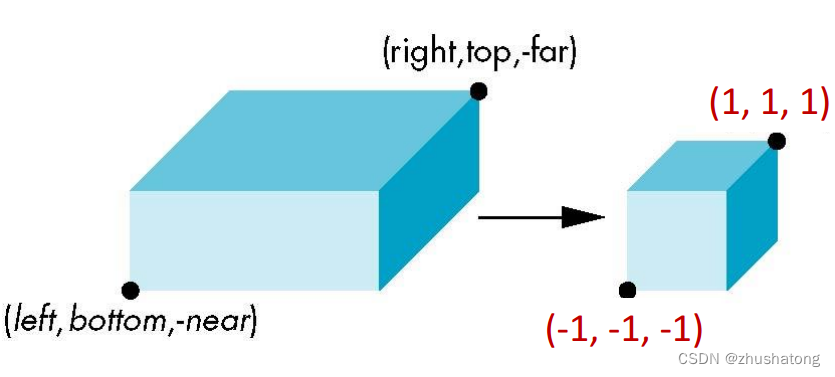
2.1 Orthogonal projection

1. Translation center to origin

T( -(left+right)/2 , -(bottom+top)/2 , (near+far)/2 )

1. Scale to have sides of length 2

S ( 2/(right-left) , 2/(top-bottom) , 2/(-far-(-near)) )

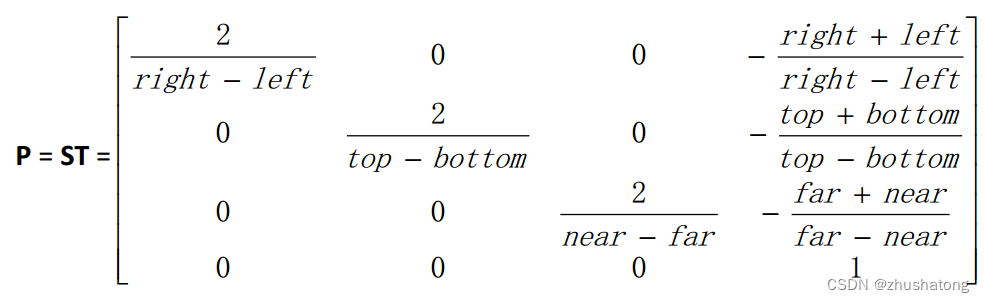Pay attention to left, right, bottom, top, -near, -far (the positive direction of z is outside the screen)

Final projection

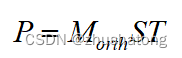
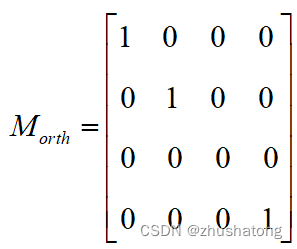
2.2 Perspective projection

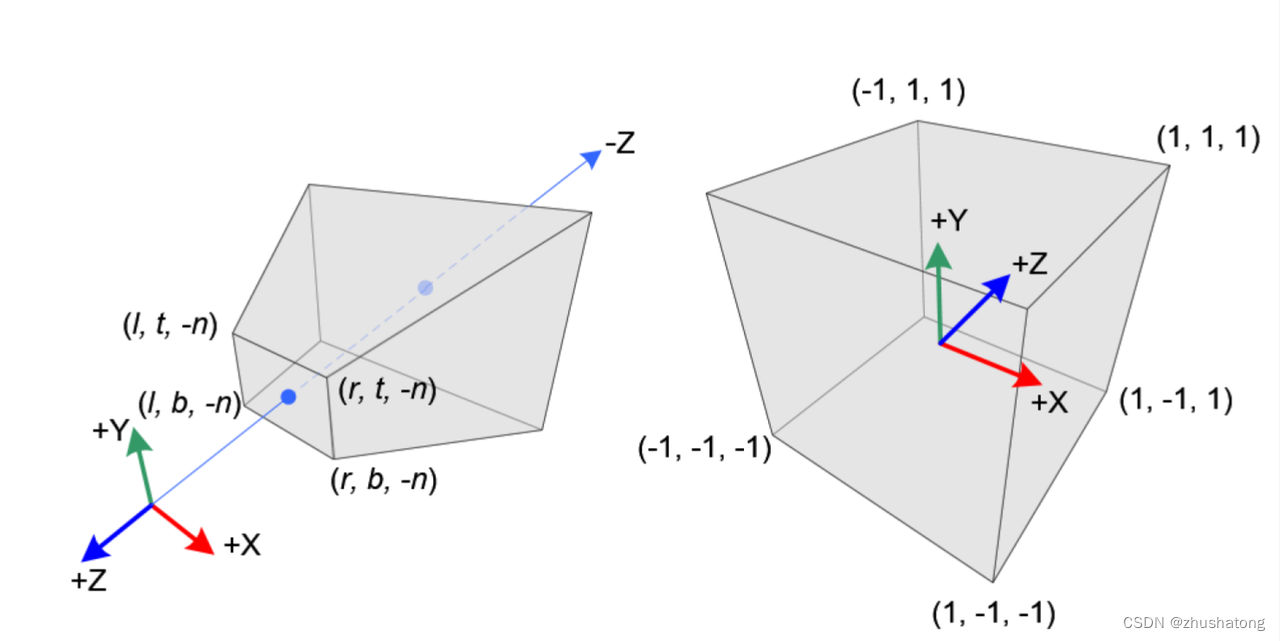
Given the (xe,ye,ze) is coordinate in eye space. The coordinate of projection :

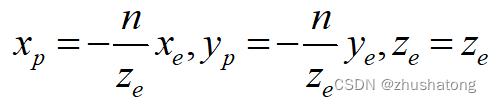
Then do the operation like orthogonal projection:

Translate and scale: n means normalize / c means clipping

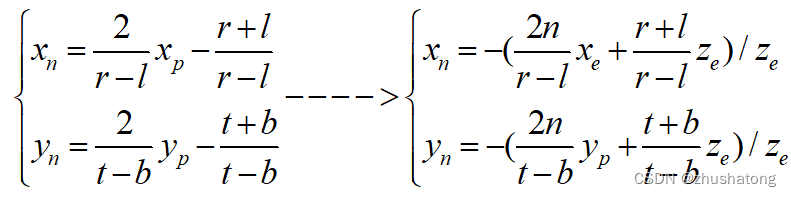
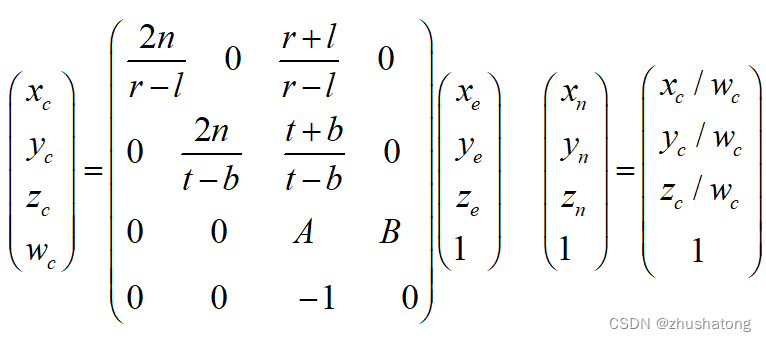
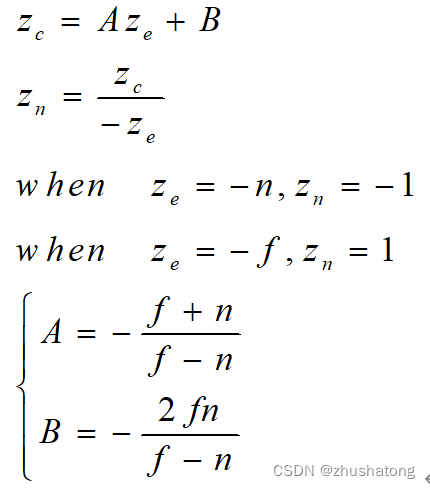
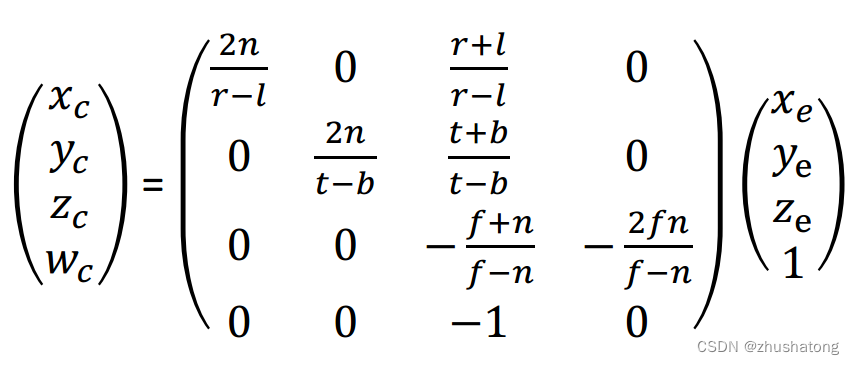
3 Clipping

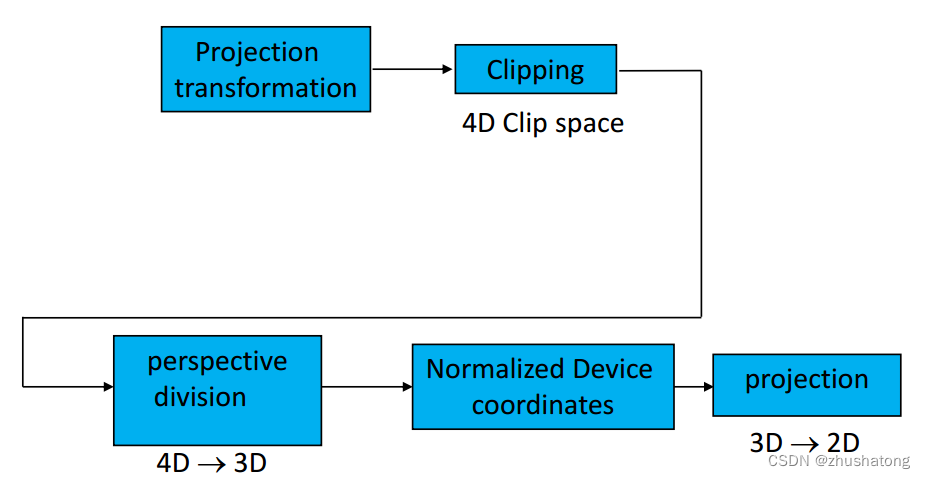
Perspective division could cause what should be clipped in clipping volume projected into NDC?

3.1 Why？

Avoid division by 0 && don’t draw things behind the eye

Don’t waste time on objects outside the boundary.

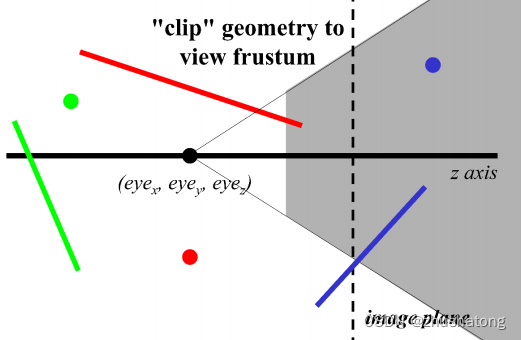
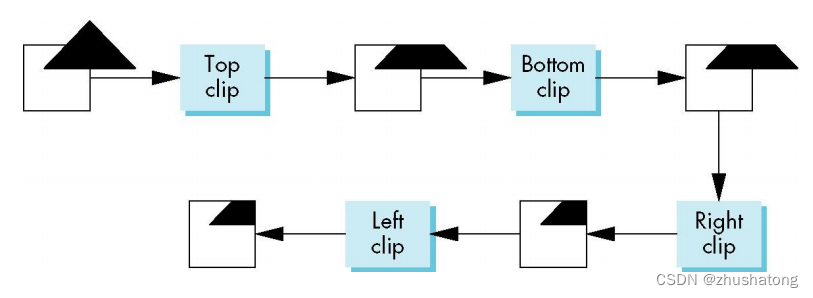
3.2 Cohen-Sutherland Algorithm

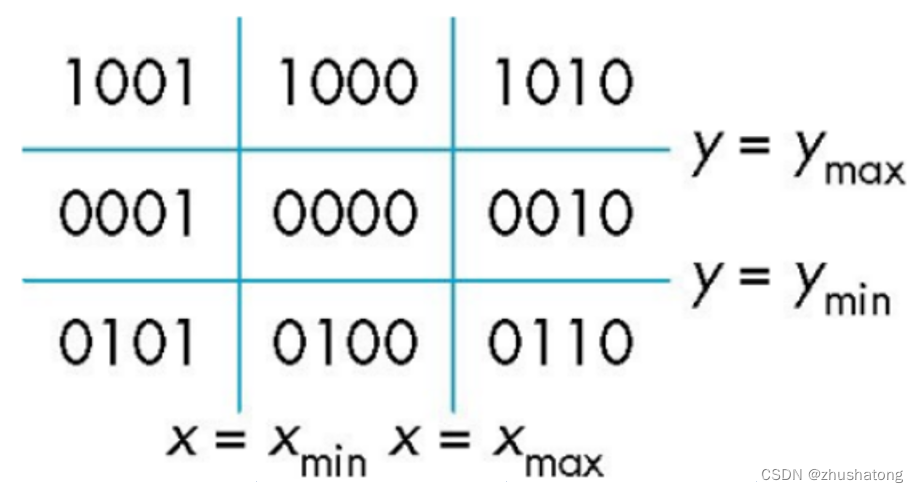
The bit means up, down, right, left from left to right respectively.

If the code of two endpoints is all 0000, it means the segment is in clipping window.

If the result of intersecting the code of two endpoint concludes 1, it means the segment is out of clipping window.

3.3 Weiler-Atherton Clipping

多边形序列

裁剪窗口序列 逆时针进行排序

当在多边形序列 or 裁剪窗口序列 遍历到一个intersection时，转换到另一个序列继续遍历，若发现某点已经遍历，即绘制多边形。

当出现回路时，回退到最后一个existing intersection

其中entering intersection为进入点，existing intersection 为退出点

当多边形序列遍历完毕后，算法结束

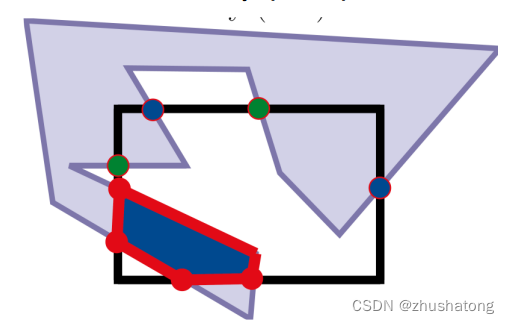
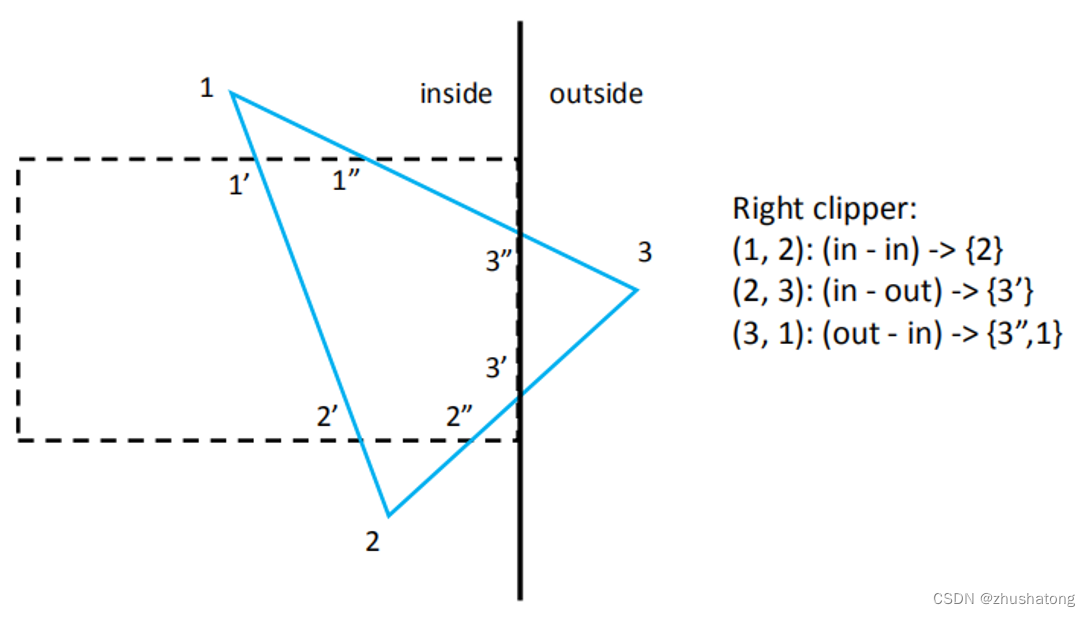
3.4 Sutherland-Hodgman Polygon Clipping

(in,in) / (in,out) / (out,in)

只要左边是in,一定输出一个点，且输出的点一定与右边数字有关，

Out,in 一定输出两个点，

Out out 输出None

Visible surface detection

Visibility of primitives:

primitive lies outside the field of the clipping volume

Primitive is back-facing

Primitive is occluded by one or more objects nearer the viewer

Visible surface algorithms

Object space technique:

applied before vertices are mapped to pixels

Back face culling , painter’s algorithm, BSP tree

Image space technique:

applied while the vertices are rasterized

Z Buffer

1 Back face culling

Face is visible iff θ∈[-90,90] culling faces --- should be hidden

Equivalently cos >= 0 or v ? n >= 0

2 Painter’s Algorithm

Render polygons a back to front order so that polygons behind others are simply painted over

3 BSP Tree (Binary space partitioning)

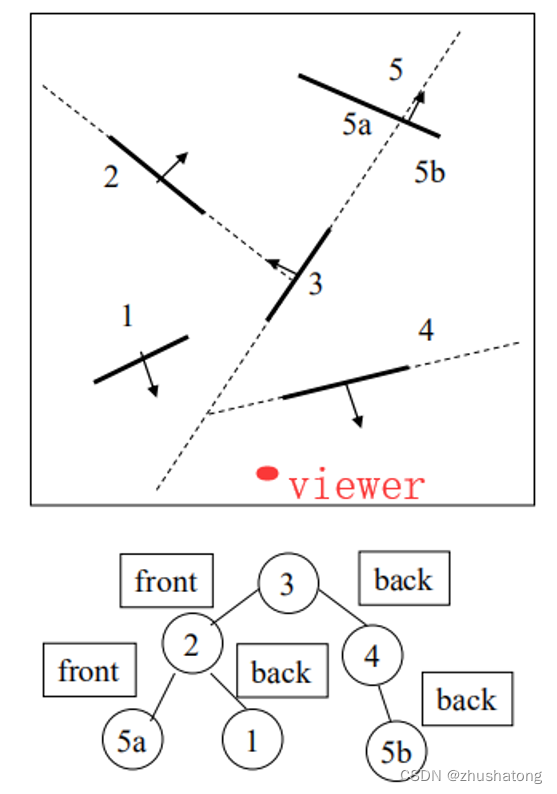
Traverse the tree, remember that we should paint the point according to the distance sort.

5a, 2, 1, 3, 5b, 4

4 Z-buffer complexity (n*m*k)

Rasterize every input polygon

Track depth values of closest polygon so far

Paint the pixel with the color of the polygon whose z value is the closest to the eye.

Advantage

? Simple to implement in hardware.

? Memory for z-buffer is now not expensive

? Diversity of primitives – not just polygons.

? Unlimited scene complexity

? Don’t need to calculate object-object intersections.

Disadvantage

? Extra memory and bandwidth

? Waste time drawing hidden objects

Z-precision errors

? May have to use point sampling

Frame buffer to save color information, depth buffer to save minimal depth information

When time to update the color, check whether current depth is less than saved depth.

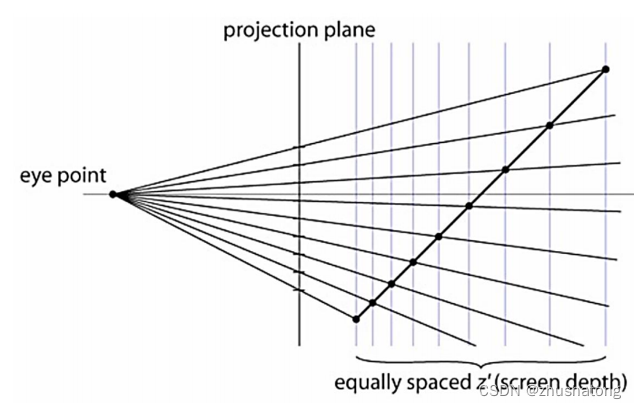
Z-buffer precision:（fighting）

Caused by the perspective division z/w when the interval is so small even come down to float-point precision.

push the zNear clipping plane out and pull the zFar plane in as much as possible

When far from projection plane, the resolution(分辨率) will enlarge, causing two closer primitive located in the same interval.

?如果这篇文章对你有帮助，欢迎点赞与收藏~