数据结构与算法教程,数据结构C语言版教程!(第三部分、栈(Stack)和队列(Queue)详解)一
?第三部分、栈(Stack)和队列(Queue)详解

栈和队列,严格意义上来说,也属于线性表,因为它们也都用于存储逻辑关系为 "一对一" 的数据,但由于它们比较特殊,因此将其单独作为一章,做重点讲解。
使用栈结构存储数据,讲究“先进后出”,即最先进栈的数据,最后出栈;使用队列存储数据,讲究 "先进先出",即最先进队列的数据,也最先出队列。
既然栈和队列都属于线性表,根据线性表分为顺序表和链表的特点,栈也可分为顺序栈和链表,队列也分为顺序队列和链队列,这些内容都会在本章做详细讲解。
一、什么是栈,栈存储结构详解
同顺序表和链表一样,栈也是用来存储逻辑关系为 "一对一" 数据的线性数据结构,如图 1 所示。

图 1 栈存储结构示意图
从图 1 我们看到,栈存储结构与之前所学的线性存储结构有所差异,这缘于栈对数据 "存" 和 "取" 的过程有特殊的要求:
- 栈只能从表的一端存取数据,另一端是封闭的,如图 1 所示;
- 在栈中,无论是存数据还是取数据,都必须遵循"先进后出"的原则,即最先进栈的元素最后出栈。拿图 1 的栈来说,从图中数据的存储状态可判断出,元素 1 是最先进的栈。因此,当需要从栈中取出元素 1 时,根据"先进后出"的原则,需提前将元素 3 和元素 2 从栈中取出,然后才能成功取出元素 1。
因此,我们可以给栈下一个定义,即栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构。
通常,栈的开口端被称为栈顶;相应地,封口端被称为栈底。因此,栈顶元素指的就是距离栈顶最近的元素,拿图 2 来说,栈顶元素为元素 4;同理,栈底元素指的是位于栈最底部的元素,图 2 中的栈底元素为元素 1。
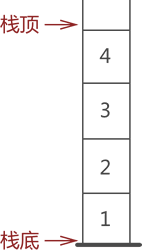
图 2 栈顶和栈底
1、进栈和出栈
基于栈结构的特点,在实际应用中,通常只会对栈执行以下两种操作:
- 向栈中添加元素,此过程被称为"进栈"(入栈或压栈);
- 从栈中提取出指定元素,此过程被称为"出栈"(或弹栈);
2、栈的具体实现
栈是一种 "特殊" 的线性存储结构,因此栈的具体实现有以下两种方式:
- 顺序栈:采用顺序存储结构可以模拟栈存储数据的特点,从而实现栈存储结构;
- 链栈:采用链式存储结构实现栈结构;
两种实现方式的区别,仅限于数据元素在实际物理空间上存放的相对位置,顺序栈底层采用的是数组,链栈底层采用的是链表。有关顺序栈和链栈的具体实现会在后续章节中作详细讲解。
3、栈的应用
基于栈结构对数据存取采用 "先进后出" 原则的特点,它可以用于实现很多功能。
例如,我们经常使用浏览器在各种网站上查找信息。假设先浏览的页面 A,然后关闭了页面 A 跳转到页面 B,随后又关闭页面 B 跳转到了页面 C。而此时,我们如果想重新回到页面 A,有两个选择:
- 重新搜索找到页面 A;
- 使用浏览器的"回退"功能。浏览器会先回退到页面 B,而后再回退到页面 A。
浏览器 "回退" 功能的实现,底层使用的就是栈存储结构。当你关闭页面 A 时,浏览器会将页面 A 入栈;同样,当你关闭页面 B 时,浏览器也会将 B入栈。因此,当你执行回退操作时,才会首先看到的是页面 B,然后是页面 A,这是栈中数据依次出栈的效果。
不仅如此,栈存储结构还可以帮我们检测代码中的括号匹配问题。多数编程语言都会用到括号(小括号、中括号和大括号),括号的错误使用(通常是丢右括号)会导致程序编译错误,而很多开发工具中都有检测代码是否有编辑错误的功能,其中就包含检测代码中的括号匹配问题,此功能的底层实现使用的就是栈结构。
同时,栈结构还可以实现数值的进制转换功能。例如,编写程序实现从十进制数自动转换成二进制数,就可以使用栈存储结构来实现。
以上也仅是栈应用领域的冰山一角,这里不再过多举例。在后续章节的学习中,我们会大量使用到栈结构。接下来,我们学习如何实现顺序栈和链栈,以及对栈中元素进行入栈和出栈的操作。
?二、顺序栈及基本操作(包含入栈和出栈)
顺序栈,即用顺序表栈存储结构。通过前面的学习我们知道,使用栈存储结构操作数据元素必须遵守 "先进后出" 的原则,本节就 "如何使用顺序表模拟栈以及实现对栈中数据的基本操作(出栈和入栈)" 给大家做详细介绍。
如果你仔细观察顺序表(底层实现是数组)和栈结构就会发现,它们存储数据的方式高度相似,只不过栈对数据的存取过程有特殊的限制,而顺序表没有。
例如,我们先使用顺序表(a 数组)存储?{1,2,3,4},存储状态如图 1 所示:

图 1 顺序表存储 {1,2,3,4}
同样,使用栈存储结构存储?{1,2,3,4},其存储状态如图 2 所示:
![]()
图 2 栈结构存储 {1,2,3,4}
通过图 1 和图 2 的对比不难看出,使用顺序表模拟栈结构很简单,只需要将数据从 a 数组下标为 0 的位置依次存储即可。
从数组下标为 0 的模拟栈存储数据是常用的方法,从其他数组下标处存储数据也完全可以,这里只是为了方便初学者理解。
了解了顺序表模拟栈存储数据后,接下来看如何模拟栈中元素出栈的操作。由于栈对存储元素出栈的次序有"先进后出"的要求,如果想将图 1 中存储的元素 1 从栈中取出,需先将元素 4、元素 3 和元素 2 依次从栈中取出。
这里给出使用顺序表模拟栈存储结构常用的实现思路,即在顺序表中设定一个实时指向栈顶元素的变量(一般命名为 top),top 初始值为 -1,表示栈中没有存储任何数据元素,及栈是"空栈"。一旦有数据元素进栈,则 top 就做 +1 操作;反之,如果数据元素出栈,top 就做 -1 操作。
1、顺序栈元素"入栈"
比如,还是模拟栈存储?{1,2,3,4}?的过程。最初,栈是"空栈",即数组是空的,top 值为初始值 -1,如图 3 所示:
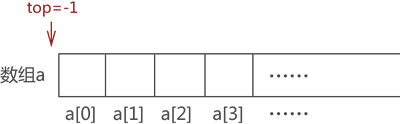
图 3 空栈示意图
首先向栈中添加元素 1,我们默认数组下标为 0 一端表示栈底,因此,元素 1 被存储在数组 a[1] 处,同时 top 值 +1,如图 4 所示:
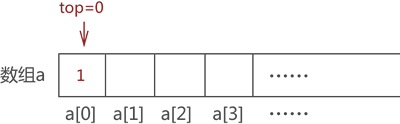
图 4 模拟栈存储元素 1
采用以上的方式,依次存储元素 2、3 和 4,最终,top 值变为 3,如图 5 所示:
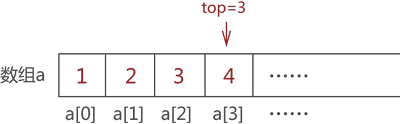
图 5 模拟栈存储{1,2,3,4}
因此,C 语言实现代码为:
//元素elem进栈,a为数组,top值为当前栈的栈顶位置
int push(int* a,int top,int elem){
????????a[++top]=elem;
????????return top;
}
代码中的 a[++top]=elem,等价于先执行 ++top,再执行 a[top]=elem。
2、顺序栈元素"出栈"
其实,top 变量的设置对模拟数据的 "入栈" 操作没有实际的帮助,它是为实现数据的 "出栈" 操作做准备的。
比如,将图 5 中的元素 2 出栈,则需要先将元素 4 和元素 3 依次出栈。需要注意的是,当有数据出栈时,要将 top 做 -1 操作。因此,元素 4 和元素 3 出栈的过程分别如图 6a) 和 6b) 所示:
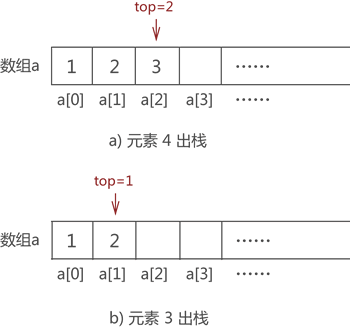
图 6 数据元素出栈
注意,图 6 数组中元素的消失仅是为了方便初学者学习,其实,这里只需要对 top 值做 -1 操作即可,因为 top 值本身就表示栈的栈顶位置,因此 top-1 就等同于栈顶元素出栈。并且后期向栈中添加元素时,新元素会存储在类似元素 4 这样的旧元素位置上,将旧元素覆盖。
元素 4 和元素 3 全部出栈后,元素 2 才能出栈。因此,使用顺序表模拟数据出栈操作的 C 语言实现代码为:
//数据元素出栈
int pop(int * a,int top){
????????if (top==-1) {
????????????????printf("空栈");
????????????????return -1;
????????}
????????printf("弹栈元素:%d\n",a[top]);
????????top--;
????????return top;
}
代码中的 if 语句是为了防止用户做 "栈中已无数据却还要数据出栈" 的错误操作。代码中,关于对栈中元素出栈操作的实现,只需要 top 值 -1 即可。
3、总结
通过学习顺序表模拟栈中数据入栈和出栈的操作,初学者完成了对顺序栈的学习,这里给出顺序栈及对数据基本操作的 C 语言完整代码:
#include <stdio.h>
//元素elem进栈
int push(int* a,int top,int elem){
????????a[++top]=elem;
????????return top;
}
//数据元素出栈
int pop(int * a,int top){
????????if (top==-1) {
????????????????printf("空栈");
????????????????return -1;
????????}
????????printf("弹栈元素:%d\n",a[top]);
????????top--;
????????return top;
????????}
int main() {
????????int a[100];
????????int top=-1;
????????top=push(a, top, 1);
????????top=push(a, top, 2);
????????top=push(a, top, 3);
????????top=push(a, top, 4);
????????top=pop(a, top);
????????top=pop(a, top);
????????top=pop(a, top);
????????top=pop(a, top);
????????top=pop(a, top);
????????return 0;
}
程序输出结果为:
弹栈元素:4
弹栈元素:3
弹栈元素:2
弹栈元素:1
空栈
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!