随机微分方程数值实验 数值解误差收敛阶(matlab)
2023-12-26 14:26:34
求解随机微分方程
实验结果如下:
1.当时
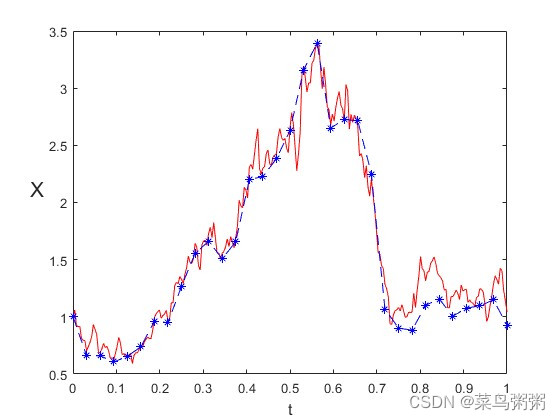
2.当时
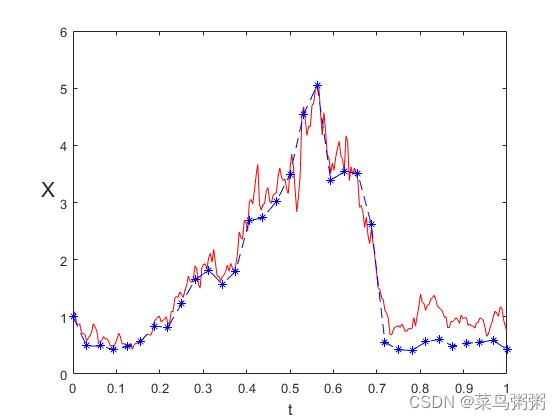
3.当时
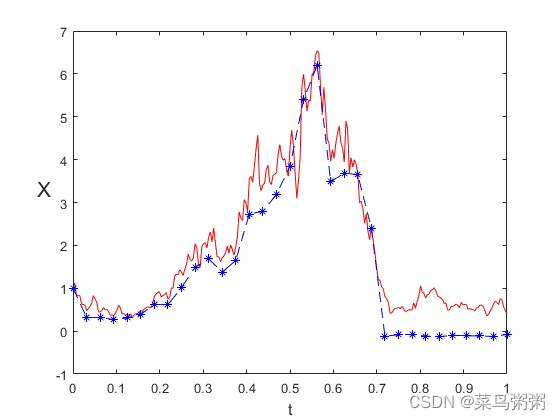
误差结果:

程序代码:
clear all;
randn('state',100)
%lambda=1;
%mu=1;
%lambda=1.5;
%mu=1.5;
lambda=2;
mu=2;
X_0=1;
T=1;
N=2^8;
dt=1/N;
dW=sqrt(dt)*randn(1,N);
W=cumsum(dW);
E_X=X_0*exp((lambda-0.5*mu^2)*([dt:dt:T])+mu*W);
plot([0:dt:T],[X_0,E_X],'r-');
hold on
R=8;
Dt=R*dt;
L=N/R;
X=zeros(1,L);
Xtemp=X_0;
for j=1:L
Winc=sum(dW(R*(j-1)+1:R*j));
Xtemp=Xtemp+Dt*lambda*Xtemp+mu*Xtemp*Winc;
X(j)=Xtemp;
end
E_X;
plot([0:Dt:T],[X_0,X],'b--*');
hold off
xlabel('t','FontSize',12);
ylabel('X','FontSize',16,'Rotation',0,'HorizontalAlignment','right');
error=abs(X(end)-E_X(end))
文章来源:https://blog.csdn.net/2301_76767110/article/details/135161537
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!