生存分析序章3——生存分析之Python篇：介绍生存分析和scikit-survival库

写在开头

在现代数据科学领域，生存分析是一项关键的统计方法，用于研究个体在一定时间内事件发生的概率。无论是医学、金融还是社会科学，生存分析都为我们提供了一种深入洞察数据的途径。在Python生态系统中，有一个强大的工具——scikit-survival库，专门用于处理生存分析问题。本篇博客将为您介绍生存分析的基本概念以及如何使用scikit-survival库进行生存分析，结合实际应用场景，揭示数据分析和数据挖掘中的潜在价值。

1. scikit-survival简介

1.1 生存分析的背景和应用领域

生存分析起源于医学领域，用于评估患者在特定治疗下的存活时间。随后，生存分析逐渐渗透到其他领域，如金融、社会科学和工程等，为我们理解事件发生背后的概率提供了强大工具。

1.2 scikit-survival库的作用和优势

scikit-survival是一个基于scikit-learn的库，专注于生存分析问题。其设计灵感来自R语言中的生存分析库，提供了丰富的功能和易于使用的API。在实际应用中，scikit-survival通过提供各种生存模型、评估工具和可视化函数，为数据科学家和分析师提供了便捷的工作环境。

2. 生存分析概述

2.1 生存函数、风险函数和累积风险函数的基本概念

• 生存函数（Survival Function）

  • 生存函数描述了在给定时间 t 内个体存活的概率。在医学研究中，可以用于估计患者在特定治疗下存活的可能性。例如，对于某个时间点 t，生存函数 S(t) 表示在该时间点之前个体存活的概率。

• 风险函数（Hazard Function）

  • 风险函数表示在给定时间 t 时发生事件的概率密度。在 Cox 比例风险模型中，风险函数的比率是模型的基本假设。通过观察风险函数的变化，我们可以了解事件发生的可能性在不同时间点的相对强度。

• 累积风险函数（Cumulative Hazard Function）

  • 累积风险函数是风险函数的积分，表示在给定时间 t 之前发生事件的累积概率。它是生存函数的负对数，通过观察累积风险函数的形状，我们可以了解事件的累积影响。

2.2 生存分析的应用场景和重要性

• 医学领域
  在医学领域，生存分析广泛应用于评估治疗效果、预测患者的生存时间。例如，可以通过生存分析确定新药对患者的疗效，并制定个体化的治疗计划。

• 金融领域
  在金融领域，生存分析可用于预测客户流失的可能性、评估贷款违约的风险。通过分析客户的生存曲线，金融机构可以更好地进行风险管理。

• 市场研究
  在市场研究中，生存分析可用于跟踪产品寿命、分析市场份额的变化。这有助于企业及时调整市场策略，确保产品在市场上的持续竞争力。

• 工程领域
  在工程领域，生存分析可用于预测设备的寿命，为维护计划提供支持。通过分析设备的失效时间，工程师可以制定更有效的维护策略，减少停机时间和维修成本。

生存分析的重要性在于它不仅提供了事件发生的概率预测，还允许我们理解事件如何随时间变化。这使得生存分析成为数据科学中一项强大而灵活的工具。

3. scikit-survival简介

3.1 scikit-survival库的基本信息

scikit-survival官网里有具体详细的信息，这里只会对基本的信息进行简单介绍。

支持的生存分析模型：

scikit-survival库支持多种生存分析模型，其中一些主要的模型包括：

• Kaplan-Meier 估计器： 用于估算生存函数，特别适用于处理右截尾的生存数据。

• Cox 比例风险模型： 用于估算协变量对风险的影响，是生存分析中最常用的模型之一。

• 加速失效时间模型（AFT）： 用于估计事件发生时间的概率分布，适用于非比例风险的情况。

• 支持向量机生存模型： 利用支持向量机的方法进行生存分析，对于复杂数据集具有较好的拟合能力。

API的一致性

scikit-survival库的API设计与scikit-learn类似，这使得用户在熟悉scikit-learn的基础上更容易上手。同时，它充分利用了scikit-learn的交叉验证、网格搜索等功能，使得模型的训练和评估更加方便。

与Pandas的兼容性

scikit-survival库与Pandas数据结构兼容，这意味着用户可以直接使用Pandas的DataFrame作为输入，无需进行繁琐的数据格式转换。

3.2 安装和环境设置

为了安装scikit-survival库，可以使用以下命令：

pip install scikit-survival

如果安装有conda的话，可以使用下面的命令：

conda install -c sebp scikit-survival

此外，为了获得最佳性能，推荐安装一些加速库，例如Cython和OpenBLAS。安装完成后，您可以在Python环境中导入scikit-survival，并开始使用其中提供的多种生存分析模型。

import sksurv

通过这些特性，scikit-survival库为用户提供了强大而灵活的工具，支持多种生存分析模型，并使得整个建模过程更加便捷。

4. 基本功能演示

4.1 使用scikit-survival进行生存数据的加载和预处理

在生存分析中，数据的准备和预处理是至关重要的一步。首先，我们需要加载生存数据集。scikit-survival支持多种数据格式，包括Pandas DataFrame和NumPy数组。下面是一个简单的示例，演示了如何加载数据集并查看前几行数据：

import pandas as pd
from sksurv.datasets import load_whas500

# 加载WHAS500数据集
data = load_whas500()
df = pd.DataFrame(data['data'])
print(df.head())

运行上述代码后，其结果如下：

下面是对上述数据的一些说明：

字段名称	英文注释	中文注释	数值解释
id	Identification Number	识别号	1 - 500
afb	Atrial Fibrillation	心房颤动	0 = No, 1 = Yes
age	Age at Hospital Admission	住院年龄	Years
av3	Complete Heart Block	完全心脏传导阻滞	0 = No, 1 = Yes
bmi	Body Mass Index	身体质量指数	kg/m^2
chf	Congestive Heart Complications	充血性心脏并发症	0 = No, 1 = Yes
cvd	History of Cardiovascular Disease	心血管疾病病史	0 = No, 1 = Yes
diasbp	Initial Diastolic Blood Pressure	初始舒张压	mmHg
gender	Gender	性别	0 = Male, 1 = Female
hr	Initial Heart Rate	初始心率	Beats per minute
los	Length of Hospital Stay	住院时间	Days from Hospital Admission to Hospital Discharge
miord	MI Order	MI订单	0 = First, 1 = Recurrent
mitype	MI Type	MI类型	0 = non Q-wave, 1 = Q-wave
sho	Cardiogenic Shock	心源性休克	0 = No, 1 = Yes
sysbp	Initial Systolic Blood Pressure	初始收缩压	mmHg
fstat	Vital Status at Last Follow-up	最后一次随访时的重要状态	0 = Alive, 1 = Dead
lenfol	Total Length of Follow-up	随访总长度	Days from Hospital Admission Date to Date of Last Follow-up

接下来，我们可能需要处理缺失值。在生存分析中，通常采用一些特殊的处理方式，例如使用中位数来填充缺失的生存时间。以下是一个简单的例子：

# 填充缺失的生存时间（Survival Time）列
median_survival_time = df['lenfol'].median()
df['lenfol'].fillna(median_survival_time, inplace=True)

4.2 利用库中的生存分析工具生成生存曲线和风险函数

在数据预处理完成后，我们可以使用scikit-survival库的生存分析工具来生成生存曲线和风险函数。以下是一个基本的演示，使用Kaplan-Meier估计器绘制生存曲线：

import matplotlib.pyplot as plt
from sksurv.nonparametric import kaplan_meier_estimator

# 建立模型
time, survival_prob, conf_int = kaplan_meier_estimator(
    df['fstat'], df['lenfol'],  conf_type="log-log"
)

# 绘制图像
plt.step(time, survival_prob, where="post")
# 添加置信区间
plt.fill_between(time, conf_int[0], conf_int[1], alpha=0.25, step="post")
plt.ylim(0, 1)
plt.ylabel(r"est. probability of survival $\hat{S}(t)$")
plt.xlabel("time $t$")

上述代码中，lenfol是生存时间，status是事件发生标志。通过Kaplan-Meier估计器，我们得到了生存曲线的图形:

同样，我们可以使用Nelson-Aalen估计器绘制风险函数图，该图展示了随时间变化的事件发生率。以下是一个简单的例子：

from sksurv.nonparametric import nelson_aalen_estimator


# 拟合风险函数
event_times,cumulative_hazard = nelson_aalen_estimator(df['fstat'], df['lenfol'])

# 绘制风险函数图
plt.step(event_times, cumulative_hazard, where="post")
plt.title("Nelson-Aalen Cumulative Hazard Function")
plt.xlabel("Time")
plt.ylabel("Cumulative Hazard")
plt.show()

运行上述代码，得出对应的风险累计图：

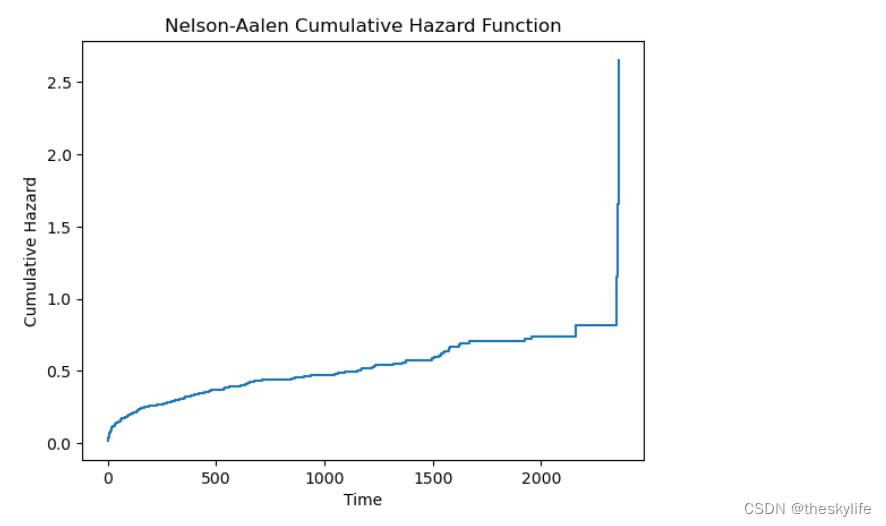
这两个示例演示了如何使用scikit-survival库进行基本的生存分析，包括数据加载、预处理以及生存曲线和风险函数的绘制。在实际应用中，根据数据的特点和问题的复杂性，我们可以进一步选择和调整模型，以更准确地进行生存分析。

写在最后

通过本文，我们初步了解了生存分析的基本概念，并深入介绍了scikit-survival库的使用。生存分析在数据分析和数据挖掘中具有重要价值，帮助我们更好地理解事件发生的概率和规律。在接下来的文章中，我们将深入探讨生存分析的更多高级主题，并结合实际案例展示其在不同领域的应用。希望本文为您打开了生存分析之门，让您能够更加灵活地应用这一强大的工具解决实际问题。