Think-on-Graph—基于知识图谱的LLM推理

背景

由IDEA研究院、微软亚洲研究院、香港科技大学等多方研究团队合作推出的 Think-on-Graph 技术，在深度推理领域掀起了一场革新。

为了解决大模型在金融、法律、医疗等垂直领域的幻觉问题，Think-on-Graph采用了紧耦合的新范式，将大模型作为 agent 与知识图谱相互协作。这一方法不仅使推理过程更加清晰有序，还提供了可追溯的推理链条。通过具体的例子，对比了传统大模型在推理问题上的表现及 Think-on-Graph 的方式，突显了其在逻辑分析和推理透明度方面的优势。Think-on-Graph 被证明在多个基准数据集上实现了巨大的性能提升，刷新了相关领域的性能榜单。

论文地址：https://arxiv.org/pdf/2307.07697.pdf
代码链接：https://github.com/IDEA-FinAI/ToG

动机

LLM模型存在的问题

尽管大型语言模型（LLM）在各种自然语言处理任务中都取得了显著的成功，但它面临以下几个问题：

• 首先，LLM通常无法准确回答需要预训练阶段以外的专业知识的问题（例如图1(a)中的过时知识），或需要长逻辑链和多跳知识推理的问题（即复杂的知识推理任务）；
• 其次，LLM缺乏责任感、可解释性和透明度，这增加了用户对“幻觉生成”和“有害文本”风险的担忧；
• 第三，LLM的训练过程通常既昂贵又耗时，这使得它们很难保持最新的知识。

认识到这些挑战，一个自然而有前景的解决方案是结合外部知识，如知识图谱（KGs），以帮助改进LLM推理。KGs提供结构化、明确和可编辑的知识表示，提供了一种互补的策略来减轻LLM的局限性。

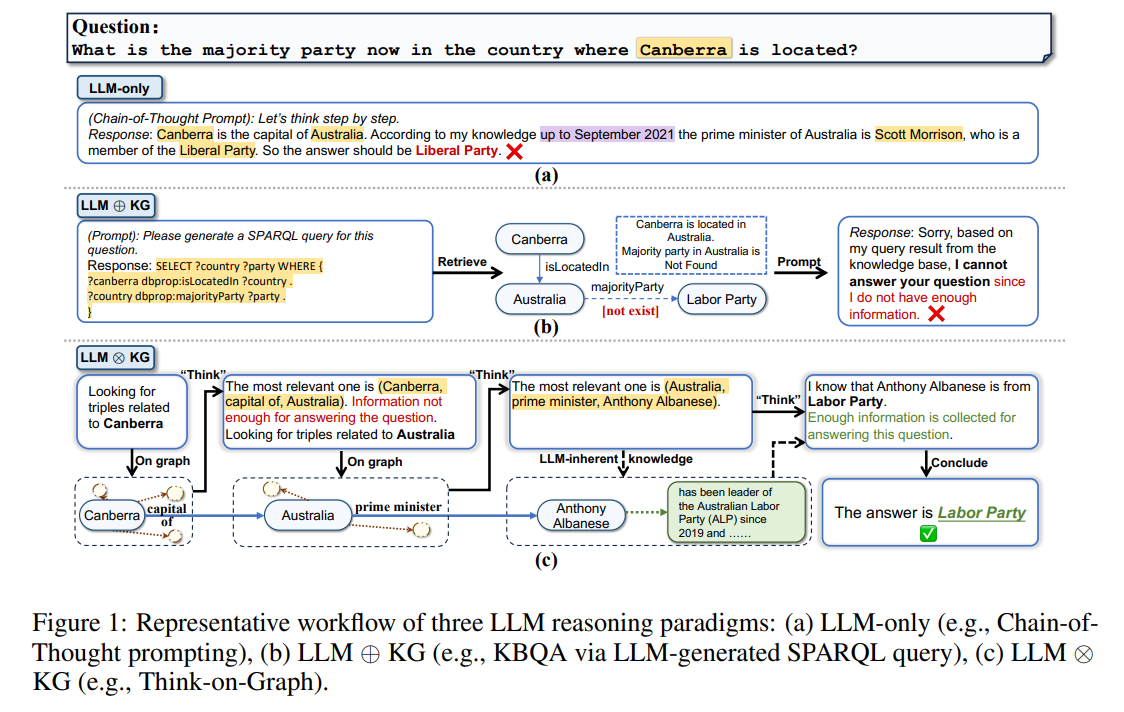
问题：
现在堪培拉所在的国家中，哪个党派占据多数？
答：回答：堪培拉是澳大利亚的首都。根据我截至2021年9月的知识，澳大利亚的总理是斯科特·莫里森，他是自由党成员。所以答案应该是自由党。

SPARQL是一种RDF查询语言，专门用于访问和操作RDF数据。
RDF：Resource Description Framework， 资源描述框架。大部分知识图谱使用RDF描述世界上的各种资源，并以三元组的形式保存到知识库中。RDF提出了一个简单的二元关系模型来表示事物之间的语义关系，即使用三元组集合的方式来描述事物和关系。三元组是知识图谱中知识表示的基本单位，简称SPO，三元组被用来表示实体与实体之间的关系,或者实体的某个属性的属性值是什么。

LLM$\oplus$KG范式的局限性

已经有不少工作探索了使用KGs作为外部知识源来减轻LLMs的幻觉问题，这些方法通常的做法是：从KGs中检索信息，相应地增加提示，并将增加的提示输入LLMs（如图1b所示）。尽管这类方法旨在整合LLM和KG的能力，但在这种范式中，LLM仅扮演着翻译器的角色，将输入问题转换为机器可理解的SPARQL命令，用于KG的搜索和推理，但它并不直接参与知识图谱的推理过程。这样的缺点是，松散耦合的LLM$\oplus$KG范式有其自身的局限性，其成功在很大程度上取决于KG的完整性和高质量。例如，在图1b中，尽管LLM成功地确定了回答问题所需的必要关系类型，但因为缺乏关系“majority party”，导致最终没有正确检索到答案。

LLM$?$KG范式（Think on Graph，ToG）

本文提出了一种新的紧耦合“LLM?KG”范式，其中KG和LLM协同工作，在图推理的每一步中互补彼此的能力。图1?提供了一个示例，说明LLM?KG的优势。在本例中，导致图1b中失败的缺失关系“majority party”可以由具有动态推理能力的LLM agent发现的参考三元组（Australia, prime minister, Anthony Albanese）、以及来自 LLM 固有知识的 安东尼阿尔巴尼斯的政党成员身份来补充。通过这种方式，LLM成功地利用从KGs检索到的可靠知识生成了正确的答案。

LLM$?$KG范式的过程

Think-on-Graph(ToG)，意思是LLM沿着图"思考"，也就是LLM沿着推理路径"在"知识图谱"上逐步"思考"。（step by step）

ToG 通过要求LLM对知识图谱执行集束搜索来实现“LLM?KG”范式。具体来说，它提示LLM迭代地探索KGs上的多个可能的推理路径，直到LLM确定可以根据当前推理路径回答问题。

集束搜索：beam search有一个超参数beam size（束宽），设为 k。第一个时间步长，选取当前条件概率最大的k个词，当做候选输出序列的第一个词。之后的每个时间步长，基于上个步长的输出序列，挑选出所有组合中条件概率最大的 k 个，作为该时间步长下的候选输出序列。始终保持k个候选。最后从k个候选中挑出最优的。

该算法为一个可循环的迭代过程，每次循环需先后完成搜索剪枝、推理决策两个任务，搜索剪枝用于找出最有希望成为正确答案的推理路径，推理决策任务则通过LLM来判断已有的候选推理路径是否足以回答问题，如果判断结果为否，则继续迭代到下个循环。

在ToG之外，ToG-R根据实体搜索得到的以EDcand结尾的所有候选推理路径执行推理步骤。与ToG相比，ToG-R省去了使用LLM修剪实体的过程，从而降低了总体成本和推理时间，并且强调关系的字面信息，当中间实体的字面信息缺失或不为LLM所熟悉时，可以降低误导推理的风险。

ToG的三个阶段

ToG 在每次迭代后，不断更新和维护问题 $x$ 的前 $N$ 条推理路径 $P=p_1,p_2,\dots ,p_N$，其中 $N$ 表示波束搜索的宽度。ToG 的整个推理过程包括以下三个阶段：初始化、探索和推理。

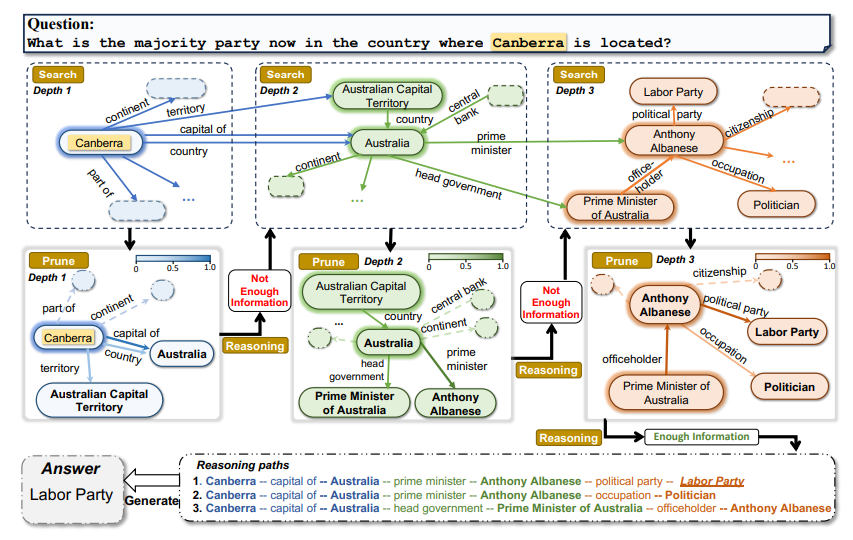
图2.ToG 的示例工作流程。高亮实体是在每次迭代（depth）开始搜索的中心实体，粗体的实体是修剪后下一次迭代的选定中心实体。在每个修剪步骤中，边缘的深浅表示LLM给出的排序分数，虚线表示由于低评估分数而被修剪的关系。

因此，这个时候的核心，就在于怎么选择中心实体，以及怎么进行边的排序从而实现剪枝。

初始化实体提取

给定问题后，ToG利用底层LLM定位知识图谱上推理路径的初始实体。这一阶段可视为前$N$ 个推理路径 $P$ 的初始化。ToG首先会提示LLM自动提取问题中的主题实体，并得到问题的前 $N$ 个主题实体$E^0=e_1^0,e_2^0,\dots ,e_N^0$，主题实体的数量可能少于 $N$。

关系及实体探索

在第 $D$ 次迭代开始时，每条路径 $p_n$ 由 $D?1$ 个三元组组成，即:
$p_n={\left\{\left(e_{s,n}^d,r_{j,n}^d,e_{o,n}^d\right)\right\}}_{d=1}^{D?1}$ ，其中 $e_{s,n}^d$ 和 $e_{o,n}^d$ 分别表示主体实体和客体实体， $r_{j,n}^d$ 是它们之间的特定关系。 $\left(e_{s,n}^d,r_{j,n}^d,e_{o,n}^d\right)$ 和 $\left(e_{s,n}^{d+1},r_{j,n}^{d+1},e_{o,n}^{d+1}\right)$ 彼此连接。 $P$ 中的尾实体和关系分别表示为: $E^{D?1}=e_1^{D?1},e_2^{D?1},\dots ,e_N^{D?1}$ 和 $R^{D?1}=r_1^{D?1},r_2^{D?1},\dots ,r_N^{D?1}$ 。

关系探索

关系探索是从 $E_{D?1}$ 到 $R_D$ 的深度为1、宽度为 $N$ 的集束搜索过程。整个过程可以分解为两个步骤：搜索和修剪。LLM充当自动完成此过程的agent。

• 搜索: 在第 $\mathrm{D}$ 次迭代开始时，关系探索阶段首先为每个推理路径 $p_n$ 搜索链接到尾部实体 $e_n^{D?1}$的关系 $R_{cand,n}^D$ 。这些关系被聚合为 $R_{cand}^D$ 。在图2的情况下， $E^1=$ Canberra， $R_{cand}^1$表示与 Canberra 内部或外部相关的所有关系的集合。

• 修剪: 一旦我们从关系搜索中获得了候选关系集 $R_{cand}^D$ 和扩展的候选推理路径 $P_{cand}$ ，我们就可以利用LLM基于问题 $x$ 的文字信息和候选关系 $R_{cand}^D$ 从 $P_{cand}$ 中选择出以尾部关系 $R^D$ 结尾的新的前 $N$ 个推理路径 $P$ 。如图2所示，LLM在第一次迭代中从与实体 Canberra 相关的所有关系中选择前三个关系{capital of, country, territory }。由于 Canberra 是唯一的主题实体，排名前三的候选推理路径更新为 { \{ { (Canberra， capital of),(Canberra， country),(Canberra， territory)}。

实体探索

实体探索与关系探索类似，实体探索也是LLM从 $R^D$ 到 $E^D$ 执行的集束搜索过程，也由搜索和修剪两个步骤组成。

• 搜索: 一旦我们从关系探索中获得了新的前 $N$ 个推理路径 $P$ 和一组新的尾部关系 $R^D$ ，对于每个关系路径 $p_n\in P$ ，我们可以通过查询 $\left(e_n^{D?1},r_n^D,?\right)$ 或 $\left(?,r_n^D,e_n^{D?1}\right)$ 来探索候选实体集 $E_{cand,n}^D$ ，其中 $e_n^{D?1},r_n$ 表示 $p_n$ 的尾部实体和关系。我们可以将
  $E_{cand,1}^D,E_{cand,2}^D,\dots ,E_{cand,2}^D$ 聚合到 $E_{cand}^D$ 中，并将前 $N$ 条推理路径 $P$ 扩展到具有尾部实体 $E_{cand}^D$ 的 $P_{cand}$ 。对于所示的情况， $E_{cand}^1$ 可以表示为 { \{ { Australia, Australia, Australian Capital Territory}。
• 修剪: 由于每个候选集合 $E_{cand}^D$ 中的实体是用自然语言表示的，因此我们可以利用LLM来选择新的前 $N$ 个推理路径 $P$ ，该路径 $P$ 以 $P_{\text{cand?}}$ 的尾部实体 $E^D$ 结束。如图2所示，Australia 和Australian Capital Territory的得分为1，因为，国家和领地的关系资本分别只与一个尾部实 Australia),(Canberra, territory, Australian Capital Territory)}。

在执行上述两个探索之后，我们重建新的前 $N$ 条推理路径 $P$ ，其中每条路径的长度增加 1 。每个修剪步骤最多需要 $N$ 个LLM调用。

推理

在通过探索过程获得当前推理路径 $P$ 后，我们提示LLM评估当前推理路径是否足以生成答案。如果评估结果为肯定，我们将提示LLM使用推理路径生成答案，并将查询作为输入，如图2所示。相反，如果评估结果为阴性，我们重复探索和推理步骤，直到评估结果为阳性或达到最大搜索深度 $D_{\text{max?}}$ 。如果算法尚未结束，则表明即使达到 $D_{\text{max?}}$ ，ToG仍然无法探索解决问题的推理路径。在这种情况下，ToG仅基于LLM中的固有知识生成答案。ToG的整个推理过程包括 $D$ 个探索阶段和 $D$ 个评估步骤以及一个生成步骤，该生成步骤最多需要对LLM进行 $2ND+D+1$ 次调用。

例子及效果

一个具体的例子，给定问题，得到推理路径，生成答案。

不同数据集上 ToG 的效果

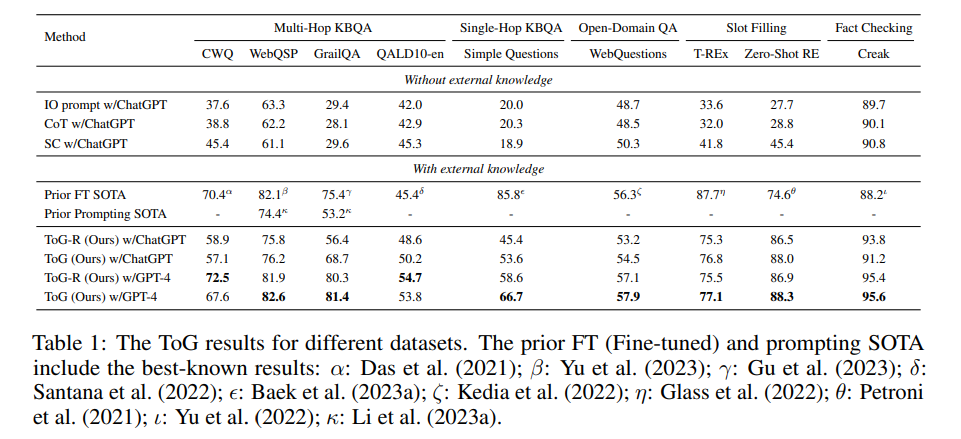
相关结论

搜索深度和波束宽度对ToG性能的影响

为了探索搜索深度Dmax和波束宽度N对ToG性能的影响，该工作在深度为1到4和宽度为1到4的设置下进行了实验。

如图3所示，ToG的性能随着搜索深度和宽度的增加而提高。这也意味着ToG的性能有可能随着探索深度和广度的增加而提高。【这个跟问题是否多跳有很大关系】

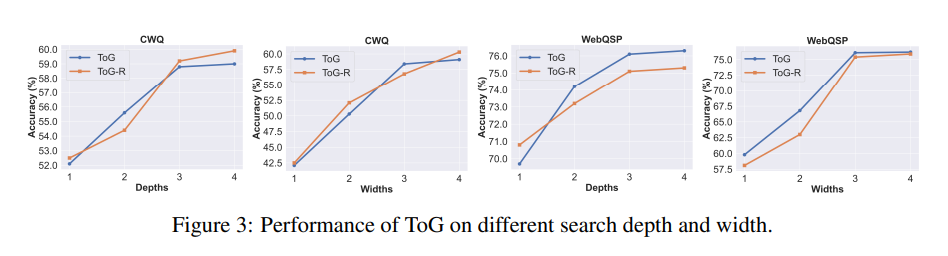
另一方面，当深度超过3时，性能增长就会减弱。这主要是因为只有一小部分问题的推理深度（基于SPARQL中的关系数，大于3。

不同的提示设计对ToG性能的影响

为了探究不同的提示设计对ToG的影响，需要确定哪种类型的提示表示法更为实用。实验结果见表4。

其中：“Triplet"表示使用三重格式作为提示来表示多个路径，如”（堪培拉，澳大利亚首都），（澳大利亚，总理，安东尼-阿尔巴内斯）"。

"sequence"是指使用序列格式，如图2所示。

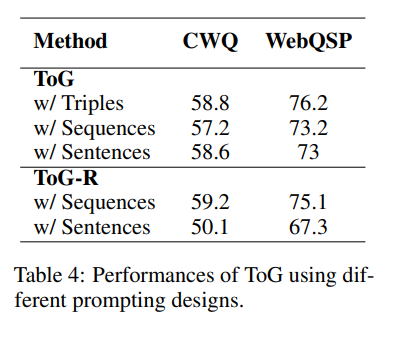
“sentence"涉及将三元组转换为自然语言句子。例如，”（堪培拉，澳大利亚首都）“可转换为"堪培拉的首都是澳大利亚”。

结果表明，在推理路径中使用基于三元组的表示法能产生最高的效率和最好的性能。

相反，在考虑ToG-R时，每条推理路径都是以主题实体为起点的关系链，因此与基于triple的提示表示法不兼容。因此，将ToG-R转换为自然语言形式会导致提示过于冗长，从而导致性能明显下降。

不同剪枝工具的影响

不同剪枝工具的影响。除了LLM之外，像BM25和SentenceBERT这样能确保文本相似性的轻量级模型也可以在探索阶段用作剪枝工具。

例如，可以根据实体和关系与问题的字面相似性来选择前N个实体和关系。对ToG性能的影响，如表5所示。使用BM25或SentenceBERT替代LLM会导致性能显著下降。

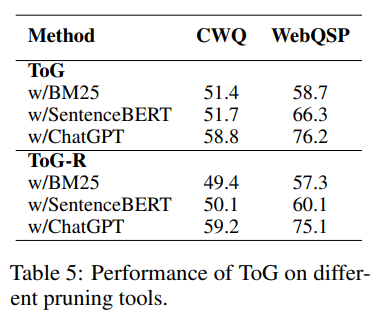
不过，在使用BM25或SentenceBERT后，可以有效减少调用LLM的次数。

种子示例数量的敏感性

种子示例数量的敏感性。为了更好地了解ToG对种子示例数量的敏感性，该工作进行敏感性分析。

具体地，在fewshot试验的基础上，并从训练集中选择了1-6个示例作为fewshot试验设置。在Fewshot测试中，随机选择{1,2,3,4,6}个示例中的M个作为示例，并重复实验三次。随着示例数量的增加，整体性能也普遍提高。