论文笔记:Accurate Localization using LTE Signaling Data
2023-12-20 23:55:49
1 intro
- 论文提出LTELoc,仅使用信令数据实现精准定位
- 信令数据已经包含在已在LTE系统中,因此这种方法几乎不需要数据获取成本
- 仅使用TA(时序提前)和RSRP【这里单位是瓦】(参考信号接收功率)
- TA值对应于信号从手机到达基站所需的时间长度
- ——>考虑到光速,它相当于用户设备与基站之间的距离
- 在4G LTE网络中,TA值介于0到63之间,每个步骤代表一个比特周期(大约0.5208μs)的提前。
- 以大约3×10^8米/秒的速度传播的无线电波,一个TA步长则代表大约156.24米的往返距离变化。
- 这意味着,每当移动设备与基站之间的距离变化78.12米,TA值就会变化。
- RSRP定义为在考虑的测量频带宽度内,特定参考信号的功率贡献的平均值
- TA值对应于信号从手机到达基站所需的时间长度
- 与传统的基于蜂窝的方法(如使用RSSI(接收信号强度指示))相比,LTELoc更准确
- LTE小区通常具有具有120度扇区化天线的定向基站发射器
- 给定一个服务小区的TA值,用户可以位于阴影区域的任何位置。
- 特别是当TA较大时(这意味着用户距离基站较远),这个区域会很大。

- 为了提供高精度的基于蜂窝的定位,论文将TA和RSRP的组合作为一个指纹(fingerprint)
- TA作为距离指示器,而RSRP作为角度信息
- 可以预期在一个小区域内只能看到一个独特的指纹
- 考虑(TA, RSRP)签名序列,并执行地图匹配过程来提高定位精度
2 Preliminary
2.1 TA和RSRP
2.1.1 TA和RSRP的稳定性
- 论文首先展示TA和RSRP相对稳定,因此是定位的良好签名
- 为了验证这一点,论文检查相同位置收集相同cell信号的TA和RSRP是否相同
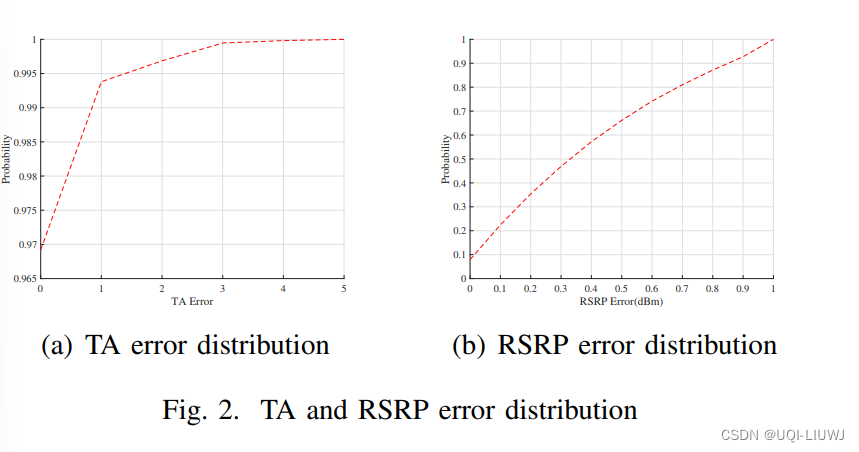
- 图2(a)显示了TA误差分布的累积分布函数(CDF),可以看到超过99%是正确的。
- 图2(b)显示了RSRP误差分布的CDF,可以看到几乎所有的误差都小于1 dBm。
2.1.2 一个指纹数据
- 使用
和
分别表示时间t时来自小区k的TA/RSRP。一个指纹是
。与LTELoc相关的数据有两种:
- 训练数据:
- 从道路网络中的一组位置收集的带有地理标签的数据。
- 给定了n个位置
,以及每个位置服务小区k的
和
。
- 观测数据:
- 这些数据没有地理标签,但带有时间戳。
- 确切地说,对于每个移动设备,给定时间实例ti,i = 1, 2, ..., T,对于每个ti,我们给定
和
。
- 训练数据:
2.2 问题定义
- 考虑一个有K个小区的LTE网络。一个移动设备在由图G = (V,E)表示的道路网络中行驶,其中V表示由纬度-经度元组特征化的节点,E表示两个节点之间的有向边。
- 给定一系列(
,
)观测值,估计用户位置。
3 模型
3.0 模型整体架构
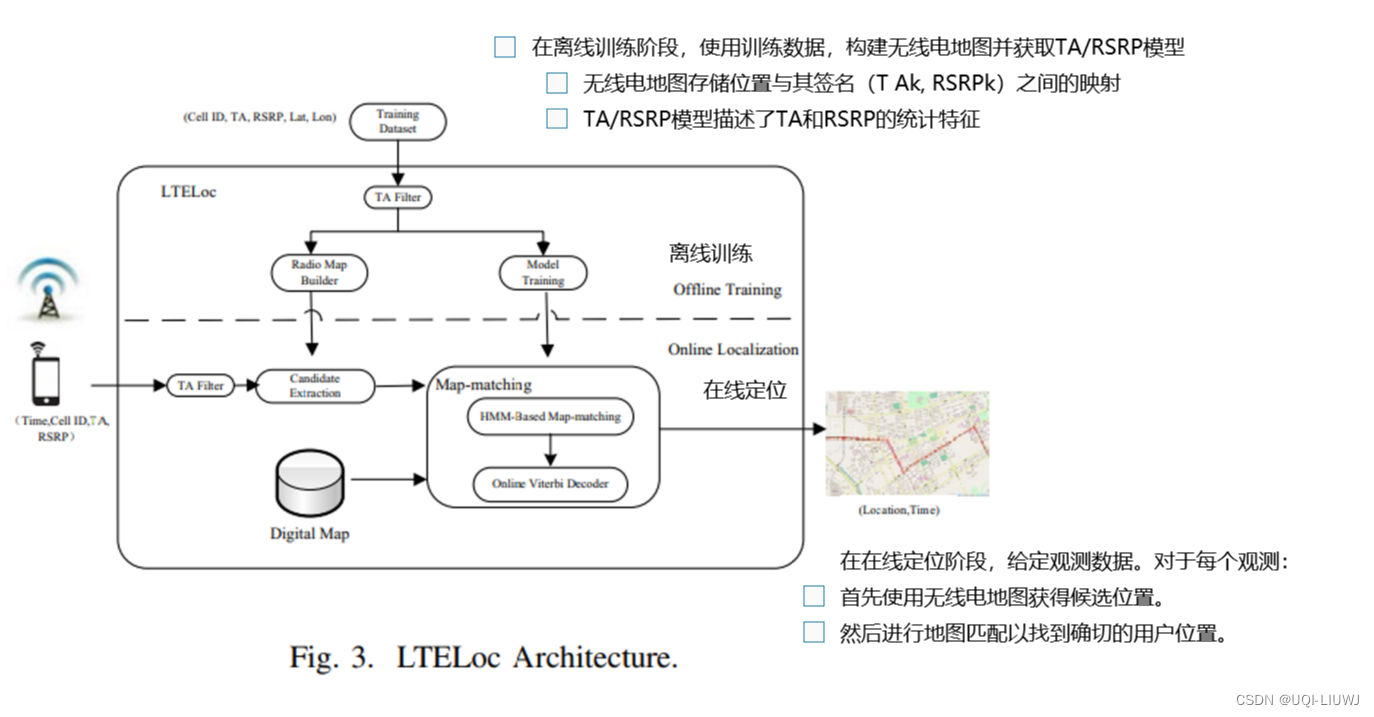
3.1 地图匹配
3.1.1 HMM模型
- λ = (X, F, A, B, π)
- X = (x1, x2, ..., xN) 是隐藏状态的集合,N = |X|
- 每个可能的状态代表道路段上的一个点(纬度-经度)
- F = (F1, F2, ..., FM) 是观测集合,M = |F|
- 每个观测是
- 每个观测是
- A = [aij] 是转移概率矩阵
- aij = p(xi → xj),1 ≤ i, j ≤ N
- B = [bij] 是观测概率矩阵
- bij = p(Fj |xi),1 ≤ i ≤ N, 1 ≤ j ≤ M
- π = {πi} 是初始状态分布
- πi = p(xi)
- X = (x1, x2, ..., xN) 是隐藏状态的集合,N = |X|
3.1.2 获取某一个fingerprint的候选点
- 给定一个fingerprint?
,选择如下的点作为候选点:
- 连接着小区k的点
- TA ∈ [T Ak(t) - 1, T Ak(t) + 1]
- RSRP ∈ [RSRPk(t) - 1dB, RSRPk(t) + 1dB]
3.1.3 获取观测概率p(Fj |xi)
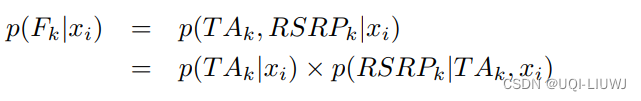
- 计算
- 在某个TAk值附近,可能存在多个候选位置。
- 在缺乏其他信息的情况下,论文做了一个均等可能性的假设:这个TAk值附近的所有位置是等可能的
- 也即每个候选点位置xi产生观测值T Ak的概率是相同的
- 记TAk的候选点数量为N,则
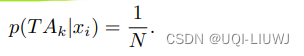
- 计算p(RSRPk∣TAk,xi)
- 为了计算在给定TA值和位置的情况下观测到特定RSRP值的概率,采用了SVM
- 数据收集:
- 首先,从每个小区收集数据,这些数据应包括在不同位置测得的TA和RSRP值。
- SVM模型训练:
- 使用这些数据来训练一个SVM模型。
- 在这个模型中,TA值和位置信息(纬度和经度)被用作特征,而RSRP值的统计数据(平均值)是模型的输出。
- SVM模型能够对新的输入数据(即TA值和位置)预测RSRP值。
- 概率估计:
- 使用SVM模型【支持向量回归SVR】来预测在给定TA值时,在某一特定位置xi的RSRP的平均值。
- 然后假设RSRP值在这一位置呈正态分布,其中SVM预测的RSRP值是均值,标准差σk? 是从数据中得到的。
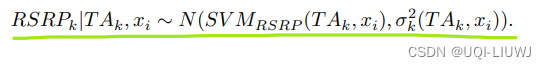
- 数据收集:
- 为了计算在给定TA值和位置的情况下观测到特定RSRP值的概率,采用了SVM
3.1.4 获取转移概率p(xi → xj)

表示修正后的距离
- 假设在从位置xi到xj的过渡过程中,有c次道路切换,那么修正后的距离为
- δ是道路切换的惩罚
3.1.5 维特比算法
获得输出概率和转移概率后,目标就是最大化:
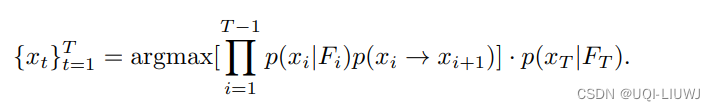
类似于HMM ,使用维特比算法
4 实验
4.1 多少比例用作training?
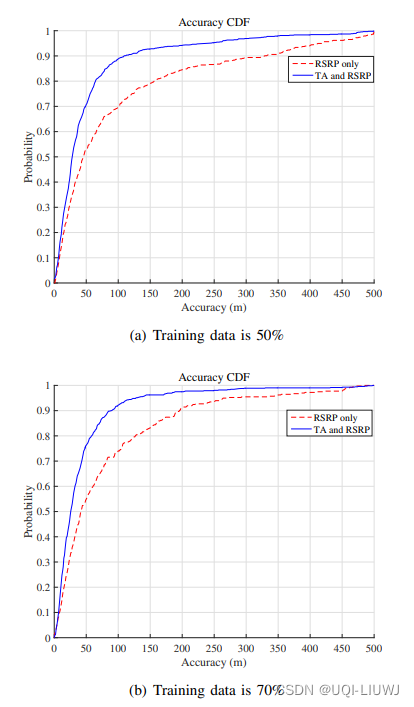
文章来源:https://blog.csdn.net/qq_40206371/article/details/135111319
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!