回溯算法第一篇（子集树问题【三种思路】、0-1背包问题、最小重量机器设计问题）

目录

1. 子集树问题

解法一

解法二

解法三

2. 0-1背包问题（使用子集树解决）

3.?最小重量机器设计问题

---

1. 子集树问题

子集力扣链接

题目描述：给你一个整数数组?nums?，数组中的元素?互不相同?。返回该数组所有可能的子集（幂集）。解集?不能?包含重复的子集。你可以按?任意顺序?返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums?中的所有元素?互不相同

注：子集是不能重复的，例如{1,2,3}和{3,2,1}是一个子集。

解决方案如下：

解法一

算法策略为判断当前位置选还是不选，则决策树的形状是二叉树，决策树如下：

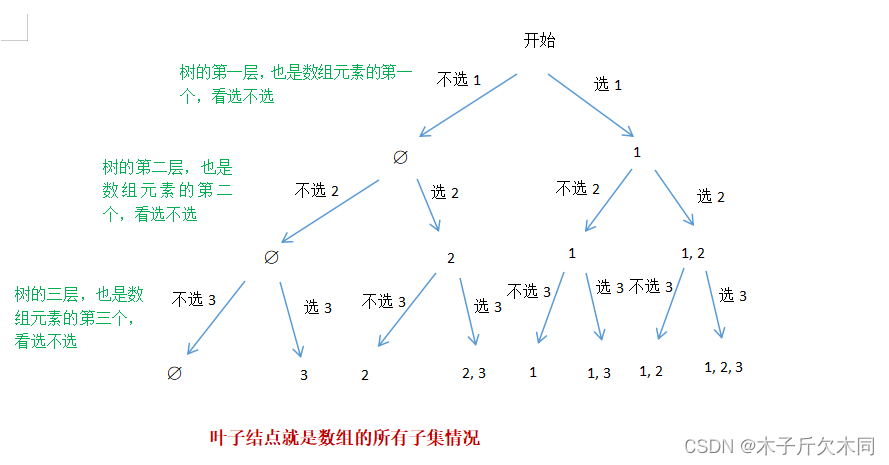
注：以下代码不是力扣那道题的正确代码，需要自行修改一些方法名，解法二的代码就可以在力扣运行且通过所有测试

import java.util.ArrayList;
import java.util.List;
//子集的第一种结果：叶子结点收集
public class SubsetTest {
    //设计全局变量
    static List<Integer> path;//用来临时接受一次自己的情况
    static List<List<Integer>> ret;//用来接收全部子集情况

    //nums：表示需要计算子集的数组
    //deep：表示第几层，也是表示nums数组的第几个元素，有两种选择，选还是不选
    public static void permute(int[] nums, int deep) {
        //1.初始化
        path = new ArrayList<>();
        ret = new ArrayList<>();
        //2.开始进行回溯算法
        dfs(nums, deep);
    }

    public static void output() {
        ret.add(new ArrayList<>(path));
    }

    public static void dfs(int[] nums, int deep) {
        //递归出口
        if (deep == nums.length) {
            output();
            return;
        } else {//这回溯的核心写成决策树，是一颗二叉树，因为有两种选择
            //（1）选
            path.add(nums[deep]);
            //进入下一层
            dfs(nums, deep + 1);
            //恢复现场：移除最后一个元素
            path.remove(path.size() - 1);

            //（2）不选，因为不选没有改变path集合，所以不需要恢复现场
            dfs(nums, deep + 1);
        }
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        permute(nums, 0);
        for (int i = 0; i < ret.size(); i++) {
            System.out.println(ret.get(i));
        }
    }
}

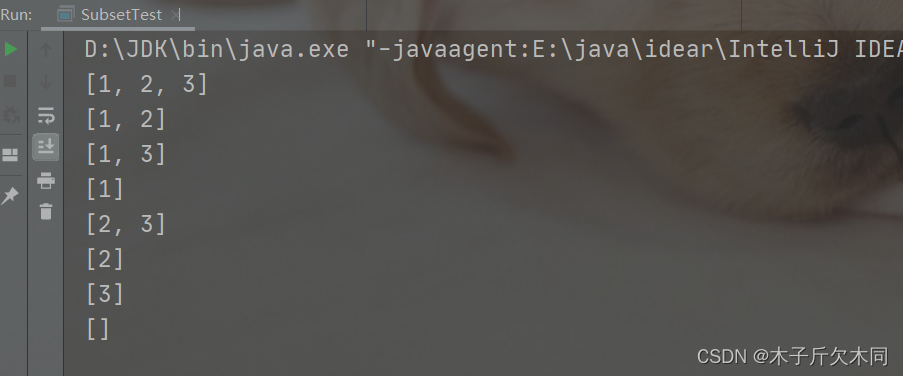
解法二

算法的策略相交于第一种解法有所不同，第一种解法是判断当前位置选不选的情况，所以决策树的叶子结点才是子集。

第二种解法是一棵多叉的决策树，是从一个子集的容量问题上来分情况，例如：子集里面的元素可以是0个、1个、2个，也可以是3个。具体如下所示：

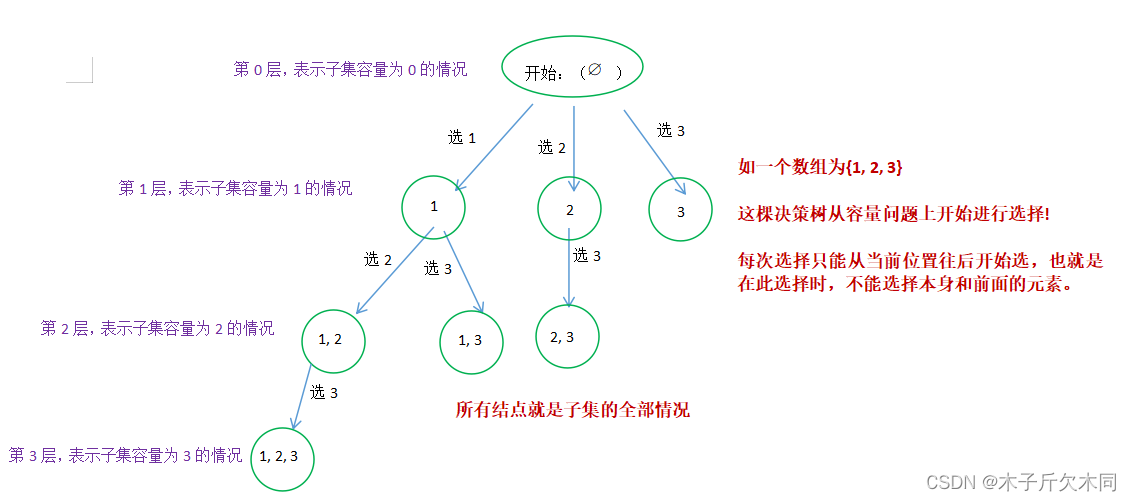
class Solution {

    List<Integer> path;//用来记录一次的子集
    List<List<Integer>> ret;//用来记录总的子集情况

    public List<List<Integer>> subsets(int[] nums) {
        //1.初始化
        path = new ArrayList<>();
        ret = new ArrayList<>();
        //2.回溯的核心
        dfs(nums, 0);
        return ret;
    }

    //nums：需要计算子集的数组
    //deep：表示当前来到树的第几层
    public void dfs(int nums[], int deep) {
        //因为每一个结点都是我需要的结果，所以每一个结点都要收集
        ret.add(new ArrayList<>(path));

        //回溯开始
        //这里必须从deep开始，表示在nums数组中的第几位开始
        //只有这样，才不会导致重复选取
        for (int i = deep; i < nums.length; i++) {
            path.add(nums[i]);
            dfs(nums, i + 1);
            //恢复现场
            path.remove(path.size() - 1);
        }
    }
}

解法三

解法三是在解法一的思路上，加上一个boolean数组来判断当前位置选没选，决策树如下：

public class Test10 {

    static int N = 3;
    static char[] a = {'a', 'b', 'c'};
    static boolean[] x = {false, false, false};

    public static void main(String[] args) {
        backTrack(0);
    }
//回溯的核心
    public static void backTrack(int level) {
        if (level == N) {
            output();
        } else {
            x[level] = false;//不选
            backTrack(level + 1);
            x[level] = true;
            backTrack(level + 1);
        }
    }
//打印数据
    public static void output() {
        System.out.print("{");
        for (int i = 0; i < x.length; i++) {
//如果这个位置是选的话，也就是x[i] == true，就选a[i]
            if (x[i]) {
                System.out.print(a[i] + " ");
            }
        }
        System.out.print("}");
        System.out.println();
    }
}

2. 0-1背包问题（使用子集树解决）

题目描述：
你有?个背包，最多能容纳的体积是V。
现在有 n 个物品，第 i 个物品的体积为vi，价值为wi。
（1）求这个背包?多能装多?价值的物品
（2）若背包恰好装满，求?多能装多?价值的物品

true表示选这物品，false表示不选这物品

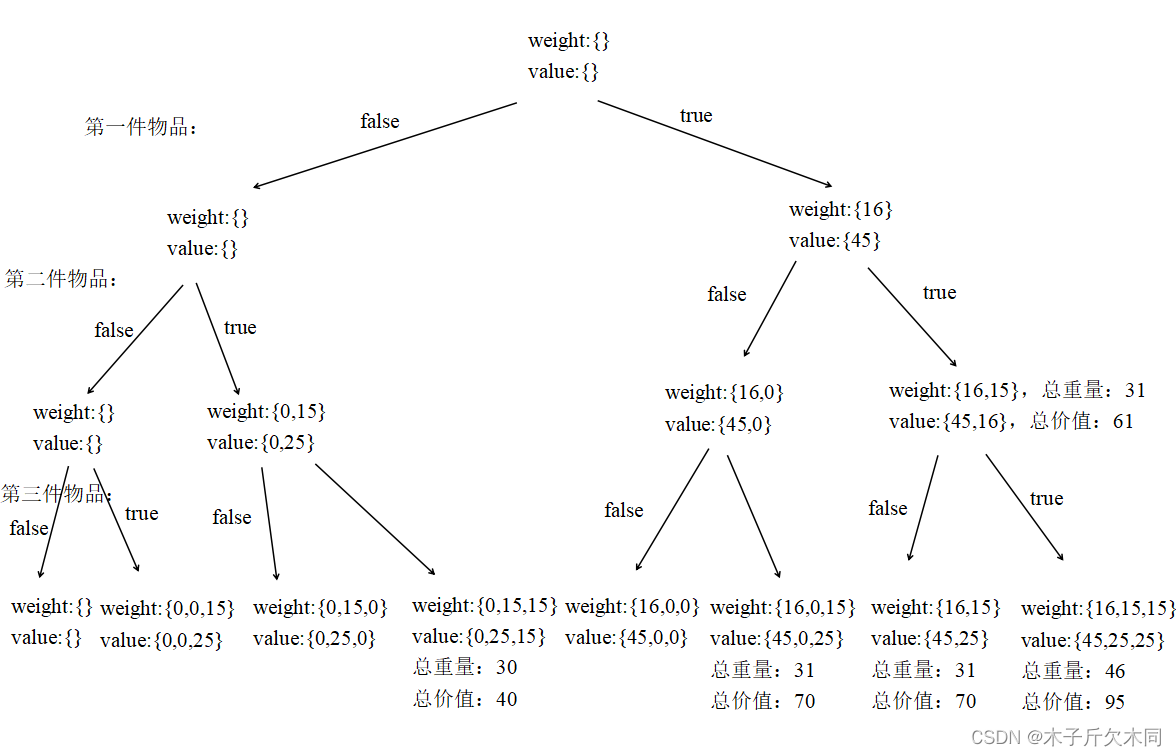
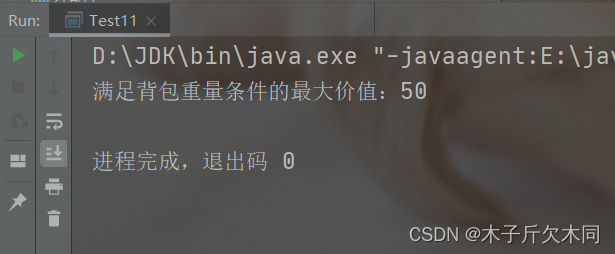
public class Test11 {
    static int C = 30;//背包容量
    static int N = 3;//三个物品
    static int weights[] = {16, 15, 15};//重量
    static int values[] = {45, 25, 25};//价值
    static boolean[] x = {false, false, false};//作为判断选不选的问题
    //保存最大价值
    static int maxValuse = 0;

    //回溯核心
    //w：当前背包所放物品重量和
    //v：当前背包所放物品价值和
    public static void backtrack(int level, int w, int v) {
        if (level == N) {
            output(v);
        } else {
            x[level] = false;//不选
            backtrack(level + 1, w, v);
            x[level] = true;//选
            if (legal(w + weights[level]))
                backtrack(level + 1, w + weights[level], v + values[level]);
        }
    }

    //判断当前背包重量是不是合法
    public static boolean legal(int w) {
        return w <= C;
    }

    //v：当前的价值
    public static void output(int v) {
        maxValuse = Math.max(v, maxValuse);
    }

    public static void main(String[] args) {
        backtrack(0, 0, 0);
        System.out.println(maxValuse);
    }
}

3.?最小重量机器设计问题

题目描述：设某一机器由 N 个部件组成，每一种部件都可以从 M 个不同的供应商处购得。设 W 是从供应商j处购得的部件i的重量, C 是相应的价格。 试设计一个算法，给出总价格不超过 D 的最小重量机器设计。

解决方案如下：

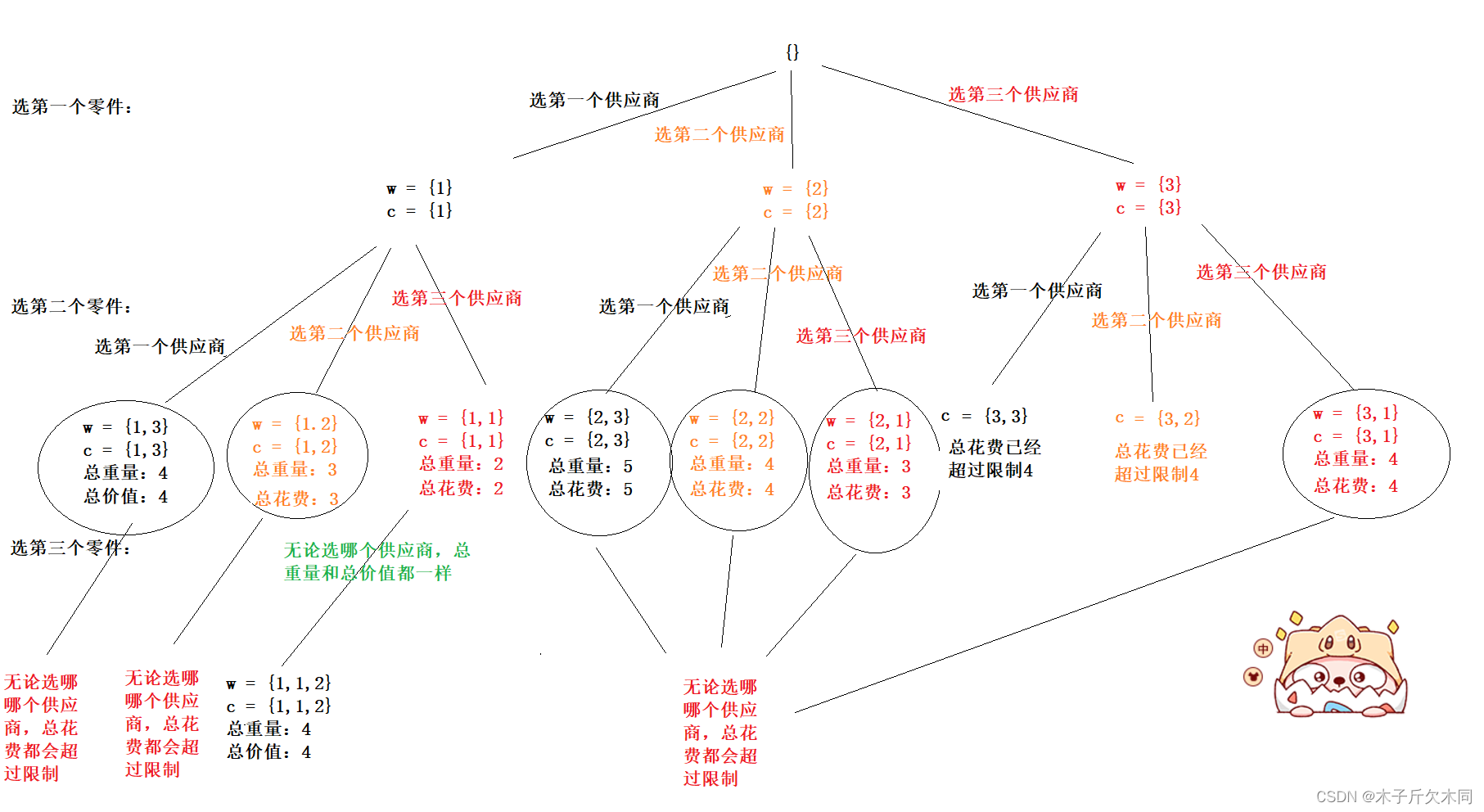
public class Test12 {
    static int N = 3;//部件数
    static int Suppliers = 3;//供应商数
    static int D = 4;//总价格限制
    static int minWeight = Integer.MAX_VALUE;//这个变量用来保存最小重量
    static int[][] weight = {{1, 2, 3}, {3, 2, 1}, {2, 1, 2}};//重量数组
    static int[][] value = {{1, 2, 3}, {3, 2, 1}, {2, 2, 2}};//价格数组
    static int[] str = new int[3];
    /*
    false表示选，true表示不选
     */
    //默认值是false
    //为什么是二维数组呢？因为要与w和v二维数组对应
    static boolean[][] flag = new boolean[3][3];

    //打印每个零件的供应商
    public static void output() {

        for (int i = 0; i < N; i++) {
            for (int j = 0; j < Suppliers; j++) {
                if (flag[i][j])
                    str[i] = j + 1;
            }

        }
    }

    /*
    w：表示当前的重量
    v：表示当前的价值
    level：表示层数；0表示选第一个零件、1表示选第二个零件、2表示选第三个零件
     */
    public static void backtrack(int level, int w, int v) {
        //能走到这个if肯定是没超过限制重量D
        if (level == N) {
            int tmp = minWeight;
            minWeight = Math.min(minWeight, w);
            if (tmp != minWeight) {
                output();
            }
        } else {
            //表示从第一个供应商开始选择
            for (int i = 0; i < Suppliers; i++) {
                flag[level][i] = true;
                if (D >= v + value[level][i]) {
                    backtrack(level + 1, w +
                            weight[level][i], v + value[level][i]);
                }
                //这个为什么要改为false呢？
                //方便output方法的实现，找到每个零件的供应商
                flag[level][i] = false;
            }
        }
    }

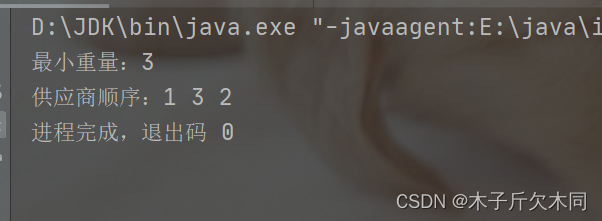
    public static void main(String[] args) {

        backtrack(0, 0, 0);
        System.out.println("最小重量：" + minWeight);
        System.out.print("供应商顺序：");
        for (int i = 0; i < str.length; i++) {
            System.out.print(str[i] + " ");
        }
    }

}