数据结构和算法-查找的基本概念和顺序查找与折半查找与分块查找

2023-12-19 05:31:28

文章目录

查找的基本概念

总览

在这里插入图片描述

基本概念

查找表就是要查找的那堆元素组成的
在这里插入图片描述
此时关键字是学号，因为没有重复的
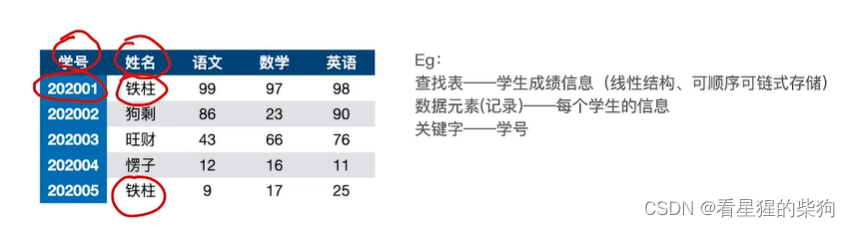
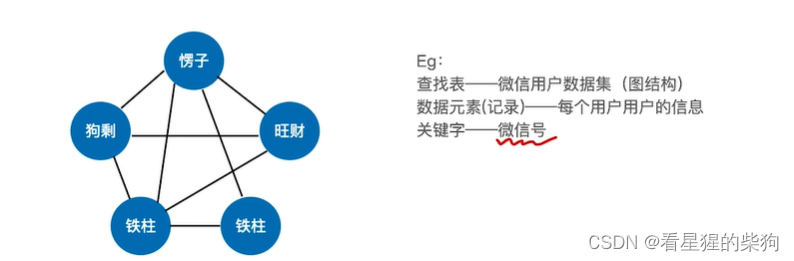
在这里插入图片描述
在这里插入图片描述

对查找表的常见操作

静态：查找表中 元素个数不会变化
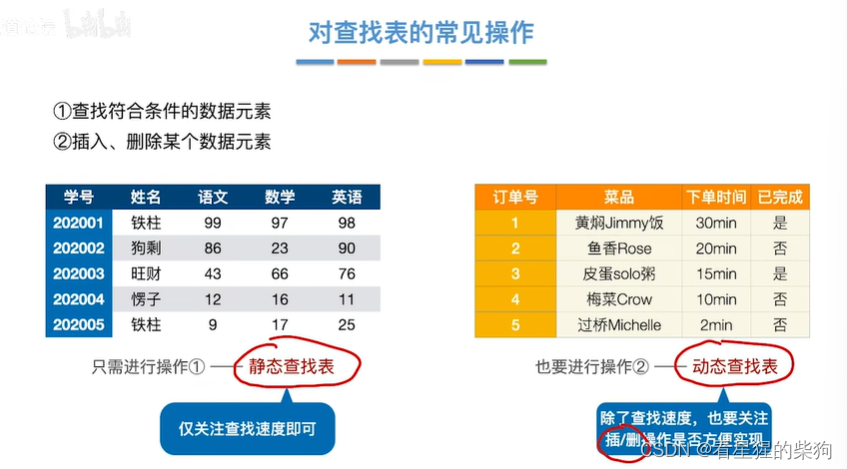
在这里插入图片描述

查找算法的评价指标

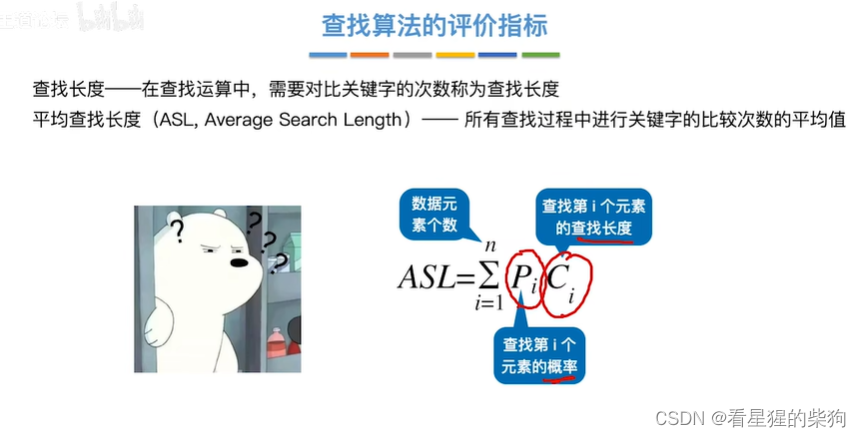
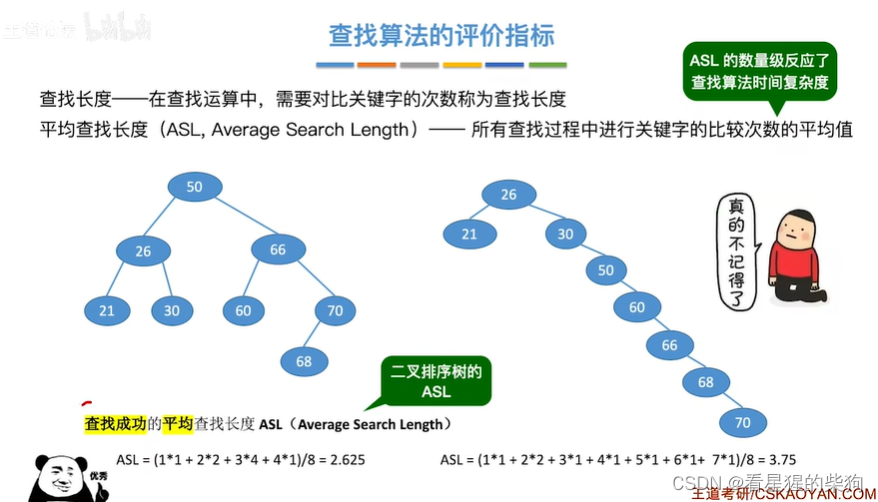
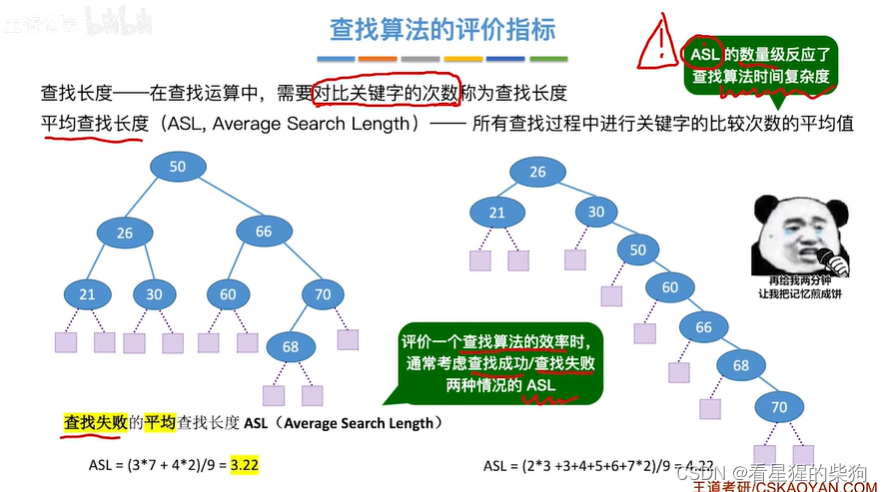
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

小结

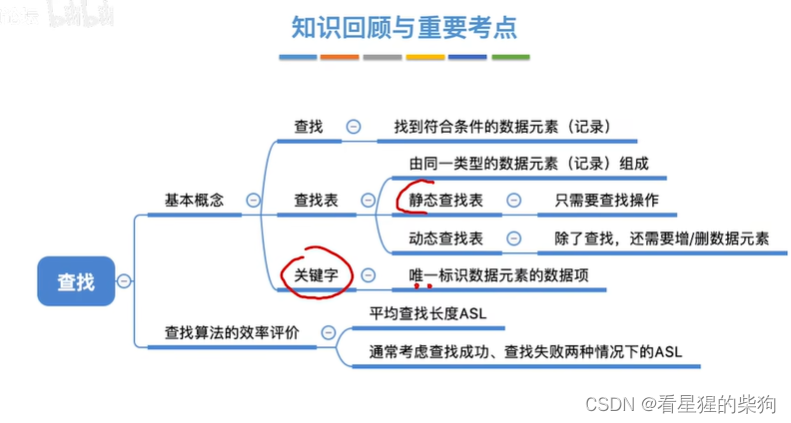
在这里插入图片描述

顺序查找

总览

在这里插入图片描述

顺序查找的算法思想

在这里插入图片描述

顺序查找的实现

当i等于表的总长度时，说明找遍了所有的都没有找到，所以此时返回-1，否则就是找到了，返回对应的索引i
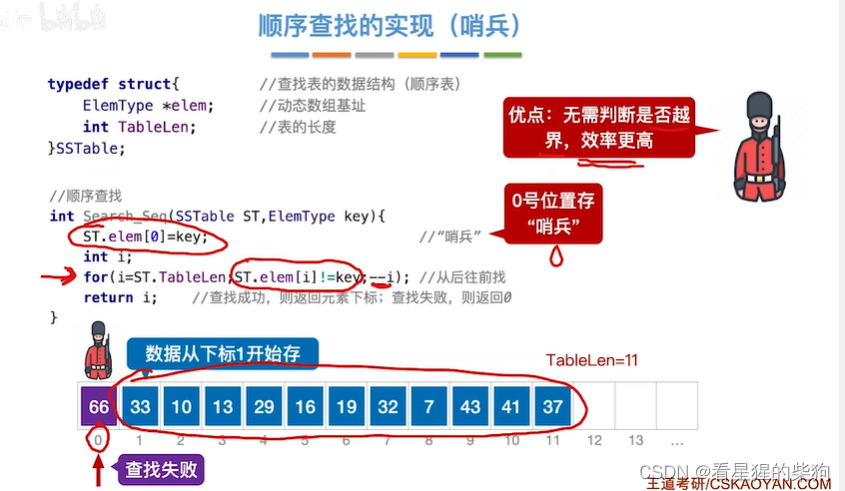
在这里插入图片描述

顺序查找的实现（哨兵）

当查找到零号元素时一定符合，此时返回i正好是0，也正好说明没有找到
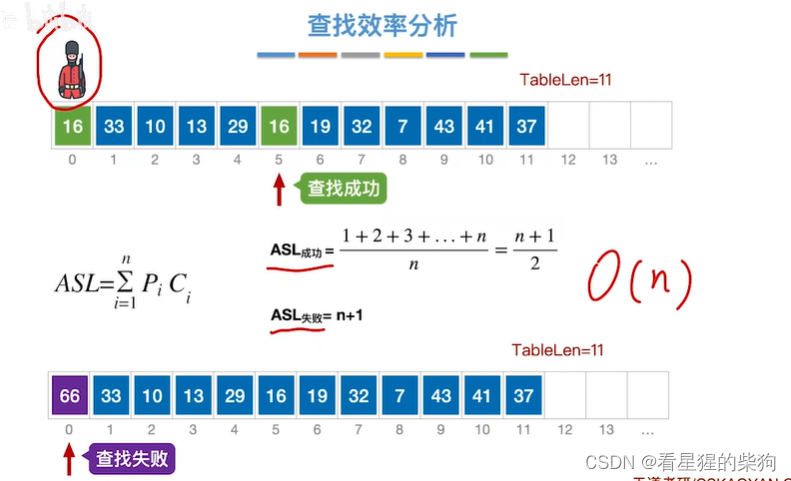
在这里插入图片描述

查找效率分析

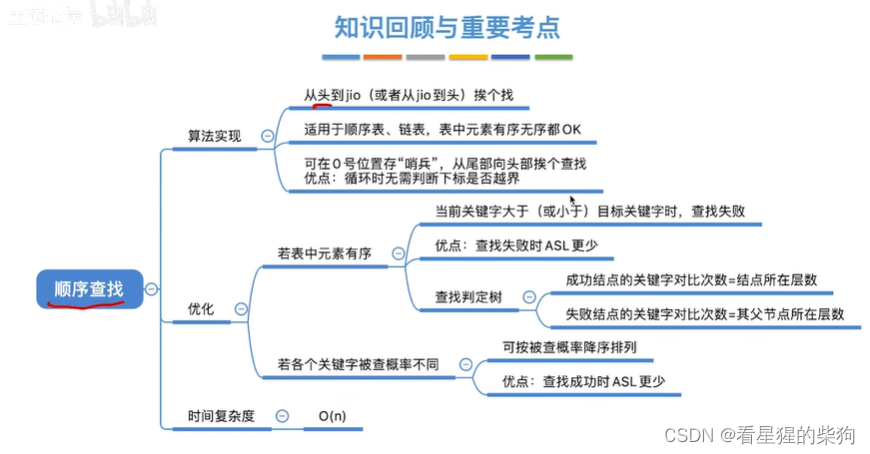
在这里插入图片描述

顺序查找的优化（有序表）

当查找目标小于当前遍历的元素时，意味着查找失败
ASL两个n是最后一个无论是小于还是大于都算查找失败

在这里插入图片描述

用查找判定树分析ASL

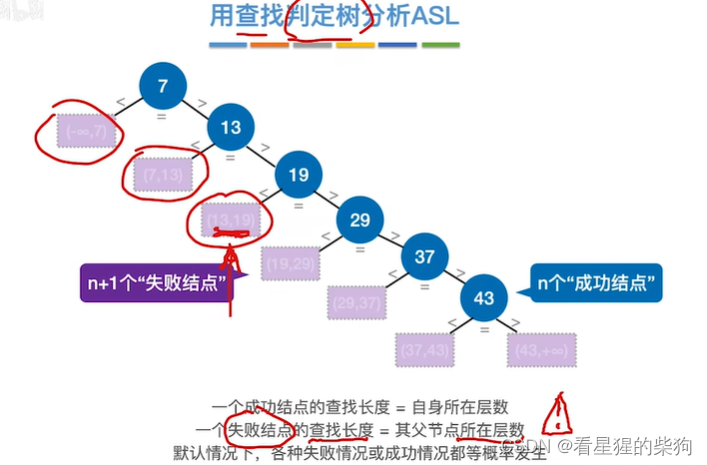
在这里插入图片描述

顺序查找的优化（被查概率不相等）

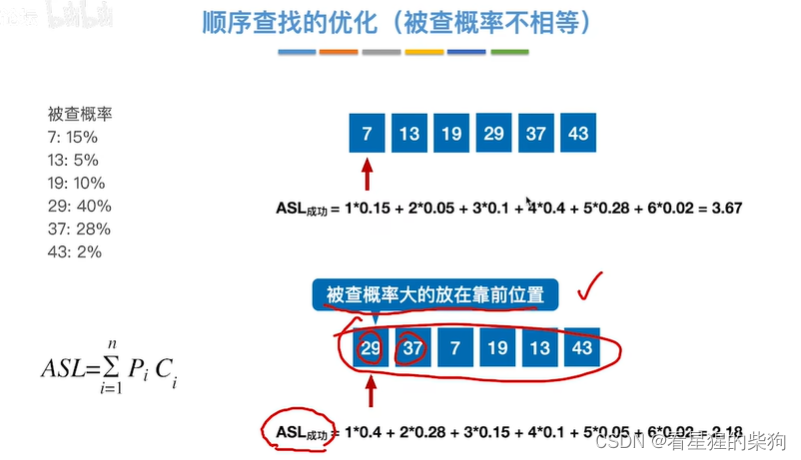
在这里插入图片描述

小结

在这里插入图片描述

折半查找

总览

在这里插入图片描述

折半查找的算法思想（二分查找）

查找成功

比较mid对应的数组元素中的值，此时要查找的值大于该值

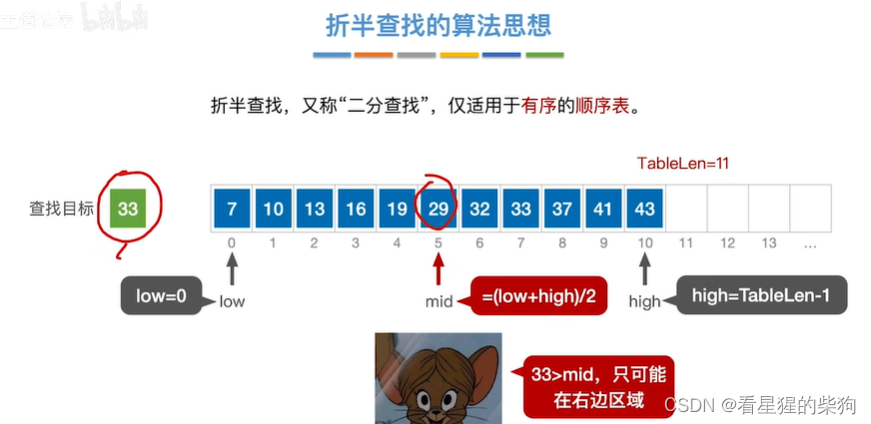
在这里插入图片描述
移动low为mid+1，更新mid，再次比较，此时要查找的值小于mid处对应的值
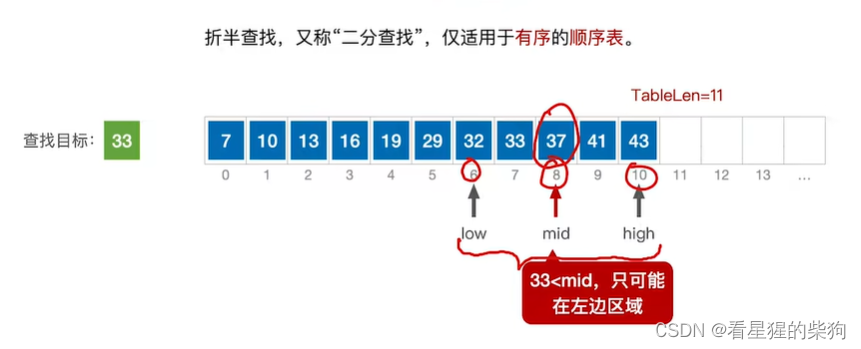
在这里插入图片描述

移动high为mid-1，计算mid，此时mid的值若为小数则向下取整，再次比较，此时查找目标大于mid对应的值
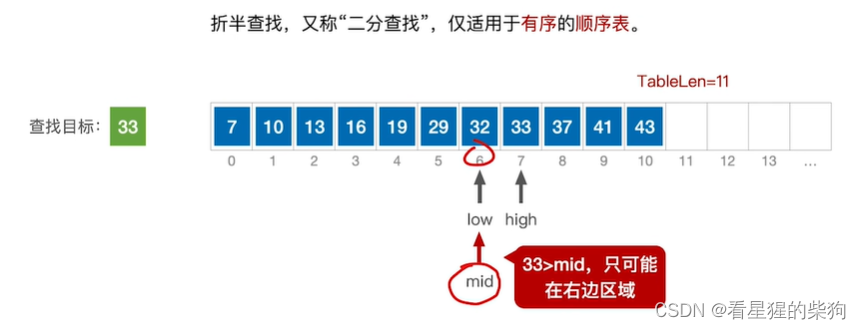
在这里插入图片描述
移动low为mid+1，计算mid，再次比较发现相等

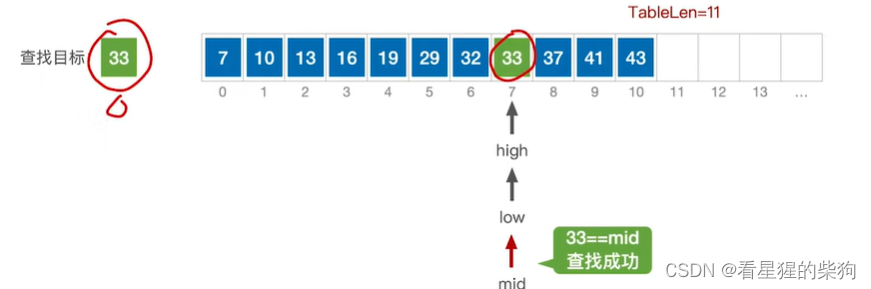
在这里插入图片描述

查找失败

计算mid，比较，发现小于

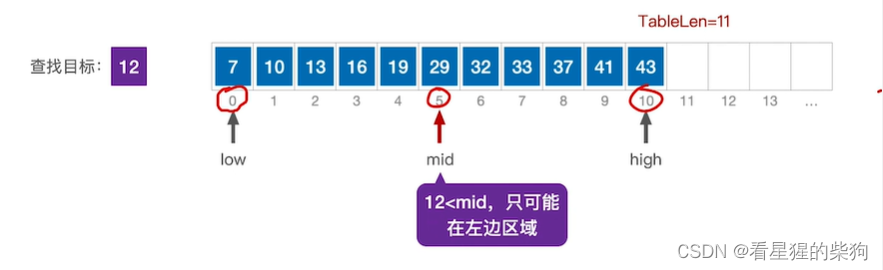
在这里插入图片描述
移动high为mid-1，计算mid，再次比较，发现小于
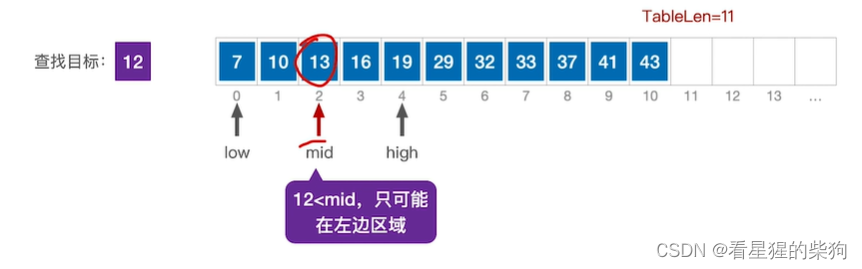
在这里插入图片描述
移动high为mid-1，再次计算mid，比较，发现大于
在这里插入图片描述
移动low为mid+1，计算mid，比较，此时大于
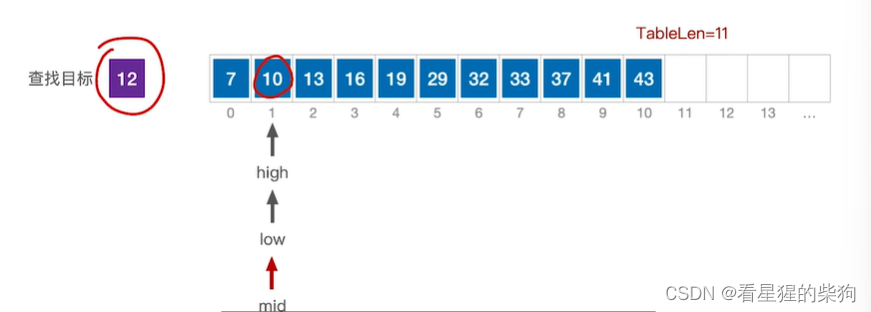
在这里插入图片描述
移动low为mid+1,low<high,查找失败

在这里插入图片描述

折半查找的实现

链表不具备随机存取的特性

每次循环对应low和high相比上一次不完全一样
在这里插入图片描述

查找效率分析

默认每种失败的情况相等
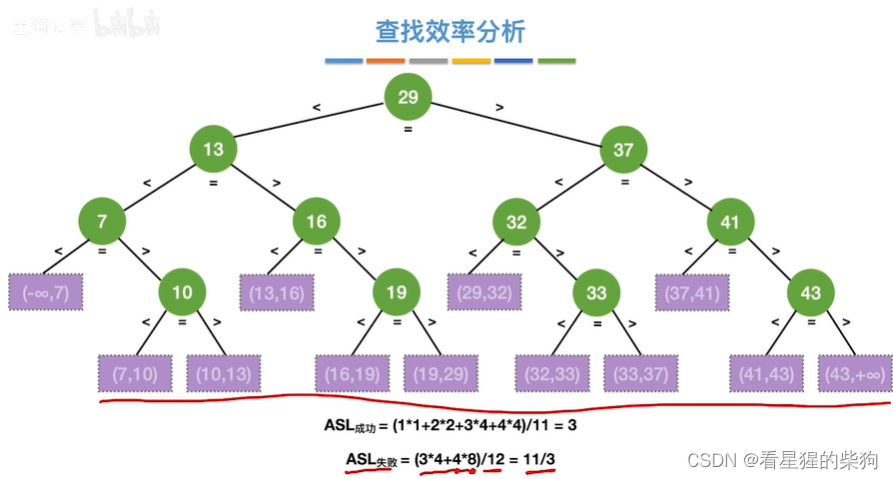
在这里插入图片描述

折半查找判定树的构造

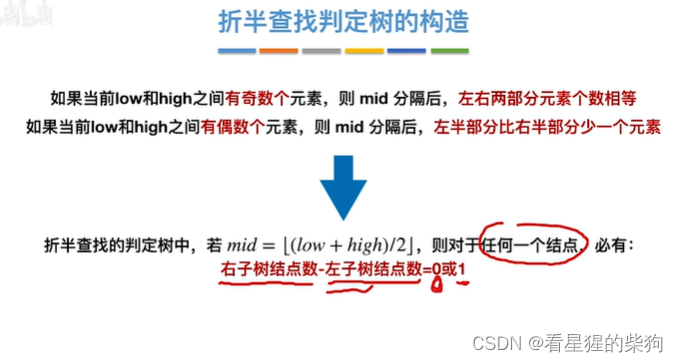
在这里插入图片描述
节点中的数字代表这是此时这是第几个元素对应查找表的位置
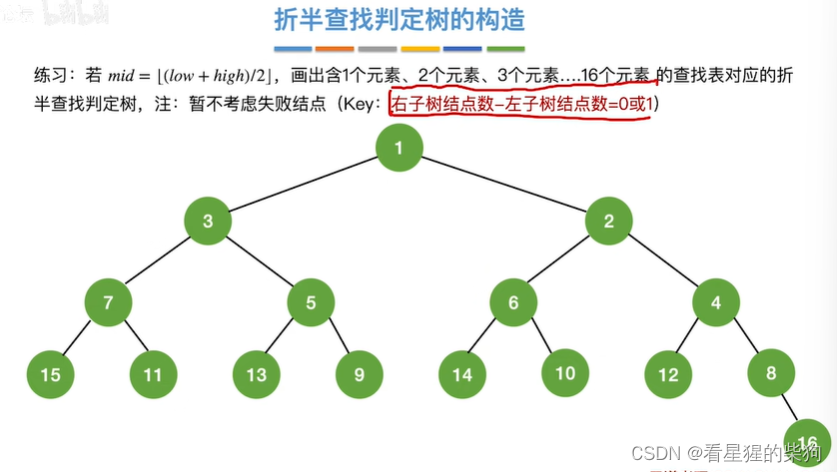
在这里插入图片描述
任何一个节点的左子树和右子树的深度之差都不会超过1
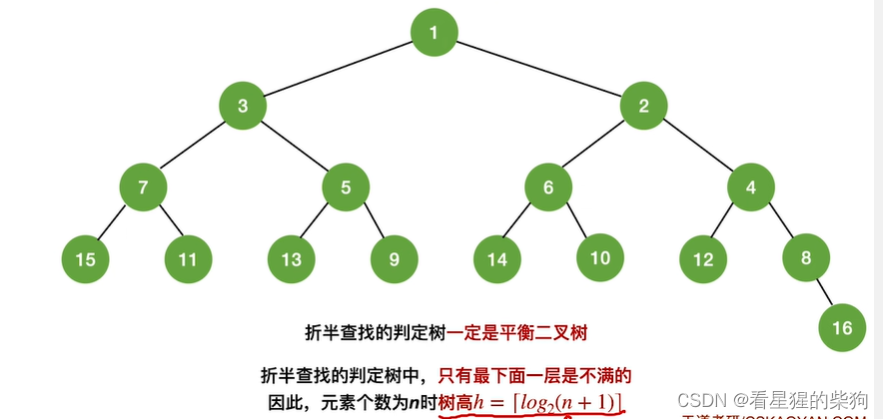
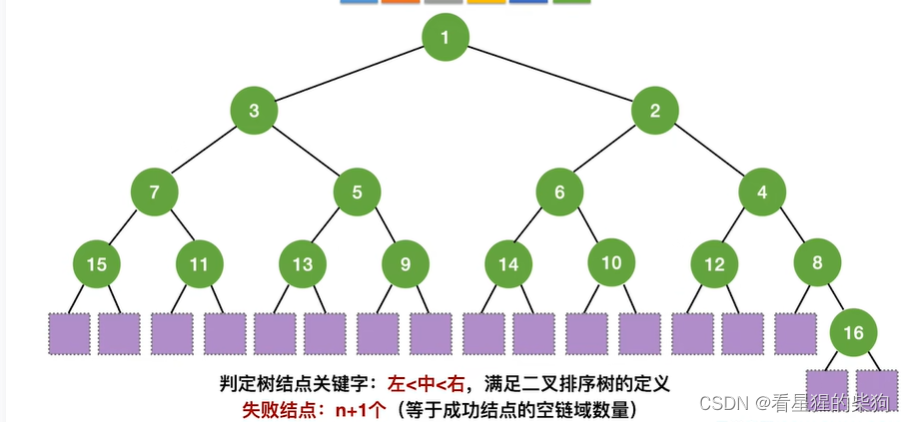
在这里插入图片描述
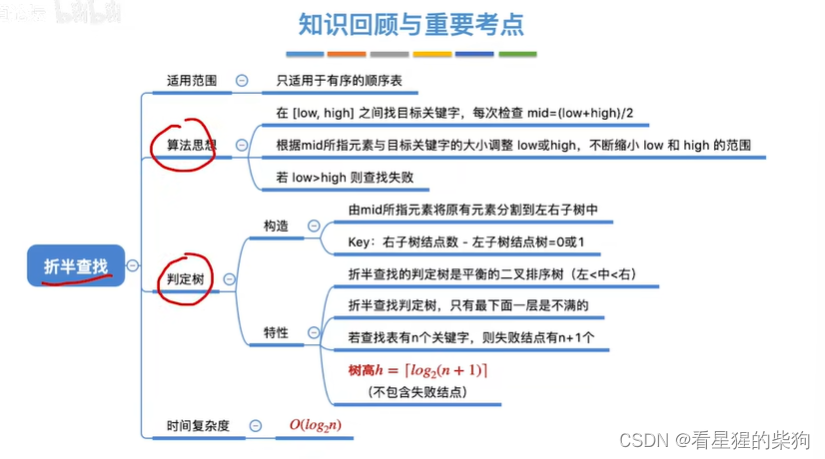
在这里插入图片描述

折半查找的效率

在这里插入图片描述

小结

在这里插入图片描述

拓展思考

大部分情况下折半查找的速度是比顺序查找的速度更快的
但不是说折半查找的速度一定被顺序查找更快
如下图此时顺序查找第一次即可找到，但折半查找需要多次
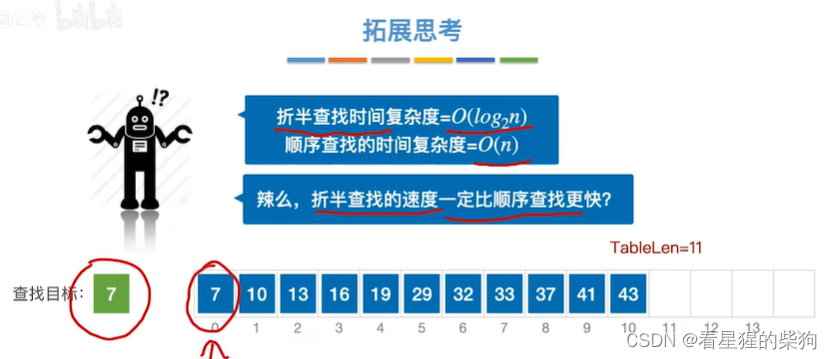
在这里插入图片描述
标号依然是第几个元素要出现的位置
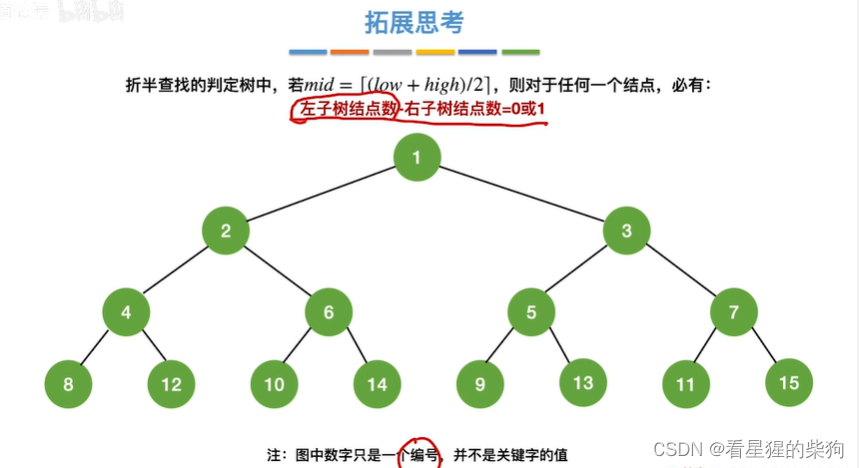
在这里插入图片描述

分块查找

总览

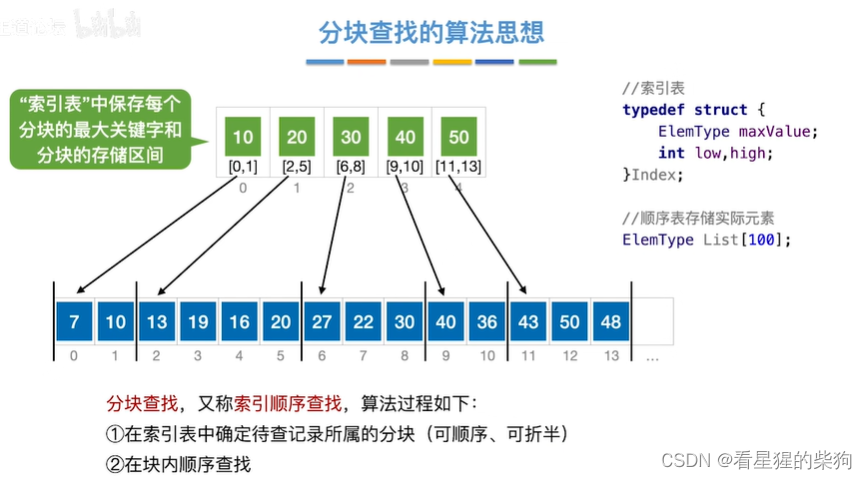
在这里插入图片描述

分块查找的算法思想

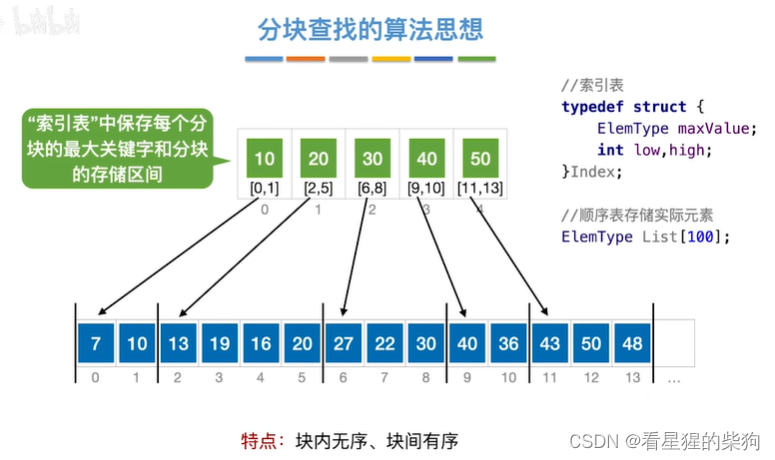
在这里插入图片描述
将查找目标和索引表中的值作比较，如果小于则可能在该表中的元素所对应的那块区间中，然后再到该区间去挨个比较查找
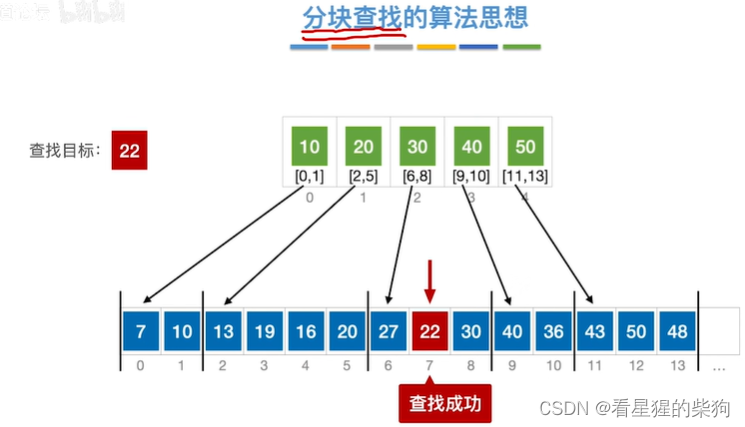
在这里插入图片描述
当超出该块对应区间范围时，查找失败

在这里插入图片描述

用折半查找索引

索引表是顺序的。可以用折半去查找对应的索引元素
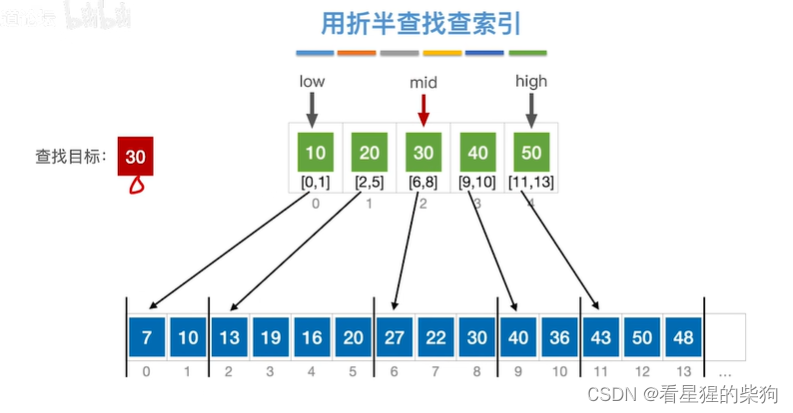
在这里插入图片描述
此时mid对应的大于查找目标，high移为mid-1
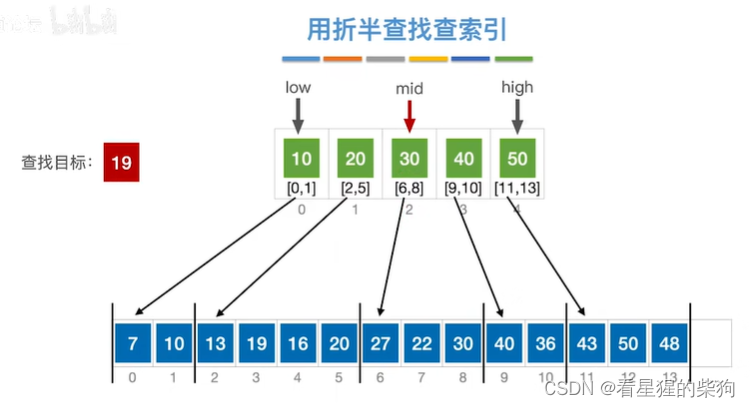
在这里插入图片描述
计算mid，此时mid小于查找目标，low移动为mid+1
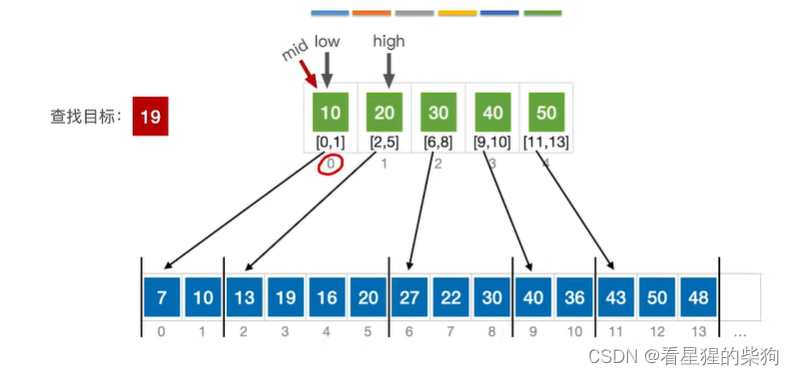
在这里插入图片描述
再次计算为mid，发现大于查找目标，high移为mid-1
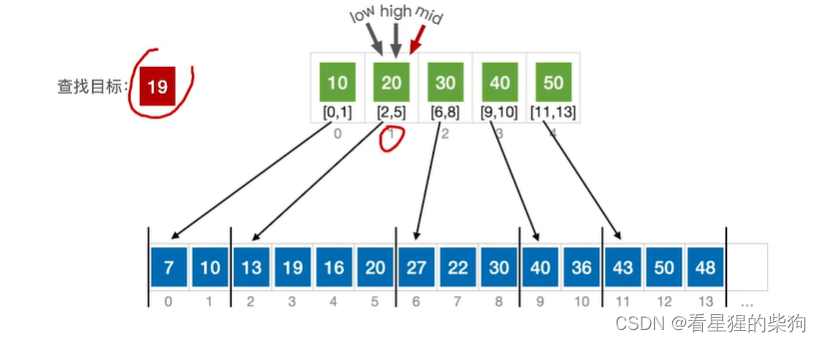
在这里插入图片描述
此时high小于low
（当low大于high时，要不就是high=mid-1,要不就是low=mid+1，但此时low对应的都是刚好大于查找元素的）

关于high右边一定大于查找目标，low左边一定小于查找目标。这是因为之前mid和low与high的转换机制决定的，因为low的左边都是小于等于原来的mid，而原来的mid又是小于查找目标的。high同理

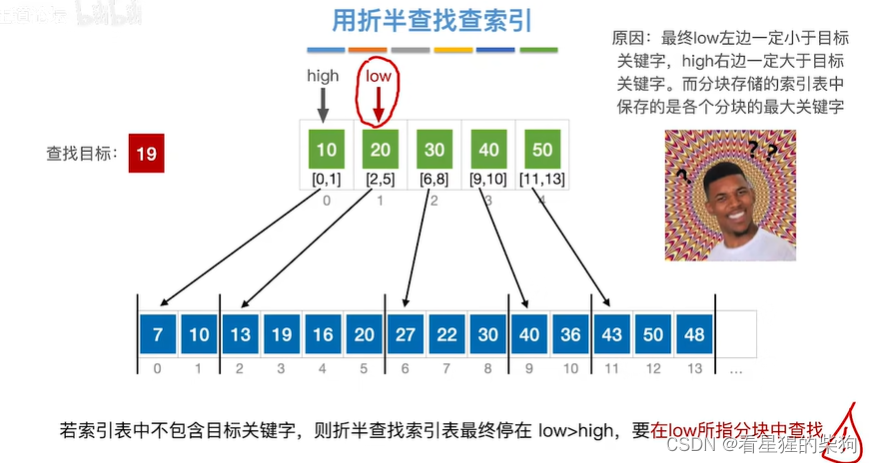
在这里插入图片描述
查找失败时是low超出索引了

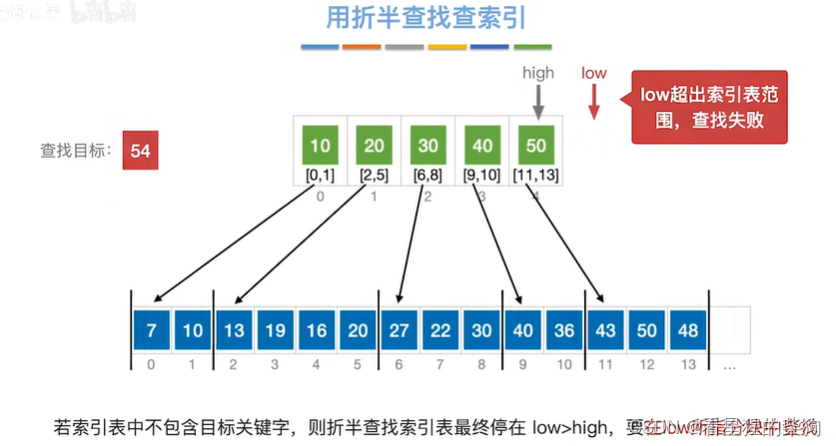
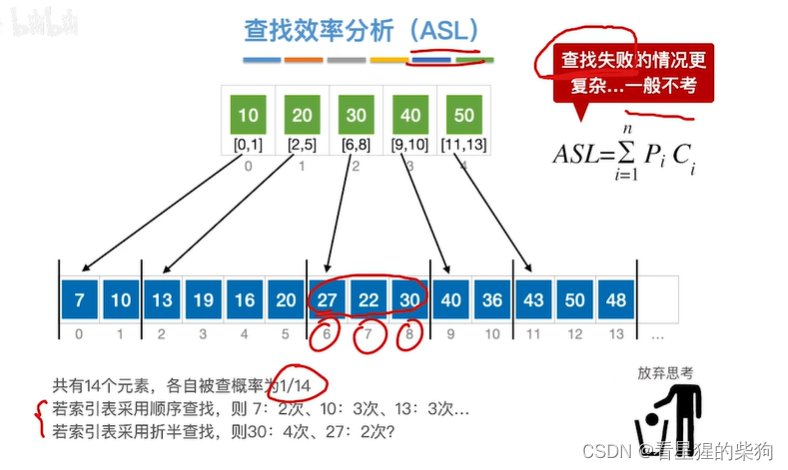
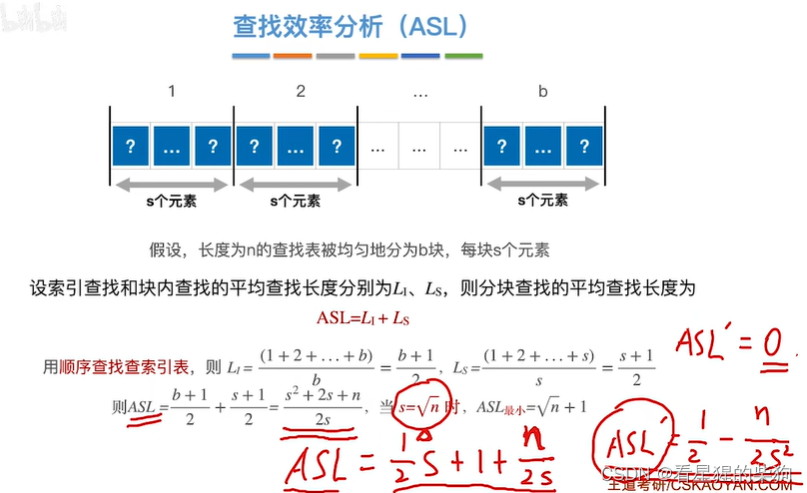
在这里插入图片描述

查找效率分析

查找27时，光折半查找就不止两次，与查找30时对应的折半查找根本不一样
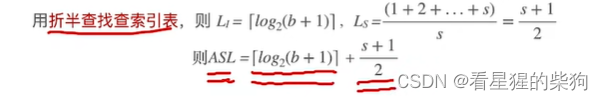
在这里插入图片描述
n=sb
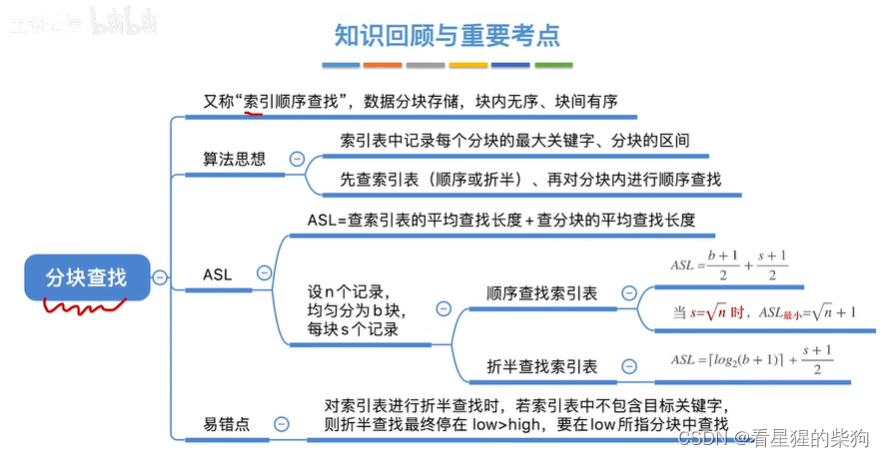
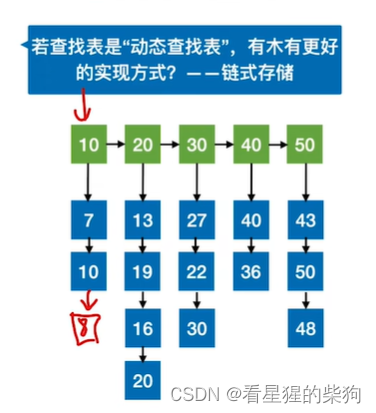
在这里插入图片描述
在这里插入图片描述

小结

在这里插入图片描述

拓展思考

查找表是顺序表时加入元素和删除元素非常麻烦
在这里插入图片描述

文章来源:https://blog.csdn.net/llovewuzhengzi/article/details/135055542
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。