Unity中URP下统一不同平台下的z值

2024-01-03 14:20:41

文章目录

前言

在之前的文章中，我们实现了URP下的雾效。

我们在这篇文章中，看一下Unity在URP下，计算雾效因子时是怎么统一Z值的。

一、ComputeFogFactor 来计算雾效混合因子

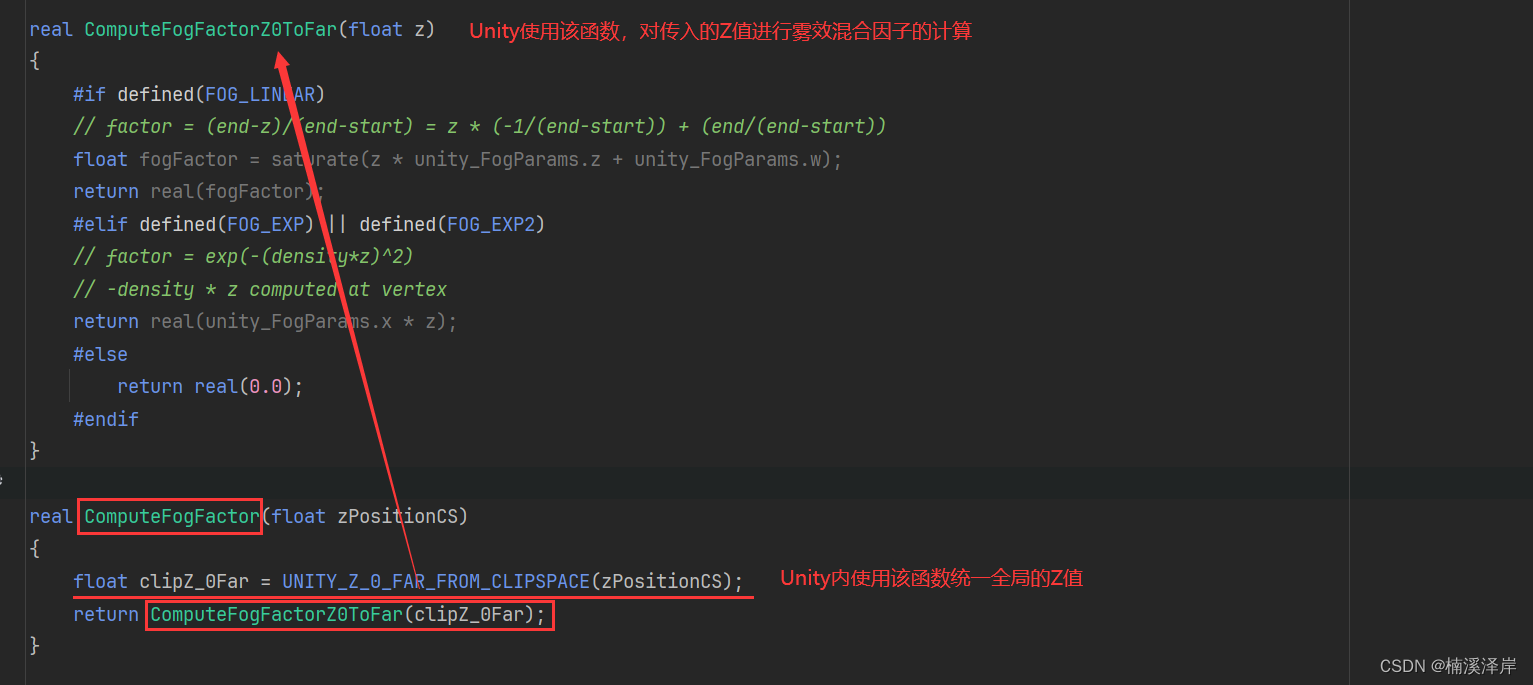
在这里插入图片描述

二、UNITY_Z_0_FAR_FROM_CLIPSPACE 来统一计算不同平台下的Z值

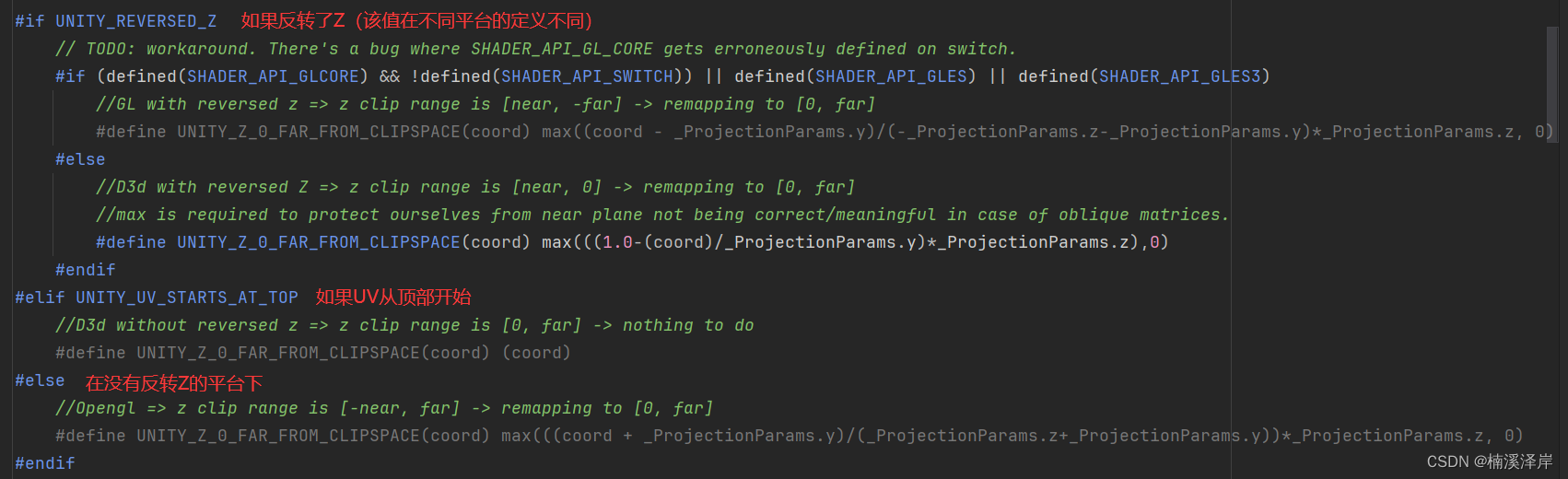
在这里插入图片描述

  • UNITY_REVERSED_Z(DX类平台都为1，其他平台都为0)
  • UNITY_UV_STARTS_AT_TOP(DX类平台都为1，其他平台都为0)
    （这个的作用应该是防止出现什么奇怪的平台时，对传入的Z值不做处理）

1、DirectX平台

  • 我们看一下反转过Z值的类DirectX平台，在处理雾效因子时，Z值是怎么处理的。
  • [near, 0] -> remapping to [0, far]

//D3d with reversed Z => z clip range is [near, 0] -> remapping to [0, far]
//max is required to protect ourselves from near plane not being correct/meaningful in case of oblique matrices.
#define UNITY_Z_0_FAR_FROM_CLIPSPACE(coord) max(((1.0-(coord)/_ProjectionParams.y)*_ProjectionParams.z),0)

n ≤ z ≤ 0 n \leq z \leq0 n≤z≤0

n ? n ≤ z ? n ≤ 0 ? n n - n \leq z - n\leq0 - n n?n≤z?n≤0?n

0 ≤ z ? n ≤ ? n 0 \leq z - n\leq- n 0≤z?n≤?n

0 ≤ ( z ? n ) 1 ? n ≤ ? n 1 ? n 0 \leq (z - n)\frac{1}{-n}\leq- n\frac{1}{-n} 0≤(z?n)?n1?≤?n?n1?

0 ≤ z ? n ? n ≤ 1 0 \leq \frac{z - n}{-n}\leq1 0≤?nz?n?≤1

0 ≤ z ? n ? n f ≤ f 0 \leq \frac{z - n}{-n}f\leq f 0≤?nz?n?f≤f

0 ≤ n ? z n f ≤ f 0 \leq \frac{n - z}{n}f\leq f 0≤nn?z?f≤f

0 ≤ ( n n ? x n ) f ≤ f 0 \leq (\frac{n}{n}-\frac{x}{n})f\leq f 0≤(nn??nx?)f≤f

0 ≤ ( 1 ? x n ) f ≤ f 0 \leq (1-\frac{x}{n})f\leq f 0≤(1?nx?)f≤f

  • 最后得出的公式是和我们Unity中使用的公式是一致的
    0 ≤ ( 1 ? x n ) f ≤ f 0 \leq (1-\frac{x}{n})f\leq f 0≤(1?nx?)f≤f

max(((1.0-(coord)/_ProjectionParams.y)*_ProjectionParams.z),0)

  • _ProjectionParams在Unity中的定义
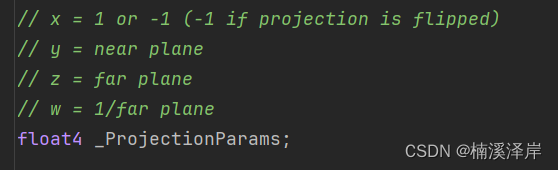
    在这里插入图片描述

2、GL平台下（在Unity.2022.LTS下，该功能没有完善)

  • 在GL平台下，我们也需要对Z值进行重映射
  • [near, -far] -> remapping to [0, far]

//GL with reversed z => z clip range is [near, -far] -> remapping to [0, far]
#define UNITY_Z_0_FAR_FROM_CLIPSPACE(coord) max((coord - _ProjectionParams.y)/(-_ProjectionParams.z-_ProjectionParams.y)*_ProjectionParams.z, 0)

n ≤ z ≤ ? f n \leq z \leq-f n≤z≤?f

n ? n ≤ z ? n ≤ ? f ? n n -n\leq z -n \leq-f - n n?n≤z?n≤?f?n

0 ≤ z ? n ≤ ? f ? n 0\leq z -n \leq-f - n 0≤z?n≤?f?n

0 ≤ ( z ? n ) 1 ? f ? n ≤ ? ( f + n ) 1 ? f ? n 0\leq (z -n) \frac{1}{-f-n}\leq-(f + n)\frac{1}{-f-n} 0≤(z?n)?f?n1?≤?(f+n)?f?n1?

0 ≤ z ? n ? f ? n ≤ 1 0\leq \frac{z-n}{-f-n}\leq1 0≤?f?nz?n?≤1

0 ≤ z ? n ? f ? n f ≤ f 0\leq \frac{z-n}{-f-n}f\leq f 0≤?f?nz?n?f≤f

  • 最后得出的公式是和我们Unity中使用的公式是一致的
    0 ≤ z ? n ? f ? n f ≤ f 0\leq \frac{z-n}{-f-n}f\leq f 0≤?f?nz?n?f≤f

max((coord - _ProjectionParams.y)/(-_ProjectionParams.z-_ProjectionParams.y)*_ProjectionParams.z, 0)

3、Opengl下

  • 在OpenGL平台下，我们
  • [-near, far] -> remapping to [0, far]

//Opengl => z clip range is [-near, far] -> remapping to [0, far]
#define UNITY_Z_0_FAR_FROM_CLIPSPACE(coord) max(((coord + _ProjectionParams.y)/(_ProjectionParams.z+_ProjectionParams.y))*_ProjectionParams.z, 0)

? n ≤ z ≤ f -n \leq z \leq f ?n≤z≤f

? n + n ≤ z + n ≤ f + n -n +n \leq z+n \leq f+n ?n+n≤z+n≤f+n

0 ≤ z + n ≤ f + n 0\leq z+n \leq f+n 0≤z+n≤f+n

0 ≤ z + n 1 f + n ≤ ( f + n ) 1 f + n 0\leq z+n\frac{1}{f+n}\leq (f+n)\frac{1}{f+n} 0≤z+nf+n1?≤(f+n)f+n1?

0 ≤ ( z + n ) 1 f + n ≤ 1 0\leq (z+n)\frac{1}{f+n}\leq 1 0≤(z+n)f+n1?≤1

0 ≤ ( z + n ) 1 f + n f ≤ f 0\leq (z+n)\frac{1}{f+n}f\leq f 0≤(z+n)f+n1?f≤f

  • 最后得出的公式是和我们Unity中使用的公式是一致的
    0 ≤ ( z + n ) 1 f + n f ≤ f 0\leq (z+n)\frac{1}{f+n}f\leq f 0≤(z+n)f+n1?f≤f

max(((coord + _ProjectionParams.y)/(_ProjectionParams.z+_ProjectionParams.y))*_ProjectionParams.z, 0)

文章来源:https://blog.csdn.net/qq_51603875/article/details/135342154
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。