堆排序算法
2023-12-28 20:40:53
堆排序是利用堆这种数据结构而设计的一种排序算法,堆具有以下特点:
1.完全二叉树
2.二叉树每个结点的值都大于或等于其左右结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右子结点的值,称为小顶堆
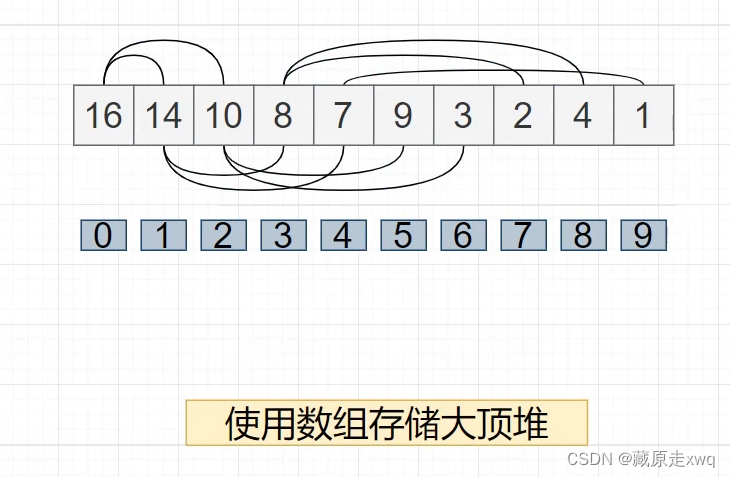
大顶堆
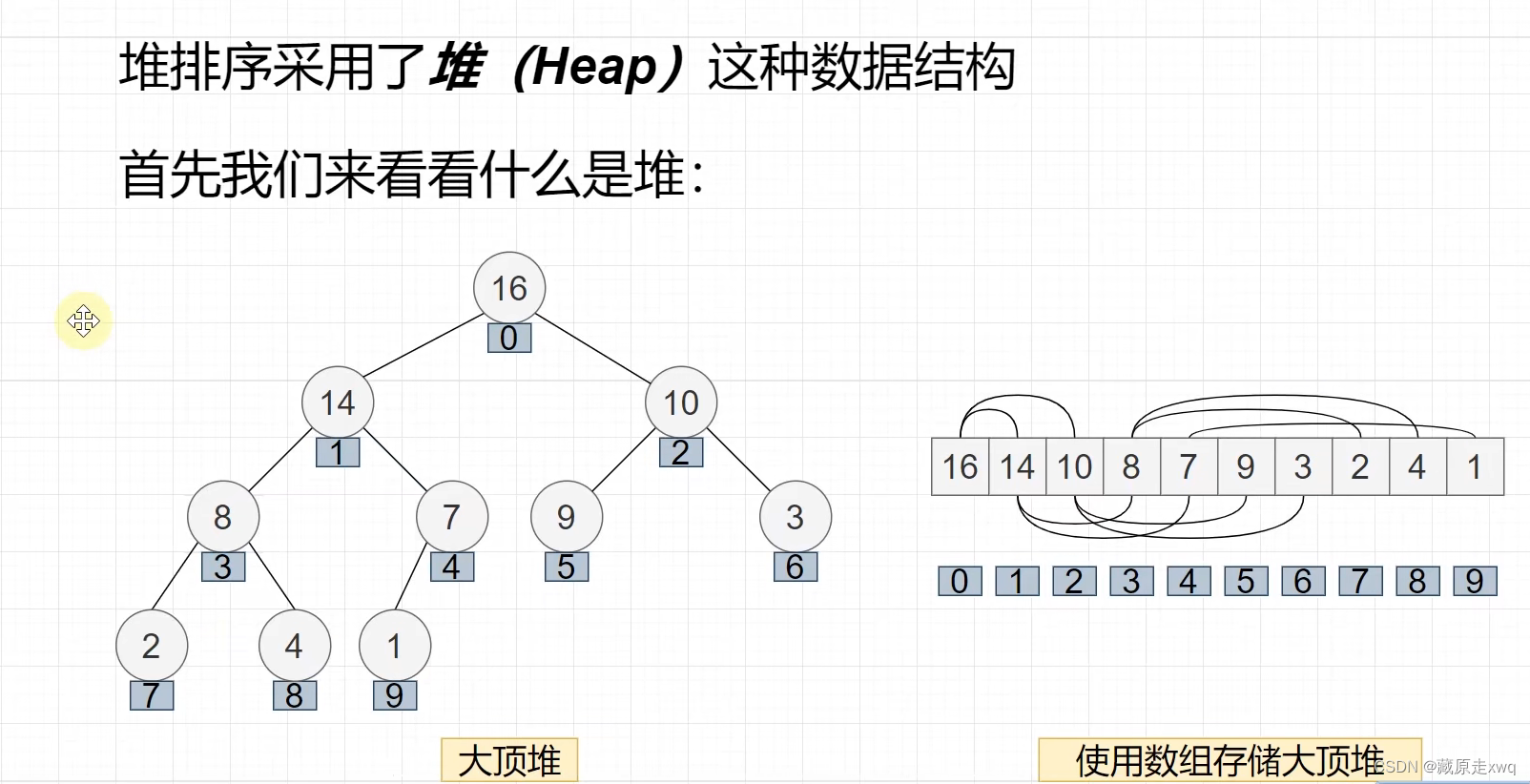
大顶堆:所有节点左孩子与右孩子都小于父节点,则满足大顶堆规律
注意:堆要按照完全二叉树的排法依次排列树
大顶堆数组下标规律:

小顶堆

小顶堆:所有节点左孩子与右孩子都大于父节点,则满足小顶堆规律
维护顶堆的性质
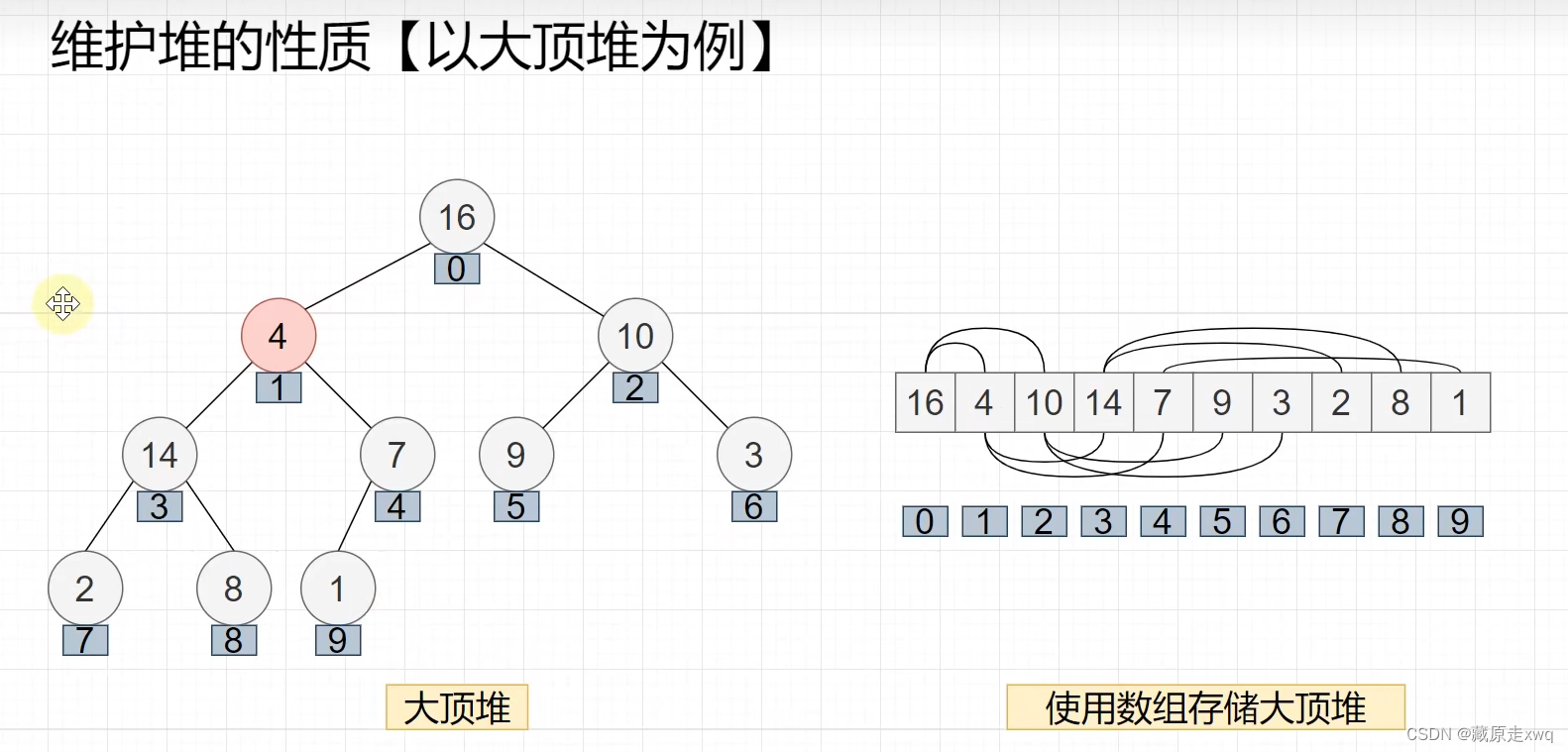
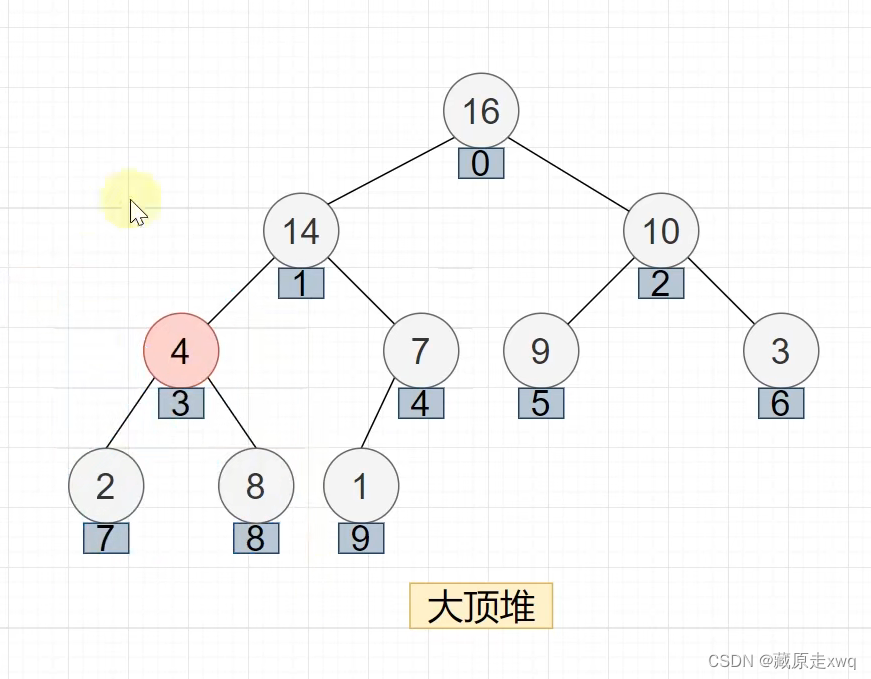
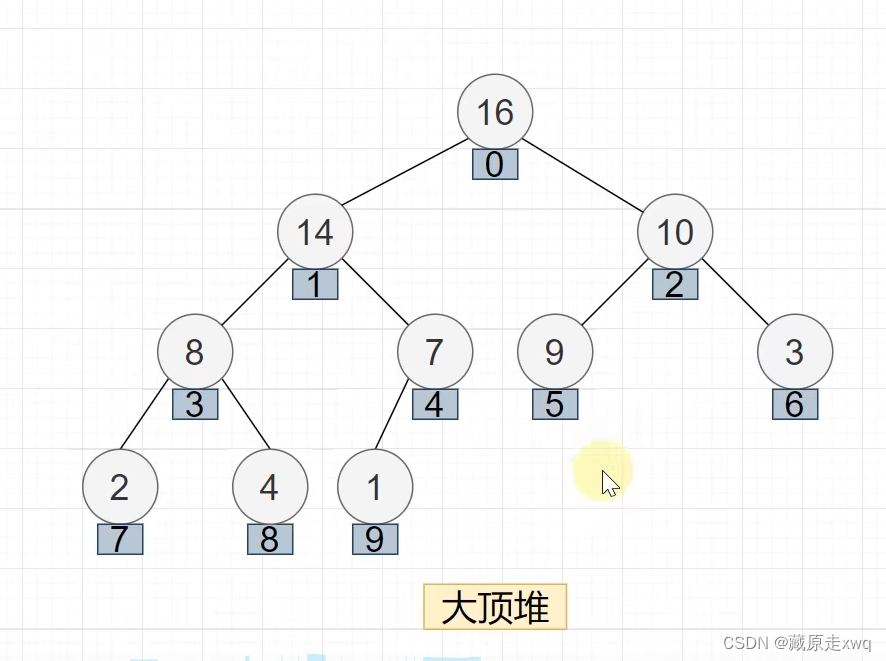
代码实现:
//维护堆的性质
//arr 存储堆的数组
//n 数组长度
// 带维护节点的下标
void heapify(int arr[], int n, int i) {
int largest = i;
int lson = i * 2 + 1;
int rson = i * 2 + 2;
if (lson < n && arr[largest] < arr[lson])
largest = lson;
if (rson < n && arr[largest] < arr[rson])
largest = rson;
if (largest != i)
{
swap(&arr[largest], &arr[i]);
heapify(arr, n, largest);
}
}最终代码实现:?
//维护堆的性质
//arr 存储堆的数组
//n 数组长度
// 带维护节点的下标
#include <stdio.h>
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
void heapify(int arr[], int len, int i)
{
int largest = i;
int lson = i * 2 + 1;
int rson = i * 2 + 2;
if (lson < len && arr[largest] < arr[lson])
largest = lson;
if (rson < len && arr[largest] < arr[rson])
largest = rson;
if (largest != i)
{
swap(&arr[largest], &arr[i]);
heapify(arr, len, largest);
}
}
void heap_sort(int arr[], int len)
{
int i;
// 建堆
for (i = len/2-1; i >= 0; i--)//i = len/2-1表示从最后一个父结点开始,最后一个结点下标为
heapify(arr, len, i); //len-1,由前面的数组下标规律得下标为i的结点的父结点为
//(i-1)/2,所以最后一个父结点下标为(len-1-1)/2
//所以就是len/2-1
// 排序
for (i = len - 1; i > 0; i--)
{
swap(&arr[i], &arr[0]);
heapify(arr, i, 0);
}
}
int main()
{
int arr[1000];
int n = 0;
// 输入数组大小
scanf("%d", &n);
// 输入数组元素
for (int i = 0; i < n; i++)
{
scanf("%d", &arr[i]);
}
// 执行堆排序
heap_sort(arr, n);
// 输出排序后的数组
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
return 0;
}
文章来源:https://blog.csdn.net/2303_80475208/article/details/135276086
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!