数据结构——栈（Stack）

目录

1.栈的介绍

2.栈工程

2.1 栈的定义

2.1.1 单链表实现栈

2.1.2 数组实现栈

2.1.2.1 静态数组栈

2.1.2.2 动态数组栈

2.2?栈的函数接口

2.2.1 栈的初始化

2.2.2 栈的数据插入（入栈）

2.2.3 栈的数据删除（出栈）

2.2.4 判断栈是否为空

2.2.5 取栈顶数据

2.2.6 栈数据统计

2.2.7 栈销毁

3. 栈总结反思

---

1.栈的介绍

? ? ? ? 栈这个东西我们并不陌生，有过一些基础知识的同志都知道，在存储器映像中就有一块存储区域被称为栈。这个栈主要是存储非静态局部变量，函数调用所开辟出的栈帧也在这块区域。对于这块区域，我们很明确的一点就是它的特征：先进后出，后进先出。在程序运行时（以Linux+IA32为例），栈顶指针esp在面对push和pop指令时会对应的减或加，栈空间的开辟和释放都是由esp指针来标定的。所以可以看到在栈区内，当要完成空间释放或申请时，总是在对最顶部的空间进行操作，即满足“先进后出，后进先出”的规则。

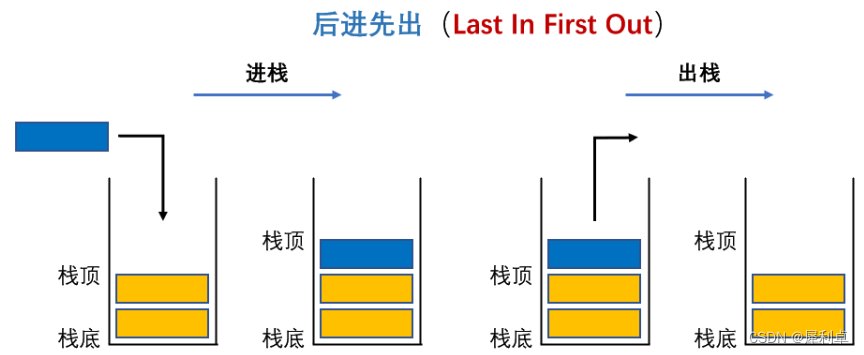
? ? ? ? 我们今天要介绍的栈则是一种数据结构，也属于线性表的一种，其重要特征就是我们刚才所提到的先进后出，后进先出。当数据存入时，会采取push（入栈/压栈）操作，将数据存储在栈顶；当数据删除时，会采取pop（出栈/弹栈）操作，将位于栈顶位置的数据删除。

2.栈工程

2.1 栈的定义

? ? ? ? 在实现栈的时候，我们需要考虑数据存储的方式。我们到目前掌握的存储方式有如顺序表的数组的结构，除此之外，还有链表结构。在实现栈这一方面，链表和数组的方式存储都可以。但是考虑到我们在需要频繁地访问栈顶，我们需要对这两种方式有所规定。

2.1.1 单链表实现栈

? ? ? ? 使用单链表的时候我们要规定好栈顶和栈底。因为对于栈这种数据结构，我们需要频繁地访问栈顶，但是对于单链表而言其数据的插入是将结点链接在链表末端。两相对比，我们发现使用单链表在入栈出栈的时候代价很大，需要遍历链表。所以我们一般不使用单链表来实现栈。

2.1.2 数组实现栈

? ? ? ? 使用数组实现栈也同样需要先明确栈顶栈底的位置。因为栈顶是“灵活多变”的，栈顶会随着数据的插入和删除而更改位置。对于一个数组而言很明显下标大的一端更容易适应这样的特性，所以我们一般将下标为0的一端作为栈底，将下标较大的一端作为栈顶。

? ? ? ? 在明确了数组的格式后，我们自然的想到动态的数组和静态的数组两种结构。

2.1.2.1 静态数组栈

? ? ? ? 对于一个静态数组栈，其数组长度是定长的，我们定义一个常量来统一管理。其栈结构（结构体）中除了一个存储数据的定长数组之外，还应该有一个成员来标识栈顶的位置，便于我们对栈进行访问。

//静态
typedef int STDataType;
#define N 10
typedef struct Stack
{
 STDataType _a[N];
 int _top; // 栈顶
}Stack;

2.1.2.2 动态数组栈

? ? ? ? 对于动态数组的栈来说，为满足其灵活管理空间的功能，其结构体内需要一个指针指向我们动态开辟的数组。同样的我们也需要一个成员标识栈顶位置，还需要一个成员存储数组容量上限。

typedef int STDataType;

typedef struct Stack
{
	STDataType* data;
	int top;
	int capacity;
}ST;

2.2?栈的函数接口

2.2.1 栈的初始化

? ? ? ? 当新建一个栈后，我们需要对其结构体进行初始化。将指针值为空，将容量初始化为0，同时将表示栈顶的成员置为-1。top初始化为-1，表示栈顶所在元素下标，-1即为栈为空。也可以将top初始化为0，表示栈内元素个数。此处选择第一种方式。

void STInit(ST* pst)
{
	assert(pst);

	pst->data = NULL;
	pst->top = -1;
	pst->capacity = 0;
}

2.2.2 栈的数据插入（入栈）

? ? ? ? 当要在栈中插入数据时，我们首先要判断是否需要扩容，从而防止越界访问的问题。修改完容量后只需要将数据存储到数组的末端（栈顶）即可。

void STPush(ST* pst,STDataType x)
{
	assert(pst);

	if (pst->top + 1 == pst->capacity)
	{
		int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		STDataType* tmp = realloc(pst->data, newcapacity*sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		pst->data = tmp;
		pst->capacity = newcapacity;
	}
	pst->top++;
	pst->data[pst->top] = x;
}

2.2.3 栈的数据删除（出栈）

? ? ? ? 出栈只需要将top减1即可，注意使用断言限制空指针与越界访问。

void STPop(ST* pst)
{
	assert(pst);
	assert(pst->top != -1);

	pst->top--;
}

2.2.4 判断栈是否为空

? ? ? ? 栈是否为空只需要判断top成员是否为-1即可。

bool STEmpty(ST* pst)
{
	assert(pst);

	return pst->top == -1;
}

2.2.5 取栈顶数据

? ? ? ? 因为top保存的是栈顶的下标，所以取栈顶元素只需要访问该下标元素即可。

STDataType STTop(ST* pst)
{
	assert(pst);
	assert(pst->top != -1);

	return pst->data[pst->top];
}

2.2.6 栈数据统计

? ? ? ? 该接口是为了输出此时栈内的数据个数，只需将栈顶下标加一即可。

int STSize(ST* pst)
{
	assert(pst);

	return pst->top + 1;
}

2.2.7 栈销毁

? ? ? ? 销毁栈需要将其数组空间释放，并将结构体内成员值全部初始化。

void STDestroy(ST* pst)
{
	assert(pst);

	free(pst->data);
	pst->data = NULL;
	pst->capacity = 0;
	pst->top = -1;
}

3. 栈总结反思

? ? ? ? 栈主要实现了“先进后出，后进先出”的特殊功能，这就意味着栈这种数据结构在面对一些满足该特性的一些特殊情况下才能很好的适配。其结构和实现并不复杂，相较于其他数据结构很容易理解，特征也非常明显，处理好一些类似于下标之类的小细节就没问题了。