贪心算法:活动选择问题以及贪心选择性质证明
什么时候使用贪婪算法?
– 贪心选择特性:
全局的最优解可以通过局部的最优(贪婪) 选择得到.
? 动态规划需要检查子问题的解。
– 最优子结构: 问题的最优解包含了其子问题的最优解.
? 例如, 如果 A 是S的最优解, 那么 A ' = A - {1} 是 的最优解.
? 贪心算法 (试探) 并不能总是得到最优解.
? 谈论算法和动态规划 (DP)对比
– 相同: 最优子结构
– 差别: 贪婪选择特性
– 如果贪婪算法不是最优的, 可以使用DP 。
活动选择问题
给定一个集合 S = {1, 2, …, n} n个计划的活动,对每个活动 , 开始时间为
?结束时间为
, 选择出相互兼容的活动最大集合.
– 如果被选中,活动 ?在半开放的区间
中进行.
– 活动 ?和
兼容 如果?
和?
不重叠

问题分析

基本思想

 ?对应伪代码
?对应伪代码

贪心选择性质证明
设为问题所给的活动集合,且E中的活动是按照活动结束时间增序排列的,明显,活动
为最早结束。
设A是问题的一个最优解,明显有A是E的一个子集。这里设A的第一个活动为k
1:若,即A的第一个活动就是最早结束的,故A是以贪心选择开始的最优解。
2:若,设集合
,即用活动
替换掉活动
又因为的结束时间小于
,故
比
提取结束。另外由于A中的活动是相容的,故B中的活动也相容。
又因为A中的活动个数和B中的活动个数相同,故B也是最优解(需要注意的是最优解一般不唯一)。
所以B是一个以贪心选择活动为开始后的最优活动。
之后假设第k步成立,即按照算法选了,现在我们只要证明选
也是最优解解一部分即可。这是需要注意的是,对需要满足相同性,且是选结束时间尽可能早的任务.
利用数学归纳法
1:A包含了算法选择的前k项活动,假设存在活动选择的最优解的即
,如下图所示。

这里将未被选择的活动非为S1和S2两个部分。
值得注意的是,B一定来自于S1,因为S2的所有活动都与A冲突,为了满足相容性,不能被选到。
假设B不是S1的最优解,即S1存在有最优解B'的活动数多于B;
那么第k步的最优解就变为AUB',显然与开始AUB为最优解的假设是矛盾的,因此不成立。
2:证明选结束时间最早的活动,也是最优解。
在S1中,必定存在一个结束时间最早的活动,即
在A的第一个活动为k时的证明可知,算法的第一步的最优解包含结束时间最早的活动。

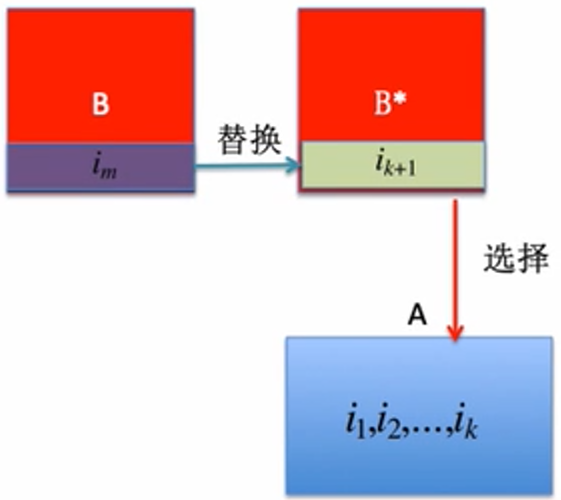
因此S1存在最优解B*包含了活动。B和B*都是S1的最优解。因此两者包含的活动个数相同。
用B*代替B,即AUB的活动与AUB*的活动个数相同,因此最优解的性质不变。

而B*包含了,故证明了AUB*是最优的,所以根据数学归纳法,假设算法的前k项活动是最优的,选第k+1项也是最优解,命题得证。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!