C++线性表
线性表的定义及其运算
线性表是一种最简单、最基本也是最常用的线性结构。在线性结构中，数据元素之间存在一个对一个的线性关系，数据元素“一个接一个地排列”。在一个线性表中，数据元素的类型是相同的，或者说，线性表是由同一类型的数据元素构成的。在实际问题中，线性表的例子很多，如学生自然情况信息表、工资信息表等都是线性表。
线性表是具有相同数据类型的n(n≥0)个数据元素的有限序列，通常记为：（a1,a2, …, ai-1, ai, ai+1, …, an）。其中，n为数据元素个数，称为表长。当n=0时称为空表。
表中相邻元素之间存在顺序关系。将ai-1称为ai的直接前驱，ai+1称为ai的直接后继。也就是说，对于ai，当i=2, …, n时，有且仅有一个直接前驱ai-1；当i=1,2, …,n-1时，有且仅有一个直接后继ai+1。a1是表中第一个数据元素，它没有前驱；an是最后一个数据元素，它无后继。
线性表的基本运算如下：
（1）线性表的初始化：void Initiate()
初始条件：线性表不存在。
操作结果：构造一个空的线性表。
（2）求线性表的长度：int Length()
初始条件：线性表已存在。
操作结果：返回线性表所含数据元素的个数。
（3）取表元：DataType Get(int i)
初始条件：表存在且1≤i≤Length()。
操作结果：返回线性表的第i个数据元素的值。
（4）按值查找：int Locate(DataType x)
初始条件：线性表已存在，x是给定的一个数据元素。
操作结果：在线性表中查找值为x的数据元素，返回首次出现的值为x的那个数据元素的序号，称为查找成功；如果未找到值为x的数据元素，返回0表示查找失败。
（5）插入操作：int Insert(DataType x, int i)
初始条件：线性表已存在。
操作结果：在线性表的第i个位置上插入一个值为x的新元素，使原序号为i,i+1, …,n的数据元素的序号变为i+1,i+2, …,n+1，插入后表长=原表长+1，返回1表示插入成功；若线性表L中数据元素个数少于i-1个，则返回0表示插入失败。
（6）删除操作：int Deleted(int i)
初始条件：线性表已存在。
操作结果：在线性表L中删除序号为i的数据元素，删除后使序号为i+1, i+2, …, n的元素变为序号i, i+1, …, n-1，新表长=原表长-1，返回1；若线性表中数据元素个数少于i，则返回0表示删除失败。
线性表的顺序存储结构
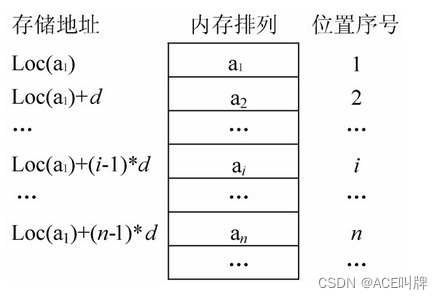
线性表的顺序存储结构是指在内存中用一组地址连续的存储空间顺序存放线性表的各数据元素，使得逻辑关系上相邻的数据元素在物理位置上也相邻。采用这种存储形式存储的线性表称为线性表的顺序存储结构，简称顺序表。
线性表的顺序存储结构就是线性表中数据的内存空间都是连续的，所有数据不仅在逻辑上是相邻的，物理意义上也是相邻的
因为内存空间是连续的，所以设数据元素a1的存储地址为Loc(a1)，每个数据元素占用d个存储地址，则第i个数据元素的地址为：
Loc(ai)=Loc(a1)+(i-1)*d (1 <= i <= n)
也就是说，只要知道顺序表的首地址和每个数据元素所占用地址单元的个数，就可以求出第i个数据元素的地址。这也是顺序表具有按数据元素的序号随机存取的特点。
顺序表中数据元素及其存储位置示意图：
在程序设计语言中，一维数组的数据在内存中是一段连续的内存空间，所以可以用数组来表示顺序表的数据存储区域。
考虑到线性表中的插入、删除运算，所以线性表的长度也会不停的发生变化，数组的容量要设计的足够大，假设用data[MAXSIZE]表示，其中MAXSIZE是一个根据实际问题定义的足够大的整数，但是存放当前线性表元素的个数可能达不到MAXSIZE大小，所以需要一个变量len来记录当前线性表的长度，始终指向线性表中最后一个元素的下一个位置，其值为最后一个数据元素的位置值，若该表为空表，则len=0。
顺序表的数据类型定义如下：
#pragma once
#define MAXSIZE 100
// 学生表
struct Student
{
int id_; // 学生id
std::string name_; // 学生姓名
int score_; // 学生成绩
Student()
: id_(0), score_(0)
{}
};
class SequenList
{
public:
// 初始化线性表
void Initiate();
private:
Student stu_[MAXSIZE];
int len_;
};
初始化运算
// 顺序表的初始化即构造一个数据元素个数为0的空表
void SequenList::Initiate()
{
len_ = 0;
}
插入运算
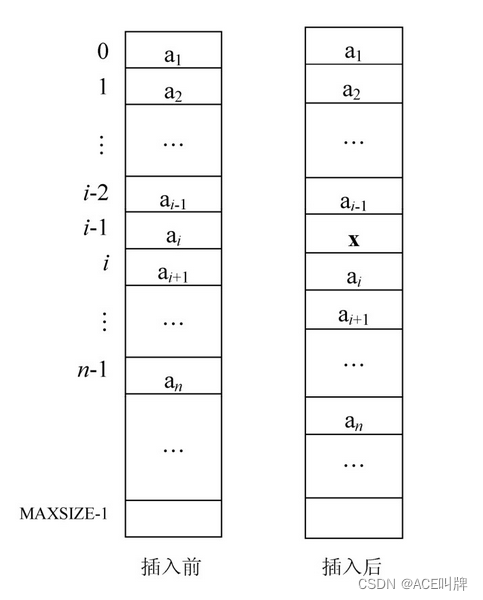
顺序表的插入运算是指在顺序表的第i个位置上插入一个值为x的新元素，插入后使原表为n的顺序表（a1, a2, …, ai-1, ai, ai+1, …, an）变为表长为n+1的顺序表（a1, a2, …, ai-1, x, ai, ai+1, …, an）其中，i的合理取值范围为1 ≤ i ≤ n+1。
顺序表插入示意图如下：
bool SequenList::Insert(Student x, int i)
{
if (len_ >= MAXSIZE)
{
std::cout << "顺序表已满" << std::endl;
return false;
}
else if ((i < 1) || i > (len_ + 1))
{
std::cout << "插入位置不合法" << std::endl;
return false;
}
else
{
for (int j = len_; j >= i; j--)
stu_[j] = stu_[j - 1];
stu_[i - 1] = x;
len_++;
return true;
}
}
插入运算的时间性能分析
顺序表的插入运算时间主要浪费在数据的移动，在第i个位置上插入x，从第i个到第n个元素都要向后移动一个位置，共需要移动n-(i-1)，即n-i+1个数据元素。而i的取值范围为
1 ≤ i ≤ n+1，即有n+1个位置可以插入。所以时间复杂度为O(n)。
删除运算
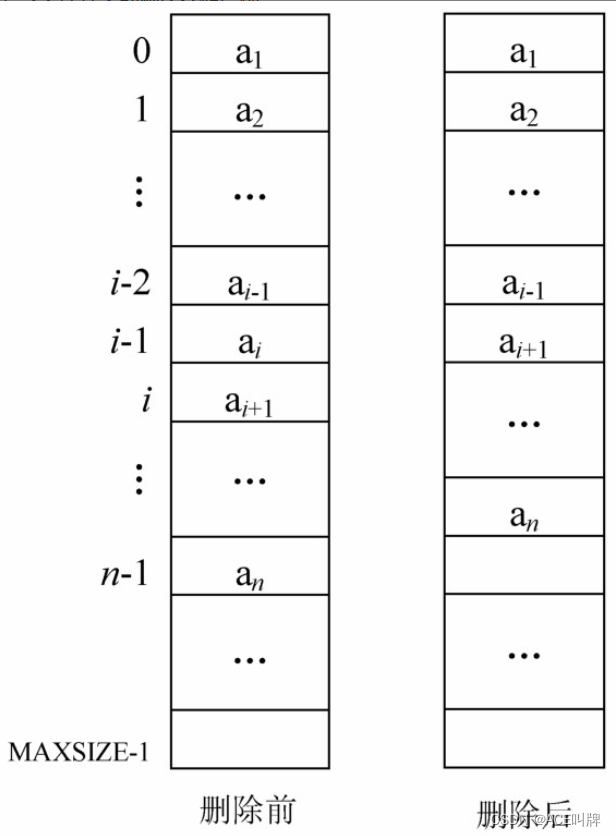
线性表的删除运算是指将表中第i个元素从线性表中删除，使原表长为n的线性表（a1,a2, …,ai-1,ai,ai+1, …,an）变成表长为n-1的线性表（a1, a2, …, ai-1, ai+1, …, an）i的取值范围为1 ≤ i ≤ n。
顺序表的删除示意图如下：
bool SequenList::Delete(const int& i)
{
if (i < 1 && i > len_)
{
std::cout << "删除位置不合法" << std::endl;
return false;
}
else
{
for (int j = i; j < len_; j++)
stu_[j - 1] = stu_[j];
len_--;
return true;
}
return false;
}
同理，删除数据也需要移动数据，平均时间复杂度为O(n)。
按值查找
顺序表中的按值查找是指在线性表中查找与给定值x相等的数据元素。在顺序表中完成该运算最简单的方法是：从第一个元素a1起依次和x比较，直到找到一个与x相等的数据元素，则返回它在顺序表中的位置值（下标+1）；或者查遍整个表都没有找到与x相等的数据元素，则返回0。
Student SequenList::Locate(const int& _id)
{
for (int j = 0; j < len_; j++)
{
if (stu_[j].id_ == _id)
return stu_[j];
}
return Student();
}
本算法的主要运算是比较。显然，比较的次数与x在表中的位置有关，也与表长有关。当a1=x时，比较一次成功；当an=x时，比较n次成功。在查找成功的情况下，平均比较次数为（n+1）/2，时间复杂度为O(n)。
读取第i个元素的值
Student SequenList::Get(const int& i)
{
if (i < 1 || i > len_)
{
std::cout << "查找位置不合法" << std::endl;
return Student();
}
return stu_[i - 1];
}
取得数据元素个数
int SequenList::GetLength()
{
return len_;
}
线性表的链式存储结构
顺序表的存储特点是在物理位置上元素的存储地址连续，因此，对顺序表元素的插入、删除需要通过移动实现，大大降低了效率。
线性表的链式存储结构不需要用地址连续的存储单元来实现，因为它不要求逻辑关系上相邻的两个数据元素物理位置上也相邻。它通过“链”建立起数据元素之间的逻辑关系。因此对线性表的插入、删除不需要移动数据元素。
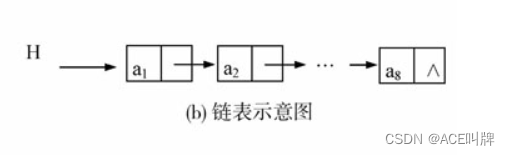
单链表结构
链表的元素的内存空间是不连续的，那么要想实现线性结构，需要在每个数据元素中存放一个指针，这个指针指向下一个元素的地址，这样的一个结构称为结点。
定义链表
// 学生表
struct Student
{
int id_; // 学生id
std::string name_; // 学生姓名
int score_; // 学生成绩
Student(int _id, std::string _name, int _score)
: id_(_id), score_(_score), name_(_name)
{}
Student()
: id_(0), score_(0)
{}
};
class Item
{
public:
Link* next_;
Student stu_;
Item()
{
next_ = nullptr;
}
};
class Link
{
public:
Link();
~Link();
void Initiate(); //初始化
void DeleteAll(); //删除所有结点
void HeadCreate(int n); //从头建链表
void TailCreate(int n); //从尾建链表
void HeadCreateWithHead(int n); //建立带表头的链表(从头)
void TailCreateWithHead(int n); //建立带表头的链表(从尾)
int Length(); //求链表长度
Item ＊Locatex(Student x); //查找值为x的数据元素
Item ＊Locatei(int i); //查找第i个元素
bool Insert(Student x, int i); //在链表第i个结点之前插入x
bool Deleted(int i); //删除链表中第i个结点
void Print(); //打印链表
private:
Item* item_; // 链表头指针
};
单链表的运算
1、初始化
void Link::Initiate()
{
DeleteAll();
head_ = nullptr;
}
2、建立单链表
（1）头插法：从表尾到表头建立单链表（不带有空白头结点）
因为是在链表的头部插入，读入数据的顺序和线性表中的逻辑顺序是相反的。
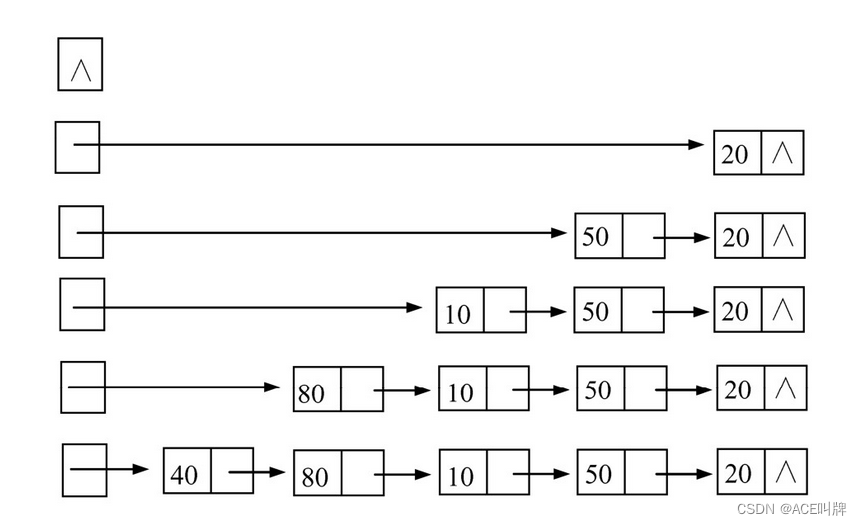
void Link::HeadCreate(int n)
{
DeleteAll();
Item* s = nullptr, *p = nullptr;
for (int i = 0; i < n; i++)
{
s = new Item;
s->stu_ = Student(i, "ss", i * 10 + 1);
s->next_ = p;
p = s;
}
head_ = p;
}
（2）尾插法：从表头到表尾建立单链表（不带有空白头结点）
因为是在链表的尾部插入，读入数据的顺序和线性表中的逻辑顺序是相同的。
void Link::TailCreate(int n)
{
DeleteAll();
Item* s = nullptr, * p = nullptr, * r = nullptr;
for (int i = 0; i < n; i++)
{
s = new Item;
s->stu_ = Student(i, "tailCreate", i * 20 + 1);
s->next_ = nullptr;
if (!p)
p = r = s;
else
{
r->next_ = s;
r = s;
}
}
head_ = p;
}
上述两种插入方法是头结点不是空白结点，这种链表在某些情况下不好处理，在链表中插入结点时，将结点插在第一个位置和其他位置是不同的；在链表中删除结点时，删除第一个结点和删除其他结点的处理也是不同的；为了方便操作，有时在链表的头部加入一个空白的“头结点”，头结点的类型与数据结点一致，数据域为空，在标识链表的头指针变量H中存放该结点的地址。这样即使是空表，头指针变量H也不再为空了。头结点的加入使得“第一个结点”的问题不再存在，也使得“空表”和“非空表”的处理成为一致。
3）头插法：从表尾到表头建立单链表（带有空白头结点）
void Link::HeadCreateWithHead(int n)
{
DeleteAll();
Item* s = nullptr, * p = new Item;
p->next_ = nullptr;
for (int i = 0; i < n; i++)
{
s = new Item;
s->stu_ = Student(i, "headCreateWithHead", i * 30 + 3);
s->next_ = p->next_; // 1
p->next_ = s; // 2
}
head_ = p;
}
示意图如下：其中1和2的代码顺序不能变
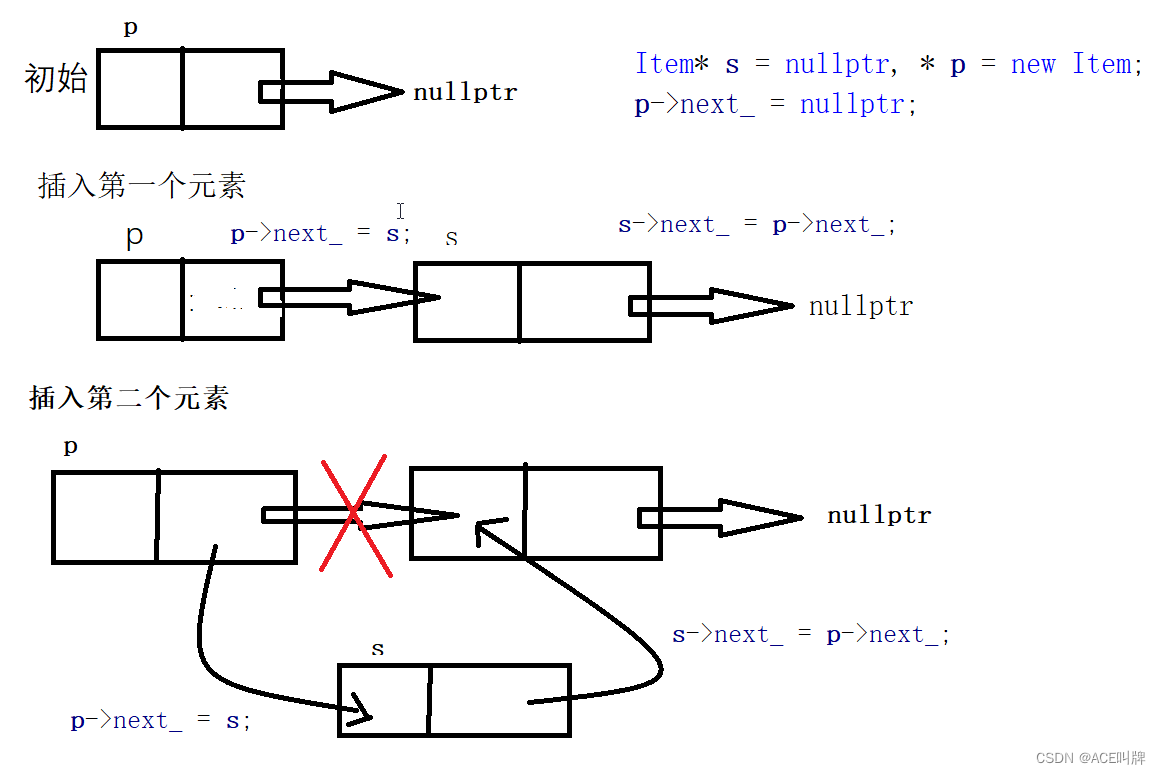（4）尾插法：从表头到表尾建立单链表（带有空白头结点）
void Link::TailCreateWithHead(int n)
{
DeleteAll();
Item* s = nullptr, *r = nullptr, * p = new Item;
p->next_ = nullptr;
r = p;
for (int i = 0; i < n; i++)
{
s = new Item;
s->stu_ = Student(i, "tailCreateWithHead", i * 30 + 4);
r->next_ = s;
r = s;
}
head_ = p;
}
没有特殊说明的话，以下所有单链表都是带有空白结点
3．求表长
顺序表的表长可以方便获得。相比而言，求单链表的表长稍微复杂些。设有一个移动指针p和计数器j，初始化后，p所指结点后面若还有结点，p向后移动，计数器加1。
int Link::Length()
{
int count = 0;
Item* temp = head_;
while (temp->next_)
{
count++;
temp = temp->next_;
}
return count;
}
4．查找操作
（1）按序号查找
从单链表的第一个元素结点起，判断当前结点是否是第i个，若是，则返回该结点的指针；否则继续下一个结点的查找，直到表结束为止。若没有第i个结点，则返回空；如果i=0；则返回头指针。
Item* Link::Locatei(int i)
{
if (i == 0)
return head_;
Item* p = head_->next_;
int j = 1;
while (!p && j < i)
{
p = p->next_;
j++;
}
if (j == i)
return p;
std::cout << "查找位置大于链表长度" << std::endl;
return nullptr;
}
（2）按值查找
即定位从链表的第一个元素结点起，判断当前结点值是否等于x，若是，返回该结点的指针，否则继续下一个结点的查找，直到表结束为止。若找不到，则返回空。
根据学生id查找
Item* Link::Locatex(Student x)
{
Item* p = p->next_;
while (!p)
{
if (p->stu_.id_ == x.id_)
return p;
p = p->next_;
}
std::cout << "没有该元素" << std::endl;
return nullptr;
}
5．插入
（1）后插结点
设p指向单链表中某结点，s指向待插入的值为x的新结点，将s插入p的后面，插入示意图如下：
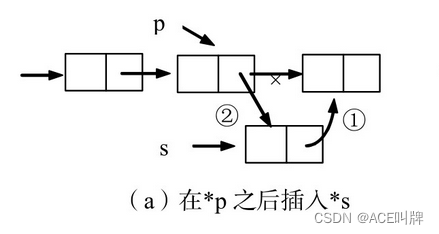操作如下：
s->next = p->next;
p->next = s;
注意：上述操作顺序不能反
（2）前插结点
设p指向链表中某结点，s指向待插入的值为x的新结点，将s插入p的前面，插入示意图如图所示。与后插不同的是，首先要找到＊p的前驱＊q，再完成在q之后插入s。设单链表头指针为L，操作如下：
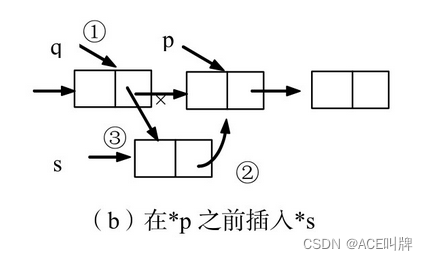
q=L;
while(q->next! =p)
q=q->next; //找*p的直接前驱
s->next=q->next;
q->next=s;
后插操作的时间复杂度为O(1)，前插操作因为要找p的前驱，时间复杂度为O(n)。其实，我们关心的是数据元素之间的逻辑关系，所以仍然可以将s插入*p的后面，然后将p->data与s->data交换即可。这样既满足了逻辑关系，也能使得时间复杂度为O(1)。
（3）插入算法
① 找到第i-1个结点；若存在，继续步骤②，否则结束。
② 申请新结点，将数据填入新结点的数据域。
③ 将新结点插入。
bool Link::Insert(Student x, int i)
{
// 通过位置查找到结点
Item* p = Locatei(i);
if (!p)
return false;
Item* s = new Item;
s->stu_ = x;
s->next_ = p->next_;
p->next_ = s;
return true;
}
6、删除
① 找到第i-1个结点，若存在，继续步骤②，否则结束。
② 若存在第i个结点，则继续步骤③，否则结束。
③ 删除第i个结点，结束。
bool Link::Deleted(int i)
{
// 找到前驱结点
Item* p = Locatei(i - 1);
if (!p)
return false;
Item* q = p->next_;
if (!q)
return false;
p->next_ = q->next_;
delete q;
q = nullptr;
return true;
}
7．打印
void Link::Print()
{
Item* p = head_->next_;
while (p)
{
std::cout << p->stu_.id_ << " " << p->stu_.name_ << " " << p->stu_.score_ << std::endl;
p = p->next_;
}
return;
}
8．删除所有结点
void Link::DeleteAll()
{
Item* p = nullptr;
while (head_)
{
p = head_->next_;
delete head_;
head_ = p;
}
return;
}
通过上面的基本操作可知：
① 在单链表上插入、删除一个结点，必须知道其前驱结点的指针；
② 单链表不具有按序号随机访问的特点，只能从头指针开始一个个顺次进行。
循环链表结构
单链表结构下最后一个结点的指针域指向空，循环链表结构的最后一个结点的指针域指向第一个结点。
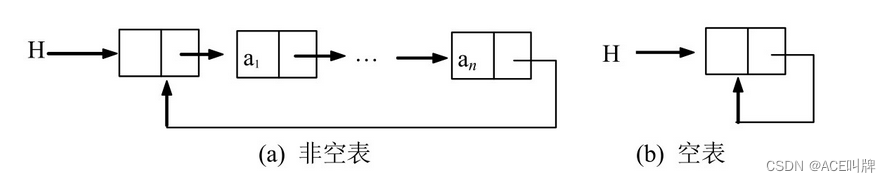
在循环单链表上的操作基本上与非循环链表相同，只是将原来判断指针是否为NULL变为是否是头指针，没有其他较大的变化。
对于单链表，只能从头结点开始遍历整个链表；而对于循环单链表，则可以从表中任意结点开始遍历整个链表。
不仅如此，有时对链表常做的操作是在表尾、表头之间进行。此时可以改变链表的标识方法，不用头指针而用一个指向尾结点的指针R来标识，可以使操作效率得以提高。
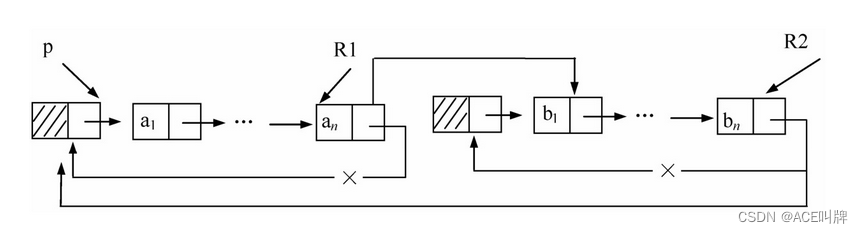
例如，对两个循环单链表H1、H2的连接操作，是将H2的第一个数据结点接到H1的尾结点。如用头指针标识，则需要找到第一个链表的尾结点，其时间复杂度为O(n)；而链表若用尾指针R1、R2标识，则时间复杂度为O(1)。操作如下：
p= R1->next; //保存R1的头结点指针
R1->next=R2->next->next; //头尾连接
delete R2->next; //释放第二个表的头结点
R2->next=p; //组成循环链表
双向链表结构
单链表结构里有一个指针指向当前结点后继结点，双向链表结构多了一个指针指向当前结点的前驱结点。
双向链表结构的结点定义：
class Item
{
public:
Item* next_;
Item* prior_;
Student stu_;
Item()
{
next_ = nullptr;
prior_ = nullptr;
}
};
带头结点的双向循环链表示意图如下，显然，通过某结点的指针p既可以直接得到它的后继结点的指针p->next，也可以直接得到它的前驱结点的指针p->prior。这样在有些操作中需要找前驱结点时，无须再用循环。
设p指向双向循环链表中的某一结点，即p是该结点的指针，则p->prior->next表示的是p结点的前驱结点的后继结点的指针，即与p相等；类似，p->next->prior表示的是p结点的后继结点的前驱结点的指针，也与p相等。所以有以下等式：
p->prior->next = p = p->next->prior
1．双向链表中结点的插入
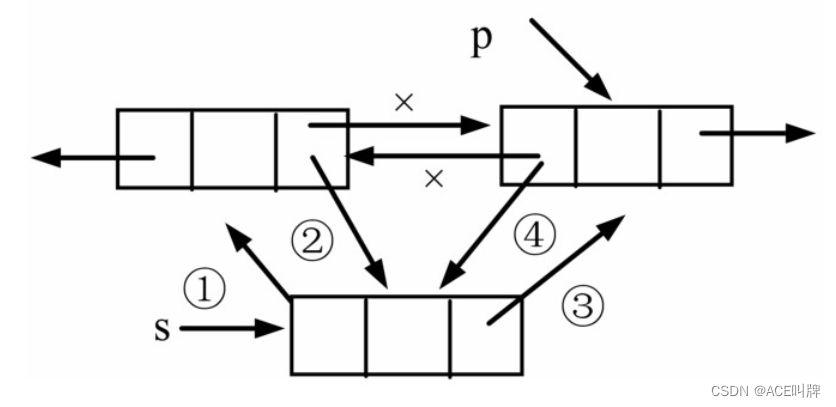
设p指向双向链表中某结点，s指向待插入的值为x的新结点，将s插入p的前面，插入示意图如下：
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;
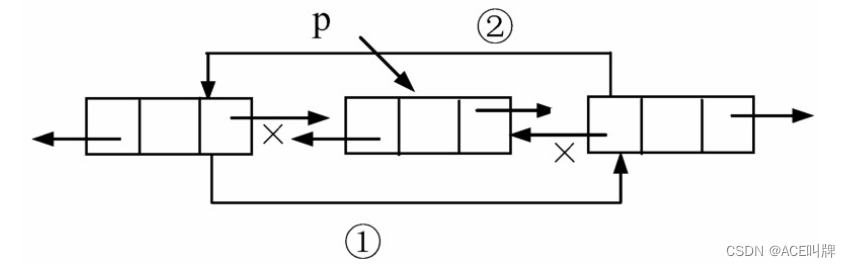
2．双向链表中结点的删除
设p指向双向链表中某结点，删除*p。操作示意图如下：
操作如下：
p->prior->next=p->next;
p->next->prior=p->prior;
delete p;
顺序表和链式表的比较
顺序表的优点：
- 实现简单，大多数开发语言都支持数组
- 减少开销：不需要开辟结点
- 可以按元素序号随机访问元素
缺点：
- 在顺序表中进行插入、删除的操作时需要移动元素，时间复杂度为O(n)，表中元素较多时影响效率。
- 需要预先分配足够大的存储空间，估计的过大，可能会导致顺序表空间大量闲置；预先分配过小，又会造成溢出。
链式表的优缺点恰好与顺序表相反。
怎么选择？
当需要频繁的插入、删除操作时选择链式表，需要随机访问元素时选择顺序表。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！