代码随想录算法训练营Day10|232.用栈实现队列、225. 用队列实现栈

---

理论基础

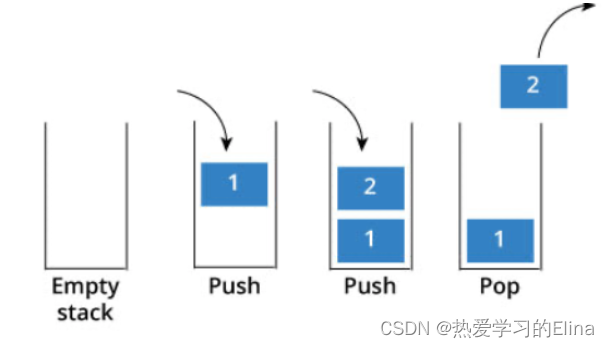
队列是先进先出，栈是先进后出。Java中的栈与队列介绍可以访问链接：Java数据结构中的栈和队列（带图解）

Stack方法：

方法	功能
Stack()	构造一个空栈
E push(E e)	将e入栈，并返回e
E pop()	将栈顶元素出栈并返回
E peek()	获取栈顶元素
int size()	获取栈中有效元素个数
boolean empty()	检测栈是否为空

Queue方法：

方法	功能
boolean o?er(E e)	入队列
E poll()	出队列
peek()	获取队列头元素
int size()	获取队列中有效元素个数
boolean empty()	检测队列是否为空

---

一、232.用栈实现队列

题目描述： 使用栈实现队列的下列操作：
push(x) – 将一个元素放入队列的尾部。
pop() – 从队列首部移除元素。
peek() – 返回队列首部的元素。
empty() – 返回队列是否为空。

1. 双栈

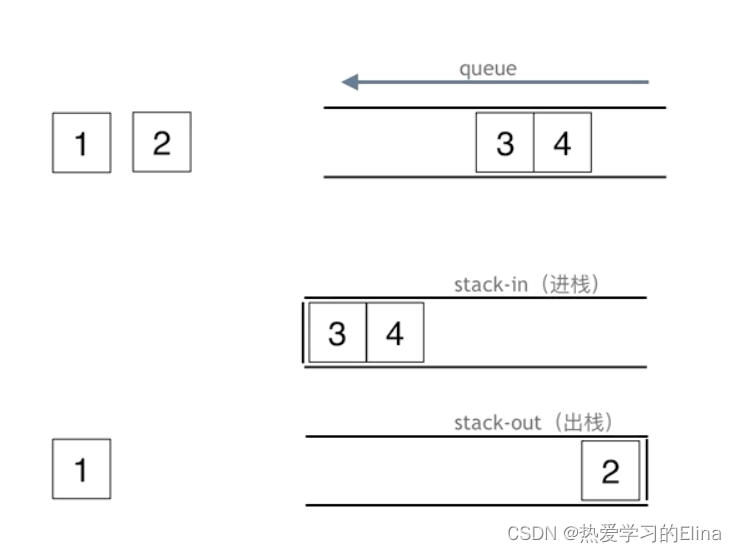
将一个栈作为输入栈，用于压入push传入的数据；另一个栈作为输出栈，用于pop和peak操作。
每次pop和peak时，若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈，这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。

• 时间复杂度：$O(1)$
• 空间复杂度：$O(n)$

class MyQueue {
    Deque<Integer> inStack;
    Deque<Integer> outStack;

    public MyQueue() {
        inStack = new ArrayDeque<Integer>();
        outStack = new ArrayDeque<Integer>();
    }
    
    public void push(int x) {
        inStack.push(x);
    }
    
    public int pop() {
        if (outStack.isEmpty()) {
            in2out();
        }
        return outStack.pop();
    }
    
    public int peek() {
        if (outStack.isEmpty()) {
            in2out();
        }
        return outStack.peek();
    }
    
    public boolean empty() {
        return inStack.isEmpty() && outStack.isEmpty();
    }

    private void in2out() {
        while (!inStack.isEmpty()) {
            outStack.push(inStack.pop());
        }
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

二、225. 用队列实现栈

题目描述： 使用队列实现栈的下列操作：
push(x) – 元素 x 入栈
pop() – 移除栈顶元素
top() – 获取栈顶元素
empty() – 返回栈是否为空

1. 两个队列

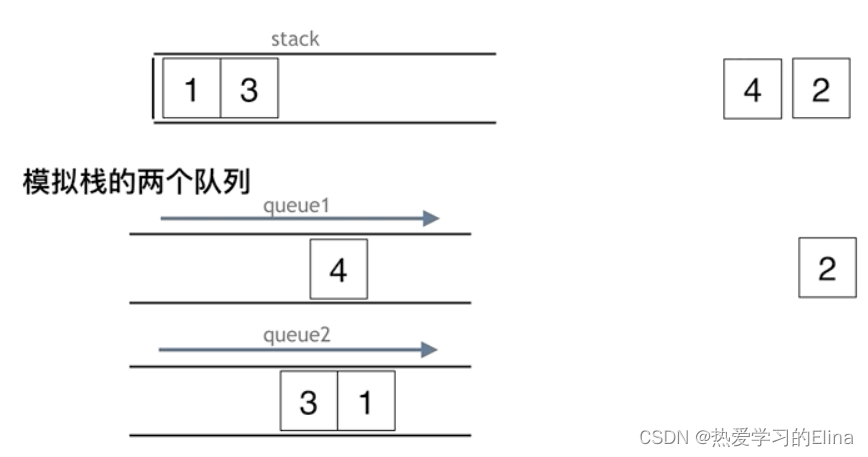
1. 为了满足栈的特性，即最后入栈的元素最先出栈，在使用队列实现栈时，应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作，其中 queue1 用于存储栈内的元素，queue2 作为入栈操作的辅助队列。
2. 入栈操作时，首先将元素入队到 queue2，然后将 queue1 的全部元素依次出队并入队到 queue2，此时 queue2 的前端的元素即为新入栈的元素，再将 queue1 和 queue2互换，则 queue1 的元素即为栈内的元素，queue1 的前端和后端分别对应栈顶和栈底。
3. 由于每次入栈操作都确保 queue1 的前端元素为栈顶元素，因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除 queue1 的前端元素并返回即可，获得栈顶元素操作只需要获得 queue1 的前端元素并返回即可（不移除元素）。由于 queue1 用于存储栈内的元素，判断栈是否为空时，只需要判断 queue1 是否为空即可。

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

class MyStack {
    Queue<Integer> queue1;
    Queue<Integer> queue2;

    public MyStack() {
        queue1 = new LinkedList<Integer>();
        queue2 = new LinkedList<Integer>();
    }
    
    public void push(int x) {
        queue2.offer(x);
        while (!queue1.isEmpty()) {
            queue2.offer(queue1.poll());
        }
        Queue<Integer> temp = queue1;
        queue1 = queue2;
        queue2 = temp;
    }
    
    public int pop() {
        return queue1.poll();
    }
    
    public int top() {
        return queue1.peek();
    }
    
    public boolean empty() {
        return queue1.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

2. 一个队列

此过程简言之：队尾元素去队头，通过一个类似循环的方式形成栈。详细描述如下：

1. 使用一个队列时，为了满足栈的特性，即最后入栈的元素最先出栈，同样需要满足队列前端的元素是最后入栈的元素。
2. 入栈操作时，首先获得入栈前的元素个数 n，然后将元素入队到队列，再将队列中的前 n 个元素（即除了新入栈的元素之外的全部元素）依次出队并入队到队列，此时队列的前端的元素即为新入栈的元素，且队列的前端和后端分别对应栈顶和栈底。
3. 由于每次入栈操作都确保队列的前端元素为栈顶元素，因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可，获得栈顶元素操作只需要获得队列的前端元素并返回即可（不移除元素）。
4. 由于队列用于存储栈内的元素，判断栈是否为空时，只需要判断队列是否为空即可。

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

class MyStack {
    Queue<Integer> queue;

    public MyStack() {
        queue = new LinkedList<Integer>();
    }

    public void push(int x) {
        int n = queue.size();
        queue.offer(x);
        for (int i = 0; i < n; i++) {
            queue.offer(queue.poll());
        }
    }

    public int pop() {
        return queue.poll();
    }

    public int top() {
        return queue.peek();
    }

    public boolean empty() {
        return queue.isEmpty();
    }
}

---

总结

以上就是今天学习的内容，掌握 队列是先进先出，栈是先进后出 原则。