NNDL 作业10 BPTT [HBU]

2023-12-13 15:45:26

习题6-1P 推导RNN反向传播算法BPTT.

习题6-2 推导公式(6.40)和公式(6.41)中的梯度．

习题6-3 当使用公式(6.50)作为循环神经网络的状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决方法．

没理解的部分：

习题6-2P 设计简单RNN模型，分别用Numpy、Pytorch实现反向传播算子，并代入数值测试.

顺便复习一下tanh激活函数的性质

老师布置作业原博客链接：【23-24 秋学期】NNDL 作业10 BPTT-CSDN博客

习题6-1P 推导RNN反向传播算法BPTT.

循环神经网络的参数通过梯度下降方法学习，以随机梯度下降为例，给定一个训练样本(x,y),其中:

长度为T的输入序列为: $x_{1:T}=(x_{1},...,x_{T})$

长度为T的标签序列为: $y_{1:T}=(y_{1},...y_{T})$

即在每个时刻t，都有一个监督信息 $y_{t}$ ，定义时刻t的损失函数为： $L_{t}=L(y_{t},g(h_{t}))$

(其中 $g(h_{t})$ 为第t时刻的输出，L为可微分的损失函数)

那么整个序列的损失函数为: $L=\sum_{t=1}^{T}L_{t}$

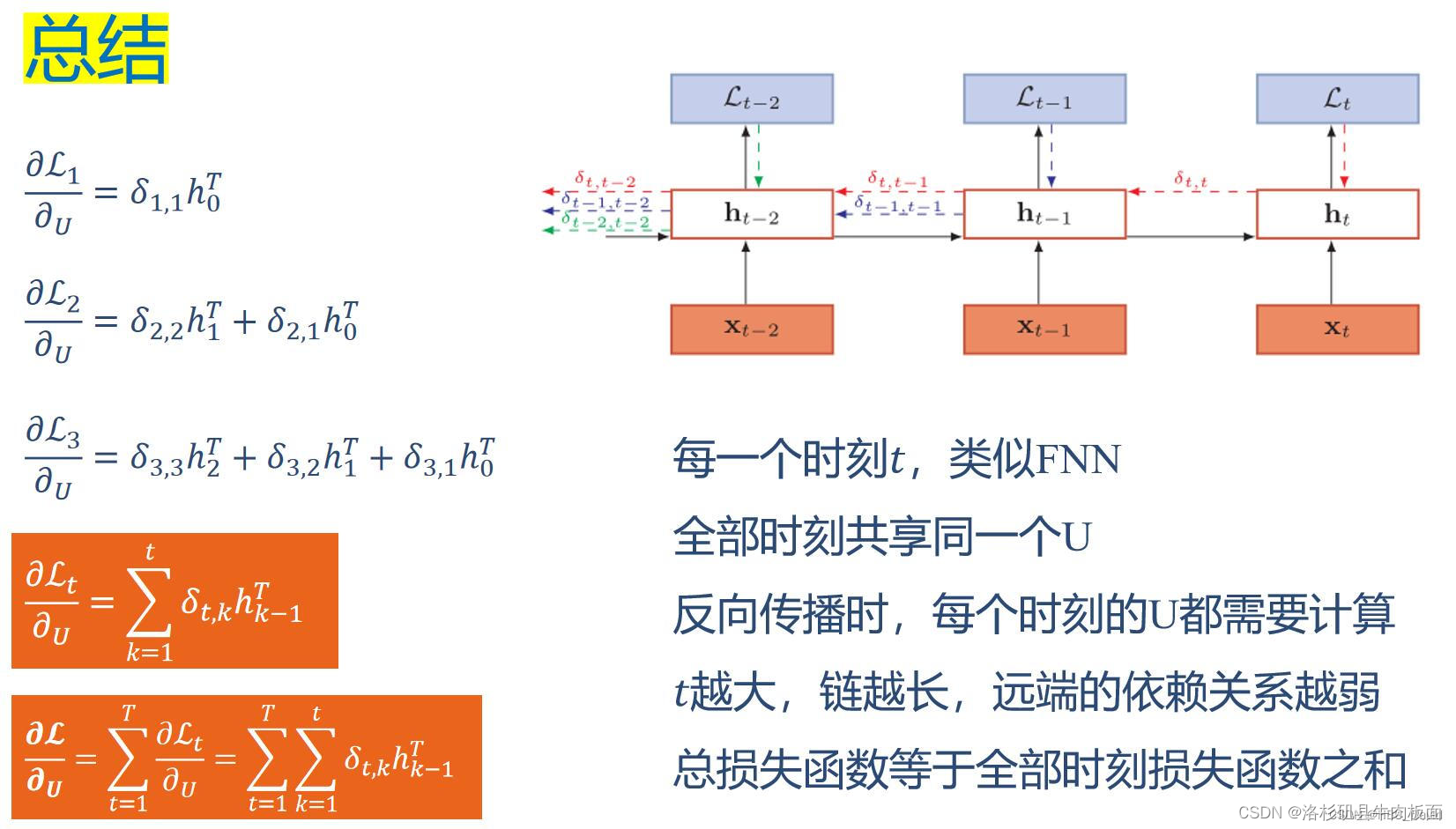
整个序列的损失函数L关于参数U的梯度为： $\frac{\partial L}{\partial U}=\sum_{t=1}^{T}\frac{\partial L_{t}}{\partial U}$

即每个时刻损失 $L_{t}$ 对参数U的偏导数之和。

随时间反向传播(BackPropagation Through Time,BPTT)算法的主要思想是通过类似前馈神经网络的错误反向传播算法来计算梯度。由于循环神经网络中所有层的参数是共享的，因此参数的真实梯度是所有"展开层"的参数梯度之和。

首先来计算第t时刻损失对参数U的偏导数 $\frac{\partial L_{t}}{\partial U}$ :

参数:? U

隐藏层所在的每个时刻:?? $k(1\leq k\leq t)$

净输入:?? $z_{k}=Uh_{k-1}+Wx_{k}+b$

第t时刻的损失函数 $L_{t}$ 关于参数 $u_{ij}$ 的梯度为：(参数U是二维矩阵，所以有i、j维度):

$\frac{\partial L_{t}}{\partial u_{ij}}=\sum_{k=1}^{t}\frac{\partial^{+} z_{k}}{\partial u_{ij}}\frac{\partial L_{t}}{\partial z_{k}}$

对 $u_{ij}$ 进行求偏导数，得到公式1:

$\frac{\partial^{+} z_{k}}{\partial u_{ij}}=[0,...,[h_{k-1}]_{j},...,0] \doteq\mathbb{I}_{i}([h_{k-1}]_{j})$

其中 $[h_{k-1}]_{j}$ 为第k-1时刻隐状态的第j维； $\mathbb{I}_{i}(x)$ 表示除了第i行值为x外，其余都为0的行向量。(第二个等号上面的符号应该是▲，但是公式编辑器里没有，就用'? .? '代替了)

定义误差项 $\delta _{t,k}=\frac{\partial L_{t}}{\partial z_{k}}$ 为第t时刻的损失对第k时刻隐藏神经层的净输入 $z_{k}$ 的导数，则当 $1\leq k< t$ 时，得到公式2：

$\delta _{t,k}=\frac{\partial L_{t}}{\partial z_{k}}=\frac{\partial h_{k}}{\partial z_{k}}\frac{\partial z_{k+1}}{\partial h_{k}}\frac{\partial L_{t}}{\partial z_{k+1}} =diag(f^{'}(z_{k}))U^{T}\delta _{t,k+1}$

将公式1，公式2代入到第t时刻的损失函数 $L_{t}$ 关于参数 $u_{ij}$ 的梯度公式中得到：

$\frac{\partial L_{t}}{\partial u_{ij}}=\sum_{k=1}^{t}[\delta _{t,k}]_{i}[h_{k-1}]_{j}$

将上式写为矩阵形式，得到公式3:

$\frac{\partial L_{t}}{\partial U}=\sum_{k=1}^{t}\delta _{t,k}h_{k-1}^{T}$

将公式3代入到?整个序列的损失函数L关于参数U的梯度公式 $\frac{\partial L}{\partial U}=\sum_{t=1}^{T}\frac{\partial L_{t}}{\partial U}$ 中，最终得到以下式子：

$\frac{\partial L}{\partial U}=\sum_{t=1}^{T}\sum_{k=1}^{t}\delta _{t,k}h_{k-1}^{T}$

总结：(来自老师分享的PPT，有图有公式，方便理解)

(实在不会推的公式，就先背下来。)

习题6-2 推导公式(6.40)和公式(6.41)中的梯度．

同上一问算法步骤，我们进行以下推导：

对于公式(6.40)，L关于权重W的梯度的推导：

对于公式(6.41)，L关于偏置b的梯度的推导：

习题6-3 当使用公式(6.50)作为循环神经网络的状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决方法．

参考博客：

(这位博主讲的很清楚！！非常推荐精读)

以上是邱锡鹏《神经网络与深度学习》一书中的内容，其中的(6.50)是解决长程依赖--梯度消失问题所做出的模型改进公式。

因为拍的照片不是特别清晰，我再总结一下：
为了解决循环神经网络长程依赖问题的? 梯度消失和梯度爆炸问题，我们可以采取以下的措施：

针对梯度爆炸：通过权重衰减、梯度截断来实现，梯度爆炸问题比较容易解决。

针对梯度消失： 改变模型，或使用一些优化技巧。

发生梯度消失和梯度爆炸的原因：无论是梯度消失还是梯度爆炸，都是源于网络结构太深，造成网络权重不稳定，从本质上来讲是因为梯度反向传播中的连乘效应

公式(6.34)为对误差项的偏导数：

$\delta_{t,k}=\frac{\partial L_{t}}{\partial z_{k}}=diag(f^{'}(z_{k}))U^{T}\delta_{t,k+1}$

公式(6.50)：? ?? $h_{t}=h_{t-1}+g(x_{t},h_{t-1};\Theta )$

$Z_k=Uh_{k-1}+W_{x_k}+b$ 为在第K时刻函数g(.)的输入，在计算公式（6.34）中的误差项时，梯度可能过大，从而导致了梯度爆炸问题。

解决方式：1.更换激活函数，比如可以选择ReLu函数? 2.更改RNN隐藏层的结构，比如采用GRU或者LSTM门控机制的隐藏层结构。

没理解的部分：

*其实这道题我没有完全理解，因为涉及到的数学公式太复杂，要求的数学功底高，我看不明白(去QQ上联系了老师，老师说先和舍友同学们讨论讨论，期末考试前再为我做答疑)。插个眼，想明白了再继续更新

习题6-2P 设计简单RNN模型，分别用Numpy、Pytorch实现反向传播算子，并代入数值测试.

REF:?L5W1作业1 手把手实现循环神经网络-CSDN博客

RNN CELL类 构建的流程：

代码(跟着参考代码手敲了一遍，每一步的注释都标清楚了，方便理解)：

import torch
import numpy as np

class RNNCell:
    #初始化RNN单元的属性
    def __init__(self, weight_ih, weight_hh,
                 bias_ih, bias_hh):

        #输入和隐藏状态的权重矩阵
        self.weight_ih = weight_ih
        self.weight_hh = weight_hh

        #输入和隐藏状态的偏置
        self.bias_ih = bias_ih
        self.bias_hh = bias_hh

        self.x_stack = [] #存储输入输入
        self.dx_list = [] #存储对输入的梯度

        #存储对权重矩阵的梯度
        self.dw_ih_stack = []
        self.dw_hh_stack = []

        #存储对偏置的梯度
        self.db_ih_stack = []
        self.db_hh_stack = []

        self.prev_hidden_stack = [] #存储前一步的隐藏状态
        self.next_hidden_stack = [] #存储下一步的隐藏状态

        # temporary cache
        self.prev_dh = None #临时缓存上一步的梯度


    #接收当前的输入和前一步的隐藏状态，计算下一步的隐藏状态，并返回
    def __call__(self, x, prev_hidden):
        self.x_stack.append(x) #将输入添加到x_stack中

        #计算下一步的隐藏状态，通过激活函数tanh 到线性组合的权重和偏置上
        next_h = np.tanh(
            np.dot(x, self.weight_ih.T)
            + np.dot(prev_hidden, self.weight_hh.T)
            + self.bias_ih + self.bias_hh)

        #将前一步的隐藏状态和下一步的隐藏状态加到相应的堆栈中
        self.prev_hidden_stack.append(prev_hidden)
        self.next_hidden_stack.append(next_h)

        # clean cache 清空上一步的梯度缓存
        self.prev_dh = np.zeros(next_h.shape)
        return next_h

    #计算损失函数对权重的梯度
    def backward(self, dh):
        #从堆栈中取出当前的输入、前一步的隐藏状态和下一步的隐藏状态
        x = self.x_stack.pop()
        prev_hidden = self.prev_hidden_stack.pop()
        next_hidden = self.next_hidden_stack.pop()

        #使用链式法则，计算tanh激活函数的梯度
        #更新上一步的梯度缓存,计算对权重的梯度并存储到相应的堆栈中
        d_tanh = (dh + self.prev_dh) * (1 - next_hidden ** 2)
        self.prev_dh = np.dot(d_tanh, self.weight_hh)

        dx = np.dot(d_tanh, self.weight_ih)
        self.dx_list.insert(0, dx)

        dw_ih = np.dot(d_tanh.T, x)
        self.dw_ih_stack.append(dw_ih)

        dw_hh = np.dot(d_tanh.T, prev_hidden)
        self.dw_hh_stack.append(dw_hh)

        self.db_ih_stack.append(d_tanh)
        self.db_hh_stack.append(d_tanh)

        return self.dx_list


if __name__ == '__main__':
    #设置随机种子 为确保numpy和pytorch在生成随机数时得到相同的结果
    np.random.seed(123)
    torch.random.manual_seed(123)

    #设置numpy的打印选项、输出格式
    #precision设置小数点后保留位数 suppress=True表示打印小数时不显示末尾的零
    np.set_printoptions(precision=6, suppress=True)

    #使用pytorch定义RNN，输入特征数量为4，隐藏层单元数量为5 double确保使用双精度浮点数
    rnn_PyTorch = torch.nn.RNN(4, 5).double()

    #将pytorch的RNN权重转换为numpy格式，自定义numpy RNN
    rnn_numpy = RNNCell(rnn_PyTorch.all_weights[0][0].data.numpy(),
                        rnn_PyTorch.all_weights[0][1].data.numpy(),
                        rnn_PyTorch.all_weights[0][2].data.numpy(),
                        rnn_PyTorch.all_weights[0][3].data.numpy())

    nums = 3 #设置轮数

    # 生成随机输入、隐藏状态和梯度数据
    #输入数据
    x3_numpy = np.random.random((nums, 3, 4))
    x3_tensor = torch.tensor(x3_numpy, requires_grad=True)

    #初始隐藏状态
    h3_numpy = np.random.random((1, 3, 5))
    h3_tensor = torch.tensor(h3_numpy, requires_grad=True)

    #反向传播梯度
    dh_numpy = np.random.random((nums, 3, 5))
    dh_tensor = torch.tensor(dh_numpy, requires_grad=True)

    #使用pytorch的RNN进行前向传播
    h3_tensor = rnn_PyTorch(x3_tensor, h3_tensor)

    #使用自定义的numpy RNN进行前向传播
    h_numpy_list = []
    h_numpy = h3_numpy[0]

    #逐步将输入数据喂给numpy RNN,并收集每一步的输出隐藏状态
    for i in range(nums):
        h_numpy = rnn_numpy(x3_numpy[i], h_numpy)
        h_numpy_list.append(h_numpy)

    #pytorch RNN 进行反向传播
    h3_tensor[0].backward(dh_tensor)
    for i in reversed(range(nums)):
        rnn_numpy.backward(dh_numpy[i])

    #打印两个RNN的各类参数以及隐藏状态 进行比较
    print("numpy_hidden :\n", np.array(h_numpy_list))
    print("torch_hidden :\n", h3_tensor[0].data.numpy())
    print('=' * 20)

    print("dx_numpy :\n", np.array(rnn_numpy.dx_list))
    print("dx_torch :\n", x3_tensor.grad.data.numpy())
    print('=' * 20)

    print("dw_ih_numpy :\n",
          np.sum(rnn_numpy.dw_ih_stack, axis=0))
    print("dw_ih_torch :\n",
          rnn_PyTorch.all_weights[0][0].grad.data.numpy())
    print('=' * 20)

    print("dw_hh_numpy :\n",
          np.sum(rnn_numpy.dw_hh_stack, axis=0))
    print("dw_hh_torch :\n",
          rnn_PyTorch.all_weights[0][1].grad.data.numpy())
    print('=' * 20)

    print("db_ih_numpy :\n",
          np.sum(rnn_numpy.db_ih_stack, axis=(0, 1)))
    print("db_ih_torch :\n",
          rnn_PyTorch.all_weights[0][2].grad.data.numpy())


    print("db_hh_numpy :\n",
          np.sum(rnn_numpy.db_hh_stack, axis=(0, 1)))
    print("db_hh_torch :\n",
          rnn_PyTorch.all_weights[0][3].grad.data.numpy())

输出结果：

D:\Anaconda3\python.exe C:/Users/27513/PycharmProjects/pythonProject/main.py?
numpy_hidden :
?[[[ 0.4686 ? -0.298203 ?0.741399 -0.446474 ?0.019391]
? [ 0.365172 -0.361254 ?0.426838 -0.448951 ?0.331553]
? [ 0.589187 -0.188248 ?0.684941 -0.45859 ? 0.190099]]

?[[ 0.146213 -0.306517 ?0.297109 ?0.370957 -0.040084]
? [-0.009201 -0.365735 ?0.333659 ?0.486789 ?0.061897]
? [ 0.030064 -0.282985 ?0.42643 ? 0.025871 ?0.026388]]

?[[ 0.225432 -0.015057 ?0.116555 ?0.080901 ?0.260097]
? [ 0.368327 ?0.258664 ?0.357446 ?0.177961 ?0.55928 ]
? [ 0.103317 -0.029123 ?0.182535 ?0.216085 ?0.264766]]]
torch_hidden :
?[[[ 0.4686 ? -0.298203 ?0.741399 -0.446474 ?0.019391]
? [ 0.365172 -0.361254 ?0.426838 -0.448951 ?0.331553]
? [ 0.589187 -0.188248 ?0.684941 -0.45859 ? 0.190099]]

?[[ 0.146213 -0.306517 ?0.297109 ?0.370957 -0.040084]
? [-0.009201 -0.365735 ?0.333659 ?0.486789 ?0.061897]
? [ 0.030064 -0.282985 ?0.42643 ? 0.025871 ?0.026388]]

?[[ 0.225432 -0.015057 ?0.116555 ?0.080901 ?0.260097]
? [ 0.368327 ?0.258664 ?0.357446 ?0.177961 ?0.55928 ]
? [ 0.103317 -0.029123 ?0.182535 ?0.216085 ?0.264766]]]
====================
dx_numpy :
?[[[-0.643965 ?0.215931 -0.476378 ?0.072387]
? [-1.221727 ?0.221325 -0.757251 ?0.092991]
? [-0.59872 ?-0.065826 -0.390795 ?0.037424]]

?[[-0.537631 -0.303022 -0.364839 ?0.214627]
? [-0.815198 ?0.392338 -0.564135 ?0.217464]
? [-0.931365 -0.254144 -0.561227 ?0.164795]]

?[[-1.055966 ?0.249554 -0.623127 ?0.009784]
? [-0.45858 ? 0.108994 -0.240168 ?0.117779]
? [-0.957469 ?0.315386 -0.616814 ?0.205634]]]
dx_torch :
?[[[-0.643965 ?0.215931 -0.476378 ?0.072387]
? [-1.221727 ?0.221325 -0.757251 ?0.092991]
? [-0.59872 ?-0.065826 -0.390795 ?0.037424]]

?[[-0.537631 -0.303022 -0.364839 ?0.214627]
? [-0.815198 ?0.392338 -0.564135 ?0.217464]
? [-0.931365 -0.254144 -0.561227 ?0.164795]]

?[[-1.055966 ?0.249554 -0.623127 ?0.009784]
? [-0.45858 ? 0.108994 -0.240168 ?0.117779]
? [-0.957469 ?0.315386 -0.616814 ?0.205634]]]
====================
dw_ih_numpy :
?[[3.918335 2.958509 3.725173 4.157478]
?[1.261197 0.812825 1.10621 ?0.97753 ]
?[2.216469 1.718251 2.366936 2.324907]
?[3.85458 ?3.052212 3.643157 3.845696]
?[1.806807 1.50062 ?1.615917 1.521762]]
dw_ih_torch :
?[[3.918335 2.958509 3.725173 4.157478]
?[1.261197 0.812825 1.10621 ?0.97753 ]
?[2.216469 1.718251 2.366936 2.324907]
?[3.85458 ?3.052212 3.643157 3.845696]
?[1.806807 1.50062 ?1.615917 1.521762]]
====================
dw_hh_numpy :
?[[ 2.450078 ?0.243735 ?4.269672 ?0.577224 ?1.46911 ]
?[ 0.421015 ?0.372353 ?0.994656 ?0.962406 ?0.518992]
?[ 1.079054 ?0.042843 ?2.12169 ? 0.863083 ?0.757618]
?[ 2.225794 ?0.188735 ?3.682347 ?0.934932 ?0.955984]
?[ 0.660546 -0.321076 ?1.554888 ?0.833449 ?0.605201]]
dw_hh_torch :
?[[ 2.450078 ?0.243735 ?4.269672 ?0.577224 ?1.46911 ]
?[ 0.421015 ?0.372353 ?0.994656 ?0.962406 ?0.518992]
?[ 1.079054 ?0.042843 ?2.12169 ? 0.863083 ?0.757618]
?[ 2.225794 ?0.188735 ?3.682347 ?0.934932 ?0.955984]
?[ 0.660546 -0.321076 ?1.554888 ?0.833449 ?0.605201]]
====================
db_ih_numpy :
?[7.568411 2.175445 4.335336 6.820628 3.51003 ]
db_ih_torch :
?[7.568411 2.175445 4.335336 6.820628 3.51003 ]
db_hh_numpy :
?[7.568411 2.175445 4.335336 6.820628 3.51003 ]
db_hh_torch :
?[7.568411 2.175445 4.335336 6.820628 3.51003 ]

Process finished with exit code 0

我认为最大的难点就是链式法则公式和矩阵形状的设定，链式法则的思想简单，但是书写出来很容易出现细节性错误，尤其是循环神经网络的参数相对较多，还要注意上下层的角标；矩阵形状的设定也容易写错，稍微不注意就报错了，显示形状不匹配...只能多尝试细心点。

“学习”的最初阶段就是模仿与借鉴，这段代码参考了上一届学长们的博客，我捋顺了思路，画出了流程图，再加上手推了一遍BPTT算法(虽然对邱老师书中得到的某些公式没有理解透彻，但是我听了老师的建议，先把难理解的公式背了下来)，这段代码很好理解，毕竟BPTT与前馈神经网络的反向传播(BP)有异曲同工之妙，步骤和思想都很类似。

顺便复习一下tanh激活函数的性质

期末考试临近，想复习其他的激活函数性质可以看以下这几篇大佬的博客，总结得非常全面：

详解激活函数（Sigmoid/Tanh/ReLU/Leaky ReLu等） - 知乎 (zhihu.com)

激活函数Tanh_tanh激活函数-CSDN博客

深度学习笔记：如何理解激活函数？（附常用激活函数） - 知乎 (zhihu.com)

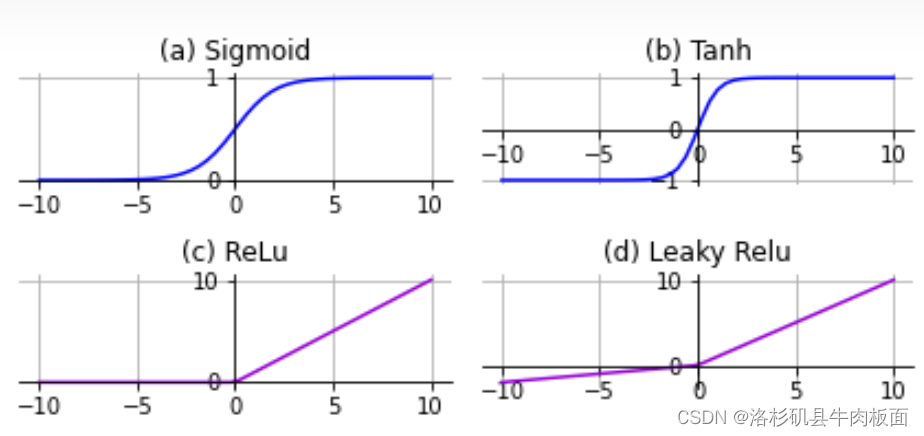
Tanh 激活函数又叫双曲正切激活函数（hyperbolic tangent activation function）。 Tanh 函数将其压缩至[-1,1]的区间内,输出以零为中心。

tanh计算公式与导数：

$y=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$

$\frac{dy}{dx}=1-y^{2}$

图像：

下图是我们目前阶段常用的几类激活函数的图像：

文章来源:https://blog.csdn.net/weixin_63010525/article/details/134833828
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！

NNDL 作业10 BPTT [HBU]

习题6-1P 推导RNN反向传播算法BPTT.

习题6-2 推导公式(6.40)和公式(6.41)中的梯度．

习题6-3 当使用公式(6.50)作为循环神经网络的状态更新公式时， 分析其可能存在梯度爆炸的原因并给出解决方法．

没理解的部分：

习题6-2P 设计简单RNN模型，分别用Numpy、Pytorch实现反向传播算子，并代入数值测试.

顺便复习一下tanh激活函数的性质

习题6-3 当使用公式(6.50)作为循环神经网络的状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决方法．