MIT_线性代数笔记：第 16 讲 投影矩阵和最小二乘法

投影 Projections

上一讲介绍了投影矩阵 P=A($A^T$A)${}^{?1}$$A^T$，当它作用于向量 b，相当于把 b 投影到矩阵 A 的列空间。

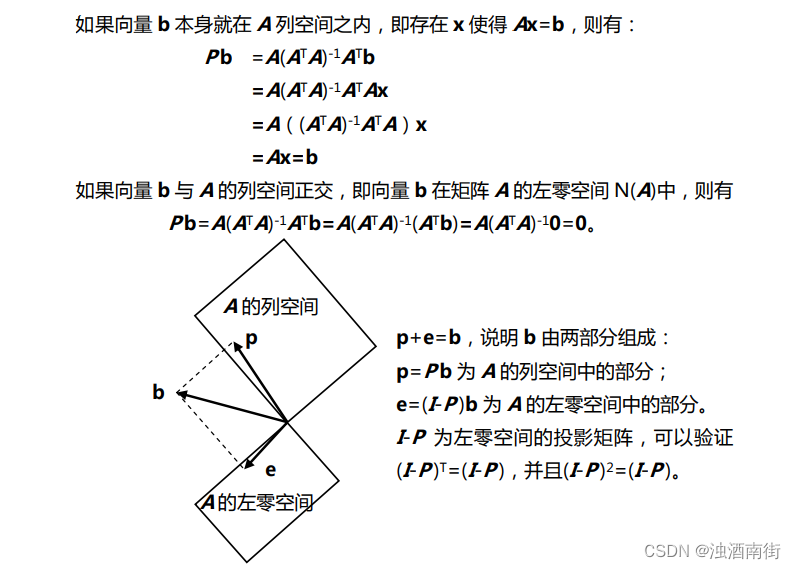
p+e=b,说明 b由两部分组成：
p =Pb为A 的列空间中的部分；
e = (I?P)b为A 的左零空间中的部分。
I ? P 为左零空间的投影矩阵，可以验证$(I?P{)}^T$ = ( I ? P )，并且$(I?P{)}^2$ =( I ? P )。

最小二乘法 Least Squares

应用投影矩阵求方程组最优解的方法，最常用于“最小二乘法”拟合曲线。

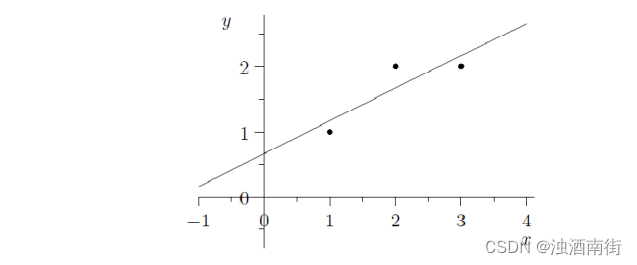
三个点{(1,1), (2,2), (3,2)}，求直线方程 b=C+Dt，要求直线尽量接近于三个点。
$$\begin{array}{r}C+D=1\\ C+2D=2\\ C+3D=2\end{array}矩阵形式为\left[\begin{array}{cc}1& 1\\ 1& 2\\ 1& 3\end{array}\right]\left[\begin{array}{c}C\\ D\end{array}\right]=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$
这个的方程 Ax=b 是无解的，解决办法就是求其最优解，最优解的含义即为误差最小，这里误差就是每个方程误差值的平方和
$${\Vert \begin{array}{c}e\end{array}\Vert }^2={\Vert \begin{array}{c}Ax?b\end{array}\Vert }^2$$ ，因此就是寻找具有最小误差平方和的解 x，这就是所谓的“最小二乘”问题。 其中最接近的解为将b投影到A矩阵的系数x。
$${\Vert \begin{array}{c}e\end{array}\Vert }^2={\Vert \begin{array}{c}Ax?b\end{array}\Vert }^2={\Vert \begin{array}{c}e1\end{array}\Vert }^2+{\Vert \begin{array}{c}e2\end{array}\Vert }^2+{\Vert \begin{array}{c}e3\end{array}\Vert }^2$$
误差即为数据点到直线距离的平方和。这部分工作可称为线性回归，在数据点中没有“离群值” 时，这是非常有用的方法。

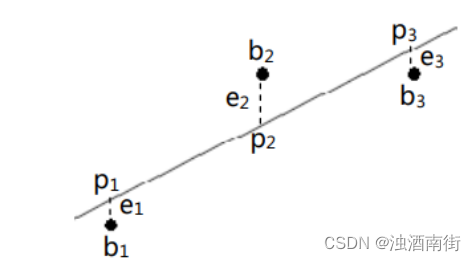
从几何上讨论求解过程，就是试图寻找数据点到直线距离的平方和 $e_1^2$ +$e_2^2$ +$e_3^2$ 最小的情况，此时得到的 C+Dt 分别为 p1，p2和 p3，它们是满足方程并最接近于 b的结果。另一种看法是，对于 R3空间上的向量 b，它投影到矩阵 A 的列空间中会得到向量 p=[p1 p2 p3]T，投影到矩阵 A 的零空间中则为 e。

投影向量p与误差向量e是正交的：

矩阵 $A^T$A